Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Фрактальный анализ и синергетика катализа в наносистемах

Нафадзокова Л. Х., Козлов Г. В.,

Глава 3. Физические основы катализа реакции переэтерификации соединениями металлов

В настоящем разделе будут вкратце рассмотрены закономерности катализа модельной реакции переэтерификации соединениями металлов на примере традиционного катализатора тетрабутоксититана (ТБТ), как в случае использования только ТБТ, так и его совместного применения с нанонаполнителем (слюдой). Авторы [1] выполнили сравнительный кинетический анализ реакции переэтерификации без катализатора и в присутствии ТБТ с содержанием последнего 0,10 мольных % в расчете на реагент, взятый в недостатке. Этот анализ выполнен в рамках современных физических концепций [2-4].

Кинетические кривые степень конверсии-продолжительность реакции Q-t для реакции переэтерификации без катализатора и в присутствии ТБТ показаны на рис. 3.1. Обращает на себя внимание как количественное, так и качественное различие приведенных на рис. 3.1 кривых Q(t). Количественное различие выражается в гораздо более быстром росте Q по мере увеличения t, обусловленном наличием катализатора, что и следовало ожидать. Качественное различие отражается в изменении формы кривой Q(t): если в отсутствии ТБТ (некатализируемой реакции переэтерификации) получена линейная зависимость, которая указывает на протекание реакции в евклидовом (однородном) пространстве [5], то в присутствии ТБТ получена типичная криволинейная зависимость Q(t) c уменьшением скорости реакции dQ/dt по мере роста t. Такие реакции типичны для неоднородных (фрактальных) сред [8], вследствие чего они названы фракталоподобными. Зависимость dQ/dt от t в этом случае описывается соотношением (2.15), в котором показатель гетерогенности среды h варьируется в пределах 0<h≤1 для фрактальных сред и равен нулю для гамогенной (евклидовой) среды [6]. В последнем случае dQ/dt=const и зависимость Q(t) линейна, что и наблюдается для реакции переэтерификации без катализатора (рис. 3.1).

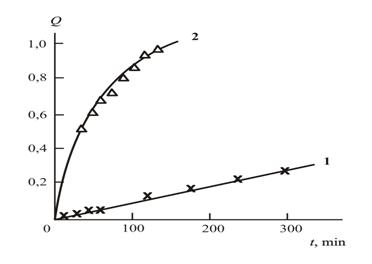
Рис. 3.1. Кинетические кривые степень конверсии–продолжительность реакции Q-t для реакции переэтерификации без катализатора (1) и в присутствии ТБТ(2)[1].

Рассмотрим причины фракталоподобной реакции переэтерификации в присутствии ТБТ. Эту реакцию, в общем, виде можно описать как реакцию рекомбинации реагентов А и В [4]:

А+В→ инертный продукт    (3.1)

В рамках теории среднего поля спад концентрации реагента Аρ_А при условии ρ_А= ρ_В дается уравнением [4]:

,    (3.2)

где k₁-константа скорости первого порядка.

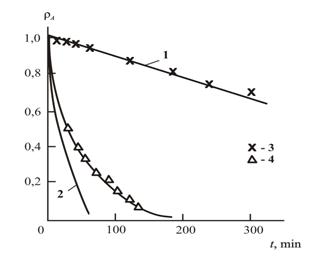
Рис.3.2. Зависимости спада концентрации реагента Аρ_А от продолжительности реакции t для реакции переэтерификации без катализатора (1,3) и в присутствии ТБТ(2,4). 1,2–расчет по соотношению (3.2); 3,4– экспериментальные данные[1].

На рис. 3.2 приведено сравнение рассчитанных по соотношению (3.2) и полученных экспериментально функций ρ_А(t), где ρ_А определена как (1-Q). Как можно видеть, для реакции переэтерификации без катализатора спад ρ_А по мере роста t превосходно описывается в рамках теории среднего поля, тогда как в присутствии ТБТ спад ρ_А гораздо более медленный, чем предсказывает соотношение (3.2). Как известно [4], последний эффект обусловлен локальными флуктуациями распределения реагентов и в этом случае функция ρ_А(t) дается следующим образом:

ρ_А(t) ~ t^-α ,  (3.3)

и

ρ_А(t) ~ ехр(-At^-α),   (3.4)

для малых и больших времен реакции, соответственно. В соотношениях (3.3) и (3.4) показатель α определяется размерностью пространства d, в котором протекает реакция, А- константа.

Для реакции рекомбинации описываемой уравнением (3.1), можно записать [4]:

.  (3.5)

Отметим три важных аспекта, вытекающих из применения модели [4] для описания реакции переэтерификации. Во-первых, поскольку реакция переэтерификации с ТБТ и в его отсутствие протекают в идентичных условиях, то из сравнения кинетических кривых рис. 3.1 следует, что фракталоподобное поведение реакции в присутствии ТБТ обусловлено локальными флуктуациями распределения катализатора в реакционной среде. Во-вторых, деление продолжительности реакции на малые и большие времена связана с диффузией реагентов и катализатора [4]. При наличии локальных флуктуаций существуют достаточно малые области размером ξ, где положительные или отрицательные (т.е., избыток или недостаток) флуктуации ТБТ достаточно велики. Если мы получим характеристический масштаб времени t_ξ, которое требуется для прохождения диффундирующей частицей расстояния ξ, то условие t< t_ξ дает малые времена, а t>t_ξ – большие. И, в третьих, уравнение (3.5) дает величину показателя α для свободной диффузии реагентов. В случае принудительной (с преимущественной ориентацией) диффузии величина α определяется следующим образом [4]:

,  (3.6)

т.е., для трехмерного пространства в случае принудительной диффузии α=1. В этом случае скейлинговый подход [4] дает соотношение (3.3), аналогичное уравнению (3.2). Это соответствие подтверждается данными рис. 3.2. Таким образом, указанный результат позволяет сделать вывод, что интенсивное перемешивание реакционной среды приводит к принудительной диффузии реагентов (метилбензоата и гептанола-1), но диффузия ТБТ остается свободной.

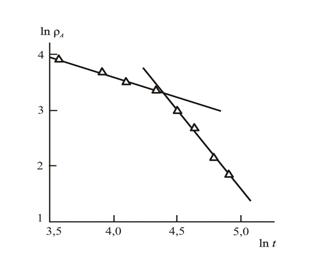
Рис.3.3. Зависимость спада концентрации реагента Аρ_А от продолжительности реакции t в двойных логарифмических координатах для реакции переэтерификации в присутствии ТБТ[1].

На рис. 3.3 приведена зависимость ρ_А(t) в двойных логарифмических координатах, соответствующая соотношению (3.3), для реакции переэтерификации в присутствии ТБТ. Как можно видеть, эта зависимость распадается на два линейных участка с разными наклонами. Для первого участка (t<90 мин.) наклон равен ~0,75, т.е., соответствует уравнению (3.5) для протекания реакции в трехмерном евклидовом пространстве (d=3). Для второго участка (t>90 мин.) наклон равен ~3, т.е., не согласуется с возможными значениями этого показателя для реакции рекомбинации или других аналогичных реакций, для которых значение α ограничено сверху величиной 1,5 [2-4,7]. Это означает, что для рассматриваемой реакции переэтерификации времена меньше 90 мин. идентифицировать как малые, т.е., на этом временном интервале спад концентрации реагирующих частиц контролируется локальными флуктуациями распределения ТБТ, а времена, равные или больше 90 мин. - к большим, где ТБТ распределен равномерно. Это означает, что в последнем случае функция ρ_А(t) должна описываться соотношением (3.4). Действительно, приведенная на рис. 3.4 зависимость ρ_А от t^d/4 в логарифмических координатах является линейной, что подтверждает сделанное выше предположение.

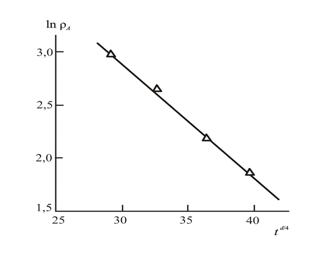
Рис.3.4. Зависимость спада концентрации реагента Аρ_А от параметра t^d/4(d=3) в логарифмических координатах в случае больших времен для реакции переэтерификации в присутствии ТБТ[1].

Следовательно, реакция переэтерификации без катализатора может быть описана в приближении среднего поля, тогда как введение катализатора (ТБТ) определяет появление локальных флуктуаций ТБТ. Этот эффект приводит к фракталоподобной кинетике реакции переэтерификации. В этом случае реакция переэтерификации рассматривается как реакция рекомбинации и трактуется в рамках скейлинговых подходов. Практический аспект данного исследования очевиден – гомогенное распределение катализатора в реакционной среде или его принудительная диффузия позволяет уменьшить продолжительность реакции примерно в два раза [1].

Наиболее интересной особенностью реакции переэтерификации в присутствии 0,02 и 0,10 моль.% ТБТ является то, что увеличение концентрации катализатора в 5 раз практически не изменяет кинетику реакции и при малых временах величина Q для обеих концентраций ТБТ определяется одним общим уравнением [8]:

Q = 1-7,1t^-d/4,  (3.7)

где t дается в минутах, а d=3.

Следовательно, основным фактором, определяющим кинетику реакции переэтерификации в присутствии ТБТ, является не содержание катализатора, а его локальные флуктуации, увеличивающие продолжительность реакции в 2¸3 раза [8].

Как показано выше, введение 0,10 моль.% ТБТ резко ускоряет реакцию переэтерификации (константа скорости реакции k₁ увеличивается более чем на порядок-от 0,18х10^-4с^-1 до 0,32 х10^-3с^-1), а также приводит к изменению типа кривой Q(t) от линейной к криволинейной (фракталоподобной, см. рис. 3.1). Расчет по соотношению (2.15) для реакции переэтерификации в присутствии ТБТ дал величину h=0,52. В свою очередь эффективная спектральная размерность  реакционной среды определяется так [9]:

=2 (1-h).   (3.8)

Таким образом, для реакции переэтерификации без катализатора (h=0, классический случай [6]) =2,0, а при введении ТБТ ее величина снижается до =0,96 [10]. Это означает изменение степени связанности реакционной среды или появление в ней своего рода пустот, т.е., областей без катализатора. Величину  можно рассматривать как число взаимно ортогональных направлений на фрактальном множестве или дробное число степеней свободы [11]. Следовательно, введение ТБТ уменьшает указанные выше параметры примерно в два раза.

Количественное описание кинетики реакции переэтерификации можно получить с помощью следующего уравнения [12]:

Q=Аt^/2,      (3.9)

где А-константа, пропорциональная числу мест реакции.

Уравнение (3.9) хорошо описывает кривые Q(t) при следующих значениях его параметров: реакция переэтерификации без катализатора =2,0 и А=9,2х10^-4 и для реакции в присутствии ТБТ =0,96 и А=9,2х10^-2. Таким образом, введение ТБТ приводит к появлению существенной неоднородности (гетерогенности) реакционной среды (рост h) и соответствующему снижению степени ее эффективной связности, характеризуемой размерностью , а также к увеличению числа мест реакции, характеризуемого параметром А [10].

Следующим очевидным этапом этого раздела является исследование влияния нанонаполнителя (слюды) на кинетику реакции переэтерификации в присутствии катализатора (ТБТ), которое было выполнено в работе [13].

 На рис.3.5 сплошными линиями показаны экспериментальные кинетические кривые степень конверсии – продолжительность реакции Q(t) для трех реакций переэтерификации с необработанной слюдой, с ТБТ и совместным присутствием слюды и ТБТ. Как можно видеть, скорость реакции возрастает именно в таком порядке (константы скорости реакции k₁ равны 0,15х10^-4, 3,15х10^-4 и 3,90х10^-4 с^-1, соответственно). Если реакция переэтерификации без катализатора (ТБТ) имеет линейную кинетику Q(t) и, следовательно, моделируется в рамках теории среднего поля (см. уравнение (3.2)), то реакции в присутствии ТБТ имеют криволинейную кинетику, в которой спад концентрации реагентов более медленный по сравнению с линейным (см. рис. 3.2). Как показано выше, указанная криволинейность определяется гетерогенностью (фрактальностью) реакционной среды [6,9], обусловленной локальными флуктуациями распределения ТБТ [1,8,10].

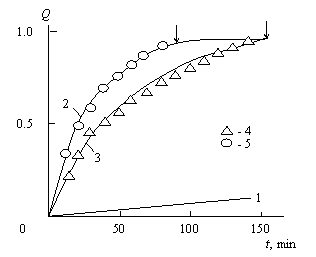
Рис.3.5. Экспериментальные (сплошные линии) и рассчитанные согласно уравнению (3.10) (точки) кинетические кривые Q(t) для реакции переэтерификации со слюдой (1), ТБТ (2, 4), слюдой и ТБТ (3, 5). [13].

На рис. 3.6 приведены зависимости ρ_А(t) в двойных логарифмических координатах, соответствующие соотношению (3.3). Как следует из этих графиков, при малых временах для реакций с ТБТ, как и выше, получены разные наклоны: для реакции без слюды α=0,75 или d/4, в присутствии слюды α=1,0 или (d+1)/4.

Рис.3.6. Зависимости ρ_А(t) в двойных логарифмических координатах, соответствующие соотношению (3.3), для реакции переэтерификации с ТБТ (1), со слюдой и ТБТ (2) [13].

Таким образом, интенсивное перемешивание реакционной среды вызывает принудительную диффузию ТБТ только в присутствии слюды. Этот эффект существенно ускоряет реакцию переэтерификации.

При больших временах реакция переэтерификации описывается соотношением (3.4) с α=0,75 или d/4 (см. рис. 3.4). Иначе говоря, в случае, когда большая часть ТБТ израсходована, перемешивание реакционной среды уже не может вызвать принудительную диффузию и обе реакции (со слюдой и без нее) описываются соотношением (3.4) с α= d/4, но с разными значениями коэффициента А.

Для объяснения перехода от свободной диффузии к принудительной в катализируемой реакции переэтерификации авторы [13] использовали фрактальную модель кинетики химических реакций [14,15]. Основное уравнение этой модели имеет вид [13]:

Q = C_oh_ot^(3-D_f ^)/2 ,       (3.10)

C_o - начальная концентрация реагентов, h_o - исходная вязкость реакционной среды, D_f - фрактальная размерность продукта реакции.

Отметим важный с точки зрения фракталов момент. Продукт модельной реакции переэтерификации (молекулу гептилбензоата) нельзя рассматривать как фрактальный объект в строгом физическом смысле этого термина, поскольку она, в отличие от макромолекулярного клубка [16], не обладает свойством самоподобия. Тем не менее, как отмечалось выше [17], в процессе переэтерификации кривая Q(t) имеет автозамедленный характер, а это означает, что молекула гептилбензоата ведет себя подобно фрактальному объекту и в силу указанных обстоятельств названа, следуя Копельману [6], фрактальноподобным объектом [18].

Из уравнения (3.10) следует, что построение зависимостей Q(t) в двойных логарифмических координатах в случае линейности этих зависимостей позволяет получить из их наклона величину D_f фракталоподобной молекулы гептилбензоата. Такие зависимости приведены на рис. 3.7, они действительно линейны и по их наклону была определена величина D_f=2,02, одинаковая в случае катализируемых ТБТ реакций переэтерификации как в присутствии слюды, так и без нее. Это означает, что разная форма кривых Q(t) для указанных реакций не является следствием разной структуры продукта реакции.

Достаточно очевидно, что введение слюды в реакционную смесь должно повысить ее вязкость η₀. Теоретическую оценку степени такого повышения η₀ можно выполнить в рамках модели Кернера, из которой для суспензий следует [19]:

,     (3.11)

где  и ₀ – исходные вязкости реакционной среды в присутствии слюды и без нее, соответственноφ_н –объемная доля наполнител(слюды).

Рис. 3.7. Зависимость Q(t) в двойных логарифмических координатах соответствующих уравнению (3.10), для реакции переэтерификации с ТБТ (1), слюдой и ТБТ (2) [13].

Если в качестве первого приближения принять равными объемную и массовые доли наполнителя, то уравнение (3.11) даст увеличение  реакционной среды в присутствии слюды по сравнению с η₀ в 2,07 раза.

Далее, пологая в уравнении (3.10) величину с₀=1,0 для реакционной среды без слюды и с₀=0,7 для этой же среды в присутствии слюды, можно рассчитать величины η₀ и  в относительных единицах, которые равны 0,084 и 0,157, соответственно. Таким образом, эта оценка, дает /₀=1,88, что близко к полученной согласно уравнению (3.11). Следовательно, приведенные выше результаты показали, что переход от свободной диффузии в случае реакционной среды без наполнителя к принудительной диффузии в присутствии слюды обусловлен увеличением исходной вязкости ₀, что позволяет захват частиц ТБТ при перемешивании.

Отметим еще один важный аспект. Для реакции переэтерификации в присутствии слюды без катализатора величина D_f=1,71 [17,20]. Это означает, что молекула гептилбензоата «растягивается» на поверхности слюды [21], что приводит к снижению D_f по сравнению с данными, полученными согласно рис. 3.7 (D_f=2,02). Это наблюдение предполагает, что введение ТБТ переносит реакцию с поверхности слюды в объем реакционной смеси, одновременно внося флуктуации в процесс переэтерификации (сравните кривые 1, 2 и 3 рис. 3.5).

Кинетические кривые Q(t) можно моделировать с помощью уравнения (3.10). На рис. 3.5 приведены результаты такого моделирования при следующих параметрах: для катализируемой реакции без слюды с₀=1,0, ₀=0,084 и D_f=2,02 и для этой же реакции переэтерификации в присутствии слюды с₀=0,7 (с учетом занимаемого слюдой объема), =0,157 и D_f=2,02. Как можно видеть, кинетические кривые Q(t) в обоих указанных случаях хорошо моделируется в рамках фрактальной кинетики химических реакций. Далее можно теоретически оценить время завершения реакции переэтерификации t_пр, полагая в уравнении (3.10) Q=1,0. На рис. 3.5 величины t_пр (равные 90 и 145 мин. для реакций в присутствии слюды и без нее, соответственно) указаны стрелками. Из данных рис. 3.5 следует, что эта оценка также хорошо соответствует экспериментальным результатом.

Следовательно, изложенные выше результаты предполагают, что увеличение скорости, катализируемой ТБТ реакции переэтерификации в присутствии нанонаполнителя (слюды) обусловлено переходом от свободной диффузии катализатора в отсутствии слюды к принудительной диффузии. Этот переход определяется увеличением исходной вязкости реакционной среды из-за присутствия нанонаполнителя. Указанный эффект позволяет снизить продолжительность реакции переэтерификации примерно в 1,6 раза [22].

И в заключение настоящей главы рассмотрим кинетику реакции переэтерификации в случае, когда ТБТ был нанесен на поверхность слюды, обработанной серной кислотой (СМК) [23]. На рис. 3.8 приведены кинетические кривые степень конверсии -продолжительность реакции Q(t) для всех пяти исследованных в настоящей главе типов реакции переэтерификации. Как отмечалось в главе 2, все эти реакции моделировались в рамках кинетики реакций первого порядка. Как следует из данных рис. 3.8, кинетика этих реакций очень различается, о чем можно судить по величине константы скорости реакции первого порядка k₁: она варьируется от 0,18х10^-4 до 29х10^-4с^-1. Наименьшее значение k₁ имеет реакция переэтерификации без катализатора и нанонаполнителя, наибольшее - реакция в присутствии СМК, обработанной ТБТ. Таким образом, СМК действует как катализатор реакции переэтерификации (подробно см. главу 2), хотя и более слабый, чем ТБТ, а обработка слюды ТБТ дает синергический

эффект. Рассмотрим физические основы наблюдаемого эффекта. Как было показано выше, молекулу гептилбензоата можно рассматривать как фракталоподобный объект с размерностью D_f. В этом случае для описания реакции переэтерификации может быть использована модель диффузионно-ограниченной агрегации (ДОА), модифицированная с учетом наличия в реакционной среде многих мест протекания реакции, т.е., активных центров с концентрацией с_акт [24]. Согласно этой модели, величину с_акт можно оценить с помощью соотношения [24]:

,   (3.12)

где R_q-радиус инерции фракталоподобной молекулы гептилбензоата, с₀- концентрация частиц, формирующих кластер (гептилбензоата), т.е., концентрация реагентов.

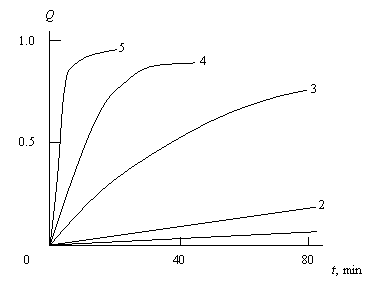
Рис.3.8. Кинетические кривые Q(t) для пяти типов реакции переэтерификации: 1-в отсутствии СМК и ТБТ; 2- в присутствии СМК, 3- в присутствии ТБТ; 4- в присутствии СМК и ТБТ; 5- в присутствии СМК обработанной ТБТ [23].

Поскольку гептилбензоат является низкомолекулярным веществом, для которого нет оснований ожидать роста молекулярной массы аналогично полимерам и, следовательно, увеличения R_q, то в работе [23] было принято R_q=сonst=10 относительных единиц. Во всех пяти исследуемых реакциях состав реагентов был одинаков и поэтому с₀= сonst. Определить величину размерности D_f можно с помощью уравнения (2.9), оценки согласно которому показали, что величина D_f для исследуемых реакций снижается от 1,95 до 1,13, а величина с_акт увеличивается от 1,1 до 7,4 относительных единиц. Другой способ описания реакции переэтерификации дает соотношение (2.10), в котором константа А пропорциональна числу захватов (объемов протекания реакции) [25].

Расчет по соотношению (2.10) показал, что величина А увеличивается по мере роста константы скорости реакции переэтерификации от 5 до 720 относительных единиц, т.е., она растет гораздо быстрее, чем с_акт. Получить линейную корреляцию между А и с_акт удалось только в форме кубической функции, т.е., А~ с³ _акт (рис. 3.9). Такая зависимость предполагает, что захватом является объем реакционной среды с радиусом R, равным [24]:

,      (3.13)

где d-размерность евклидова пространства, в котором протекает реакция, равная 3 в рассматриваемом случае, а согласно графику рис. 3.9 величина А может быть определена как R^-1 [23].

Рис.3.9. Соотношение между числом захватов А и активных мест с_акт для пяти исследуемых типов реакции переэтерификации [23].

На рис. 3.10 приведена зависимость k₁ от с_акт, которую вновь можно линеаризовать только в форме кубической функции. Исходя из сказанного выше, график рис. 3.10 предполагает, что реакция протекает в объеме, пропорциональном = и чем больше с_акт, тем меньше этот объем, тем больше вероятность реакции (тем больше число захватов реагентов).

Рис. 3.10. Зависимость константы скорости первого порядка k₁ от числа активных мест с_акт для пяти типов исследуемых реакций переэтерификации [23].

Следовательно, увеличение числа активных центров реакции приводит к снижению локального объема реакционной среды, в котором эта реакция может быть реализована. По своему физическому смыслу это означает ослабление пространственной флуктуации, что приводит к существенному росту скорости реакции переэтерификации. Очевидно, что с практической точки зрения наиболее выгодна реакция, катализируемая обработанной тетрабутоксититаном слюдой СМК[23].

И в заключение настоящей главы рассмотрим процесс катализа боридом молибдена Мо₂В в реакции жидкофазного эпоксидирования этилаллилэтилакрилата (ЭАЭА) гидропероксидом трет-бутила (ГПТБ). В указанной реакции наблюдается нелинейная зависимость начальной скорости эпоксидирования Wо от содержания катализатора [кат.] [26]. Такой эффект был объяснен уменьшением степени редиспергирования агрегатов Мо₂В по мере роста [кат.] в реакционной среде и соответствующим уменьшением доступной для катализа площади поверхности агрегатов Мо₂В. Тем не менее, авторы [26] признали, что в рассматриваемом ими случае этот эффект не может полностью объяснить полученные экспериментальные данные.

Известно, что используемые в настоящее время катализаторы имеют шероховатую поверхность, которая, как правило, является фрактальной [27-29]. Кроме того, как показано в работе [30], дисперсные порошки обладают фрактальной поверхностью частиц, чья размерность d_n изменяется в максимально широком диапазоне (2< d_n £ 3). Эти обстоятельства позволяют предположить, что поверхность Мо₂В также имеет фрактальную структуру.

Еще одним доводом в пользу такого предположения служит нелинейность зависимости W_o(кат), что является типичным признаком фрактальных реакций, т.е., либо реакций фрактальных объектов, либо реакций, протекающих во фрактальных пространствах [31,32]. Исходя из этого, авторы [33] продемонстрировали возможность количественного описания обнаруженных в работе [26] эффектов в рамках фрактального анализа.

Как известно [34], одним из наиболее примечательных свойств поверхности является ее способность контролировать физические и химические процессы относительно пути и скорости. Для диффузионно-контролируемых каталитических реакций в работе [34] получено следующее соотношение:

Q(t) ~ t ^(d-dn)/2,  (3.14)

где Q - число частиц, прореагировавших на поверхности катализатора или степень конверсии, t - продолжительность реакции, d - размерность евклидова пространства, в котором протекает реакция (очевидно в рассматриваемом случае d = 3), d_n - размерность поверхности катализатора.

Как показано в работе [34], соотношение (3.14) является достаточно общим и может быть использовано для описания любой реакции контролируемой диффузией. Так, авторы [14] использовали это соотношение для описания реакции полимеризации в форме уравнения (3.10).

Дифференцируя уравнение (3.14) по времени и используя аналогию с уравнением (3.10), можно получить [33]:

W_o ([кат], t) ~ [кат] t ^(1-dn)/2,   (3.15)

поскольку при применении [кат] в силу его малой абсолютной величины сколько-нибудь значительного изменения h_о не ожидается.

Чтобы рассчитать величину W_o согласно соотношению (3.15), необходимо оценить фрактальную размерность d_n поверхности агрегатов исходных частиц Мо₂В независимым способом. Для этой цели было использовано соотношение [30,34]:

S_u ~ R ^d n -3,   (3.16)

где S_u - удельная площадь поверхности исходного порошка Мо₂В, равная 0,31м²/2 [26], R - радиус агрегатов частиц Мо₂В, принятый по данным [26], в интервале 1,4 ¸2,4 мкм при вариации [кат] = 0,5¸6,0 г/дм³.

Полагая для [кат] = 0,5 г/дм³ и соответствующей ей величине R = 1,4мкм d_n = 2,2 [27], получим константу пропорциональности в соотношении (3.16), что позволяет расчет d_n как функции [кат]. Эта зависимость приведена на рис.3.11 (сплошная линия), откуда следует быстрый рост d_n при небольших [кат] и выход на плато - для [кат]>4г/дм³. Такая форма зависимости d_n от концентрации исходного дисперсного материала является типичной и наблюдается для других условий агрегации, в частности, агрегации порошка графита с размером исходных частиц ~10 мкм в полимерных композитах [35], которая описывалась следующим эмпирическим уравнением:

, (3.17)

где d_о и R_o - фрактальная размерность поверхности и радиус частиц исходного порошка, соответственно.

Рис.3.11. Зависимость фрактальной размерности d_n поверхности агрегатов частиц катализатора Мо₂В от его содержания [кат], рассчитанные согласно соотношениям (3.16) (1), (3.17) (2) и (3,15) (3) [33].

На рис. 3.11 также приведен расчет d_n согласно уравнению (3.17) при d_n =2,08 и R_o = 1,4 мкм. Как можно видеть получено достаточно хорошее соответствие зависимостей d_n ([кат]), рассчитанных по уравнению (3.16) и (3.17), хотя величины d_о для них несколько различаются (d_о =2,20 и 2,08), соответственно.

Далее можно теоретически рассчитать величину W_o, используя соотношение (3.15). На рис. 3.12 приведено сравнение экспериментальных и рассчитанных указанным образом зависимостей W_o([кат]), где величины d_n были оценены согласно уравнениям (3.16) и (3.17). Как можно видеть при обоих способах оценкиd_n фрактальная модель катализа [34] дает достаточно точное как качественное, так и количественное описание изменения W_o при вариации содержания катализатора Мо₂В. Иначе говоря, модель [34] дает корректное объяснение описанному в работе [26] эффекту. Как следует из соотношения (3.15), приd_n=2 (гладкая поверхность катализатора) зависимость W_o от [кат] будет линейной при t = const (кривая 1 на рис. 3.12), но W_o при [кат] = const является функцией времени, снижаясь по мере роста t. При d_n = 1 зависимость W_o от [кат] также будет линейной и не будет зависеть от t [33].

Используя соотношение (3.15), можно выполнить и обратную процедуру - рассчитать d_n по W_o, вновь полагая d_n = 2,2 при [кат] = 0,5 г/дм³ . Сравнение зависимостей d_n ([кат]), рассчитанных согласно соотношениям (3.15) и (3.16), показано на рис 3.11. Несмотря на определенные расхождения, и ход этих зависимостей, и абсолютные величины d_n достаточно хорошо согласуются (расхождение меньше 10%). Это обстоятельство указывает, что на начальной стадии катализа "отравления" катализатора не происходит [34]. Если бы такой эффект имел место, то полученные согласно соотношению (3.15) значения d_n были бы меньше соответствующих величин, рассчитанных из соотношения (3.16) [34].

Далее рассмотрим природу частиц катализатора. Как известно [26], плотность r этих агрегатов можно определить из соотношения:

.  (3.18)

Расчет r по уравнению (3.18) при S_n. = 0,31 м²/г = const и R = 1,4¸2,4 мкм показал снижение r по мере роста R в пределах 6910¸4030 кг/м³. Как известно [26], плотность частиц исходного катализатора Мо₂В r_о равна 9260 кг/м³. Таким образом, для агрегатов частиц выполняется условие r < r_о, что типично для рыхлых фрактальных агрегатов плотность которых определяется уравнением (1.33). Расчет согласно этому уравнению показал, что фрактальная размерность агрегатов частиц Мо₂В d_f в интервале R =1,4¸2,4 мкм изменяется незначительно, а именно в пределах d_f =2,13¸2,05. Отметим, что такая величина d_f типична для агрегатов, перестраивающихся во время процесса роста, т.е., включающих процессы реструктуризации [36].

Рис. 3.12. Зависимость начальной скорости эпоксидирования W_o от содержания катализатора [кат]: экспериментальные данные (1), расчет согласно соотношению (3.15) при d_n, определенной по уравнениям (3.16) (2) и (3.17) (3) и при d_n = 2 (4). ([ЭАЭА]о = 2,2 моль/л, [ГПТБ]о = 0,52 моль/л), Т=383К[26])[33].

Это указывает, что увеличение d_n по мере роста [кат] (см. рис 3.11) обусловлено только процессом агрегации исходных частиц катализатора. Эта величина d_f также хорошо согласуется с размерностью агрегатов частиц никеля, полученной экспериментально [37].

И, наконец, выясним физический смысл структурного фактора катализатора, контролирующего скорость эпоксидирования. Процесс катализа можно рассматривать как процесс роста фрактального объекта с той разницей, что вместо частиц, присоединяющихся к фрактальному объекту, мы будем учитывать реагирующие молекулы. Согласно [38], полагаем, что агрегат частиц катализатора радиусом Rимеет три типа мест:

1) уже посещенные молекулами ("зараженные" или "мертвые") места, принадлежащие кластеру;

2) уже посещенные, но заблокированные ("невосприимчивые") места;

3) еще не посещенные места, являющиеся соседями посещенных (места роста).

Узлы роста образуют "открытую границу" фрактала [39] и их множество Ng имеет фрактальную размерность d_g:

N_g ~ R ^dg .    (3.19)

Между массой кластера (агрегата) N и Ng существует следующее соотношение [38]:

N_g ~ N^х,     (3.20)

где х = d_g / d_f= 1/2. Поскольку N ~ R ^d_f, то из соотношений (3.19) и (3.20) получим [33]:

N_g ~ N ^dg/d_f ~ R ^d_f ^d_f/^d_f ~R ^dg ~ R ^df/2. (3.21)

Как показано выше, d_f »2 и тогда W_o ~ Ng ~ R. Этот вывод подтверждается данными рис. 3.13, где приведена зависимость W_o( R).

Следовательно, изложенные выше результаты показали, что методы фрактального анализа качественно и количественно объясняют полученный авторами [26] нелинейный характер зависимости начальной скорости эпоксидирования от содержания катализатора. Отметим, что континуальные модели, использующие представления евклидовой геометрии, не позволяют получить адекватного объяснения.

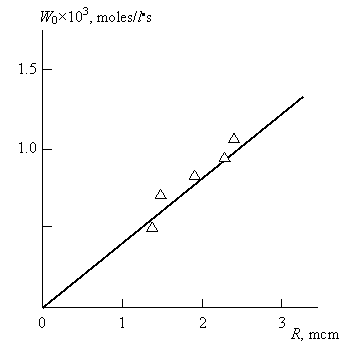
Рис.3.13. Зависимость начальной скорости эпоксидирования W_o от радиуса агрегатов частиц катализатора Мо₂В R [33].

Литература к Главе 3.

1. Naphadzokova L. Kh., Kozlov G.V., Zaikov G.E. In book: Monomer and Polymer Research Frontiers. Ed. D’Amore A., Zaikov G.E. New York, Nova Science Publishers, Inc., 2006, p. 69-75.

2. Grassberger P., Procaccia I. J.Chem. Phys., 1982, v. 77, № 12, p. 6281-6284.

3. Meakin P., Stanley H.E. J. Phys. A, 1984, v. 17, № 1, p. L173-L177.

4. Kang K., Redner S. Phys. Rev. Lett., 1984, v. 52, № 12, p. 955-958.

5. Козлов Г.В., Заиков Г.Е. Теоретические основы химической технологии, 2003, т. 37, № 5, с. 555-557.

6. Копельман Р.В. В кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 524-527.

7. Redner S., Kang K. J. Phys. A, 1984, v. 17, № 2, p. L451-L459.

8. Нафадзокова Л.Х., Овчаренко Е.Н., Козлов Г.В. Фундаментальные исследования, 2006, № 4, с. 101-102.

9. 9.Klymko P.W., Kopelman R. J. Phys. Chem., 1983, v. 87, № 23, p. 4565-4567.

10. Нафадзокова Л.Х., Гринева Л.Г., Козлов Г.В. Обозрение прикладной и промышленной математики, 2006, т. 13, № 1, с. 126-127.

11. Зеленый Л.М., Милованов А.В. Успехи физических наук, 2004, т. 174, № 8, с. 809-852.

12. Kozlov G.V., Zaikov G.E. The Structural Stabilization of Polymers: Fractal Models. Leiden-Boston, Brill Academic Publishers, 2006, 345 p.

13. Нафадзокова Л.Х., Козлов Г.В., Заиков Г.Е. Конструкции из композиционных материалов, 2008, №1, с.71-75.

14. Новиков В.У., Козлов Г.В., Успехи химии, 2000, т. 69, № 4, с. 378-399.

15. Kozlov G.V., Shustov G.B., Zaikov G.E. J. Balkan Tribologic. Assoc., 2003, v. 9, № 4, p. 467-514.

16. Havlin S., Ben-Avraham D. Phys. Rev. A, 1982, v. 26, № 3, p. 1728-1734.

17. Нафадзокова Л.Х., Карданов Х.М., Козлов Г.В. В сборн. научн. трудов «Седьмой регион. Наука и практика». Нальчик, Полиграфсервис т Т, 2005, с. 84-90.

18. Козлов Г.В., Нафадзокова Л.Х. Известия ВУЗов, Северо-Кавказск. регион, естествен. науки, 2006, № 3, с. 36-39.

19. Mills N.J. J.Appl. Polymer Sci., 1971, v. 15, № 11, p. 2791-2805.

20. Нафадзокова Л.Х., Козлов Г.В., Тленкопачев М.А. В сборн. статей VI Междунар. междисциплинарн. симпозиума «Фракталы и прикладная синергетика, ФиПС-2005». М., Интерконтакт Наука, 2005, с. 115-118.

21. Пфейфер П. В кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 72-81.

22. Нафадзокова Л.Х., Козлов Г.В., Шустов Г.Б. Матер. междунар. конф. «Органическая химия от Бутлерова и Бейльштейна до современности». СПб., 26-29 июня, 2006, с. 614-615.

23. Буря А.И., Нафадзокова Л.Х., Козлов Г.В., Жукова А.И. Вопросы химии и химической технологии, 2007, №2, с.73-75.

24. Witten T.A., Meakin P. Phys. Rev. B, 1983, v. 28, № 10, p. 5632-5642.

25. Джорджевич З. В кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 581-585.

26. Комаренская З.М., Никипанчук М.В., Трач Ю.Б., Яремко З.М., Федушинская Л.Б. Вопросы химии и химической технологии, 2002, № 1, с. 38-41.

27. Farin D., Peleg S., Yavin D. Langmuir, 1985, v. 1, № 4, p. 399-407.

28. Meakin P. Chem. Phys. Lett., 1986, v.123, 1983, v. 28, № 5, p. 428-432.

29. Wellner E., Pojanski D., Ottolenghi M., Huppert D., Avnir D. J. Amer. Chem. Soc., 1987, v. 109, № 3, p. 575-578.

30. Avnir D., Farin D., Pfeifer P. Nature, 1984, v. 308, № 5959, p. 261-263.

31. Kozlov G.V., Zaikov G.E. J. Balkan Tribologic Assoc., 2004, v. 10, № 1, p. 1-30.

32. Kozlov G.V., Zaikov G.E. In book: Handbook of Polymer Research, v. 20, Ed. Pethrick A., Zaikov G. New York, Nova Science Publichers, Inc., 2006, p. 85-117.

33. Kozlov G.V., Afaunova Z.I., Zaikov G.E. In book: Theoretical and Practical Guide to Organic Physical Chemistry. Ed. Zaikov G., Kozlov G., Makitra R. New York, Nova Science Publichers, Inc., 2006, p. 21-27.

34. Pfeifer P., Avnir D., Farin D. J. Stat. Phys., 1984, v. 36, № 5/6, p. 699-716.

35. Kozlov G.V., Lipatov Yu.S. Composite Interfaces, 2002, v. 9, № 6, p. 509-527.

36. Kolb M. J. Phys. A, 1986, v. 19, № 5, p. L263-L268.

37. Шамурина М.В., Ролдугин В.И., Прямова Т.Д., Высоцкий В.В. Коллоидный журнал, 1994, т. 56, № 3, с. 451-454.

38. Стенли Х. В кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 463-477.

39. Rammal R., Toulouse G. J. Phys. Lett. (Paris), 1983, v. 44, № 1, p. L13-L22.