
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Глава 5. Фрактальные модели кинетики полимеризации в присутствии наполнителя
Анализ процессов полимеризации в присутствии наполнителя в принципе не отличается от такового для модели реакции переэтерификации [1]. В настоящей главе будет исследовано несколько важных аспектов такой полимеризации в основном на примере твердофазной имидизации.
Авторы [2] исследовали кинетику твердофазной имидизации полиамидной кислоты (ПАК) в присутствии наполнителя (Na+-монтмориллонита) и обнаружили существенное ускорение реакции как по мере роста температуры имидизации Ти в интервале 423÷523К, так и по мере увеличения содержания Na+- монтмориллонита Wс в интервале 0÷7 вес.%. В работе [2] был предложен возможный химический механизм действия Na+-монтмориллонита в качестве катализатора, предполагающий большую площадь поверхности контакта и, соответственно, большое число активных мест реакции, что способствует дегидратации и реакции замыкания имидного кольца. Эта модель носит предположительный и качественный характер. Однако в последнее время стало очевидным, что на кинетику химических реакций большое влияние могут оказывать чисто физические факторы, такие как связность реакционной среды [3] или структура макромолекулярного клубка [128], который во всех состояниях полимера (растворе, расплаве, конденсированной фазе) является фракталом [5,6]. Также хорошо известно [7], что описание фрактальных объектов корректно только в рамках фрактальной геометрии, а использование в таком случае евклидовой геометрии дает более или менее соответствующее реальности приближение. Исходя из сказанного выше, авторы [8,9] выполнили описание реакции твердофазной имидизации как в присутствии нанонаполнителя, так и без него в рамках структурных (фрактальных) моделей.
В общем и наиболее простом виде реакцию твердофазной имидизации можно представить уравнением [3]:
А+А→ инертный продукт, (5.1)
где А-реагент (ПАК).
Тогда для описания такой реакции используется следующее соотношение [3]:
![]() , (5.2)
, (5.2)
где ρА-концентрация непрореагировавшего реагента А, которая в дальнейшем будет принята равной (1-Q), t-продолжительность реакции, ds-спектральная размерность.
На рис. 5.1 приведены зависимости ρА=(1-Q) от t в двойных логарифмических координатах, соответствующие соотношению (5.2), для реакции имидизации без наполнителя при четырех температурах имидизации Ти =423, 473, 503 и 523К. Как следует из данных рис.5.1, все четыре приведенных графика линейны, что позволяет определить величину спектральной размерности ds. Оценки показали, что повышение температуры имидизации Ти в интервале 423÷523К приводит к увеличению ds от 0,42 до 1,68, т.е., к существенному росту степени связанности реакционной системы. На рис. 5.2 приведены аналогичные зависимости для разных содержаний Na+- монтмориллонита Wc при фиксированной Ти =473К.
Как можно видеть, введение наполнителя оказывает гораздо более слабое влияние на величину ds, чем повышение температуры имидизации [9].
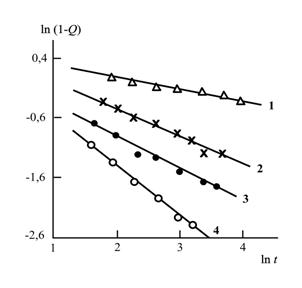
Рис.5.1. Зависимости ρА=(1-Q) от t в двойных логарифмических координатах, соответствующие соотношению (5.2) для твердой имидизации без наполнителя при температуре: 423 (1), 473 (2), 503 (3) и 523 (4) [8].
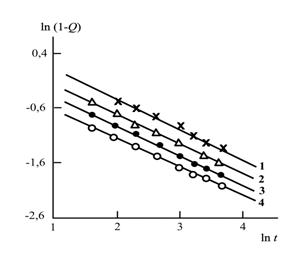
Рис.5.2. Зависимости ρА=(1-Q) от t в двойных логарифмических коор-динатах, соответствующие соот-ношению (5.2), для твердой имидизации без наполнителя при температуре 473 и содержании Na+-монтмориллонита Wс: 0(1), 2(2), 5(3) и 7(4) вес.% [8].
Увеличение ds по мере роста Ти для одной и той же реакционной системы, показанное на рис.5.1, предполагает, что в данном случае dsследует рассматривать как эффективную спектральную размерность ![]() , зависящую от степени неоднородности (гетерогенности) реакционной среды [10]. Степень неоднородности среды можно охарактеризовать показателем неоднородности (гетерогенности) h, который изменяется в пределах 0<h≤1 и обращается в нуль только для однородных систем [10]. Величины h и
, зависящую от степени неоднородности (гетерогенности) реакционной среды [10]. Степень неоднородности среды можно охарактеризовать показателем неоднородности (гетерогенности) h, который изменяется в пределах 0<h≤1 и обращается в нуль только для однородных систем [10]. Величины h и ![]() связаны между собой уравнением (3.18). На рис. 5.3 приведена зависимость h(Ти), из которой следует быстрое уменьшение h или повышение степени однородности реакционной среды по мере увеличения Ти . При Ти » 540 К показатель h=0, т.е., реакционная среда становится однородной (гомогенной).
связаны между собой уравнением (3.18). На рис. 5.3 приведена зависимость h(Ти), из которой следует быстрое уменьшение h или повышение степени однородности реакционной среды по мере увеличения Ти . При Ти » 540 К показатель h=0, т.е., реакционная среда становится однородной (гомогенной).
Авторы [2] показали, что температура плавления Тпл для исследуемых полиимидов примерно равна 800К. Исходя из известного правила двух третей [11]:
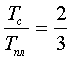 , (5.3)
, (5.3)
температуру стеклования Тс полиимида можно оценить как равную ~533К. Иначе говоря, как и следовало ожидать [12,13], реакционная среда в случае твердофазной имидизации становится однородной (евклидовой) при переходе стеклования.
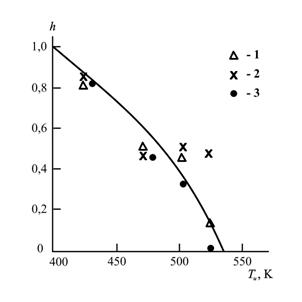
Рис.5.3. Зависимость показателя неоднородности h реакционной системы от температуры, имидизации Ти для твердофазной имидизации при содержании Na+-монтмориллонита Wс: 0(1), 2(2) и 5(3) вес.% [8].
Форма кривой h(Ти), показанная на рис. 5.3, т.е., стремление h→0 при повышении температуры, предполагает, что фракталоподобные эффекты, а именно, вариация ![]() , связаны с энергетическим беспорядком [10].
, связаны с энергетическим беспорядком [10].
Рассмотрим физические основы изменения степени связности реакционной системы, характеризуемой эффективной спектральной размерностью ![]() , по мере изменения температуры имидизации Ти и содержанияNa+-монтмориллонита Wс. Как и ранее, величину фрактальной размерности макромолекулярного клубка Dfможно оценить с помощью формулы (2.9). На рис. 5.4 приведена зависимость
, по мере изменения температуры имидизации Ти и содержанияNa+-монтмориллонита Wс. Как и ранее, величину фрактальной размерности макромолекулярного клубка Dfможно оценить с помощью формулы (2.9). На рис. 5.4 приведена зависимость ![]() от Df, из которой следует увеличение
от Df, из которой следует увеличение ![]() по мере снижения Df и приDf→1,50 (протекаемый клубок [5]), величина
по мере снижения Df и приDf→1,50 (протекаемый клубок [5]), величина![]() быстро стремится к своей предельной величине
быстро стремится к своей предельной величине ![]() =2,0 [10]. Такая форма зависимости
=2,0 [10]. Такая форма зависимости ![]() ( Df) позволяет делать два вывода. Во-первых, существует определенная взаимосвязь
( Df) позволяет делать два вывода. Во-первых, существует определенная взаимосвязь ![]() и Df, характеризуемая кривой рис 5.4. Во-вторых, величину
и Df, характеризуемая кривой рис 5.4. Во-вторых, величину ![]() нельзя рассматривать как спектральную размерность собственно макромолекулярного клубка, поскольку в этом случае теория предполагает уменьшение
нельзя рассматривать как спектральную размерность собственно макромолекулярного клубка, поскольку в этом случае теория предполагает уменьшение ![]() по мере снижения Df [14]:
по мере снижения Df [14]:
![]() , (5.4)
, (5.4)
где d-размерность евклидова пространства, в котором рассматривается фрактал (очевидно в нашем случае d=3).
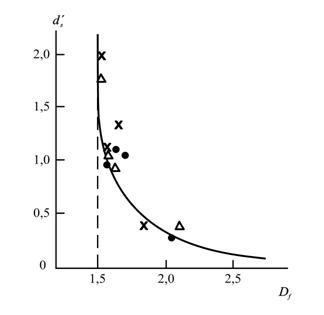
Рис. 5.4. Зависимость эффективной спектральной размерности ![]() реакционной среды от фрактальной размерности макромолекулярного клубка Df в процессе имидизации. Обозначения те же, что и на рис . 5.3 [8].
реакционной среды от фрактальной размерности макромолекулярного клубка Df в процессе имидизации. Обозначения те же, что и на рис . 5.3 [8].
Исходя из сказанного выше, следует предположить, что в рассматриваемом случае ![]() является показателем связанности реакционной среды, каким-то образом, связанным со структурой макромолекулярного клубка, характеризуемой размерностью Df. Рассмотрим одну из возможных теоретических схем такой взаимосвязи.
является показателем связанности реакционной среды, каким-то образом, связанным со структурой макромолекулярного клубка, характеризуемой размерностью Df. Рассмотрим одну из возможных теоретических схем такой взаимосвязи.
Хорошо известно [15], что в химических реакциях большое значение имеет стерический фактор ρ(ρ≤1), показывающий, что не все соударения реагентов происходят с надлежащей для образования продукта реакции ориентацией реагирующих молекул. Величина ρ определяется размерностью Df и может быть рассчитана согласно уравнению (2.41). Как следует из этого уравнения, величина ρ увеличивается по мере снижения Df. Число мест Nакт макромолекулярного клубка, способных принимать участие в химической реакции (активных мест) определяется так [16]:
![]() . (5.5)
. (5.5)
Обратим внимание, что ![]() в соотношении (5.2). Но в случае химической реакции не все активные места макромолекулярного клубка могут реагировать в силу условия ρ<1, а только их часть Nρ, пропорциональная ρ. Для предварительных оценок можно предположить:
в соотношении (5.2). Но в случае химической реакции не все активные места макромолекулярного клубка могут реагировать в силу условия ρ<1, а только их часть Nρ, пропорциональная ρ. Для предварительных оценок можно предположить:
Np=100ρ. (5.6)
Полагая для реакции имидизации без наполнителя при Ти=423К Df=2,12, ![]() =0,42, т.е., экспериментально определенные величины, можно рассчитать значение ρ согласно уравнению (2.41), затем величину Nρ согласно уравнению (5.5) и определить постоянный коэффициент в соотношении (5.5) при t=const=15мин., который равен 2. Далее, используя этот коэффициент в уравнении (5.5), можно рассчитать величины
=0,42, т.е., экспериментально определенные величины, можно рассчитать значение ρ согласно уравнению (2.41), затем величину Nρ согласно уравнению (5.5) и определить постоянный коэффициент в соотношении (5.5) при t=const=15мин., который равен 2. Далее, используя этот коэффициент в уравнении (5.5), можно рассчитать величины ![]() , которые в дальнейшем будут обозначены как (
, которые в дальнейшем будут обозначены как (![]() )Т, для реакции имидизации с варьируемыми Ти и Wс. На рис. 5.5 приведено сравнение величин
)Т, для реакции имидизации с варьируемыми Ти и Wс. На рис. 5.5 приведено сравнение величин ![]() , определенных из наклонов графиков ρА(t) в двойных логарифмических координатах (см. рис. 5.1 и 5.2), и (
, определенных из наклонов графиков ρА(t) в двойных логарифмических координатах (см. рис. 5.1 и 5.2), и (![]() )Т, рассчитанных согласно уравнениям (2.41), (5.5) и (5.6). Как можно видеть, между этими параметрами получено хорошее соответствие. Это означает, что связность реакционного пространства, характеризуется размерностью
)Т, рассчитанных согласно уравнениям (2.41), (5.5) и (5.6). Как можно видеть, между этими параметрами получено хорошее соответствие. Это означает, что связность реакционного пространства, характеризуется размерностью ![]() , зависит от размерности макромолекулярного клубка, причем эта зависимость является специфической именно для химических реакций благодаря введению стерического фактора ρ [9].
, зависит от размерности макромолекулярного клубка, причем эта зависимость является специфической именно для химических реакций благодаря введению стерического фактора ρ [9].
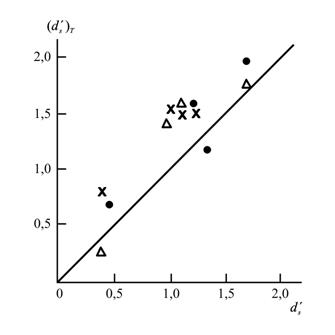
Рис.5.5. Сравнение рассчитанных согласно соотношению (5.2) ![]() и уравнениям (2.41), (5.5) и (5.6) (
и уравнениям (2.41), (5.5) и (5.6) (![]() )Твеличин эффективной спектральной размерности реакционной среды в процессе имидизации. Обозначения те же, что и на рис. 5.3 [8].
)Твеличин эффективной спектральной размерности реакционной среды в процессе имидизации. Обозначения те же, что и на рис. 5.3 [8].
С точки зрения химии процесса это можно трактовать следующим образом: чем меньше Df, тем более открыта структура макромолекулярного клубка, тем легче протекает процесс дегидратации (удаления воды) и замыкание имидного кольца [2].
Следовательно, рассмотренные выше данные продемонстрировали, что основным параметром, контролирующем скорость однофазной имидизации, является степень связности реакционной системы, характеризуемая ее эффективной спектральной размерностью. В свою очередь эта размерность является функцией структуры макромолекулярного клубка, что составляет специфику полимерных реакций. Увеличение температуры имидизации определяет снижение неоднородности реакционной среды и соответствующее увеличение степени ее связности [4,18].
В работе [17] количественный анализ температурной зависимости кинетики имидизации был дан в рамках еще одной концепции, а именно, фрактальной модели кинетики химических реакций [4,18]. Авторы предположили, что причиной ускорения реакции имидизации по мере роста ее температуры Ти является изменение структуры макромолекулярного клубка полиимида, которое является следствием изменения его молекулярных характеристик. В качестве последней в работе [17] было выбрано характеристическое отношение С∞, которое является показателем статической гибкости полимерной цепи [19]. Как и ранее, структуру макромолекулярного клубка характеризовали ее фрактальной (хаусдорфовой) размерностью Df. Взаимосвязь С∞ и Df дается уравнением [20]:
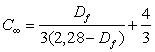 . (5.7)
. (5.7)
Температурную зависимость С∞ (и, следовательно, Df) можно рассчитать, используя уравнение, предложенное в работе [13]:
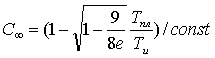 , (5.8)
, (5.8)
где Тпл- температура плавления, равная для исследуемых нанокомпозитов ~800К [2].
Для определения константы в уравнении (5.8) используем следующий метод. Общее уравнение фрактальной кинетики химических реакций имеет вид формулы (3.10). Построением зависимости Q(t) в двойных логарифмических координатах при Ти =523К была определена величина Df=1,59, затем из уравнения (5.7) соответствующее ей значение С∞ и из уравнения (5.8) – величина оцениваемой константы. Далее для остальных температур имидизации были рассчитаны величины С∞ (общая вариация 3,51÷4,52) и соответствующие им значения Df (общая вариация 1,59÷1,81). Затем по уравнению (3.10) рассчитывались кинетические кривые Q(t). Величина исходной вязкости реакционной среды η0 в этом случае принималась постоянной и равной 1 (с учетом того факта, что реакция протекает в твердой фазе), а величина с0 определена методом подбора при условии наилучшего соответствия теоретических и экспериментальных кривых Q(t). На рис. 5.6 точками показано выполненное рассмотренным способом моделирование кинетических кривых твердофазной имидизации. Как можно видеть, получено хорошее соответствие теории и эксперимента.
Подбор исходной концентрации реагентов (или активных центров реакции) с0 показал ее увеличение в интервале 6,5÷35 относительных единиц по мере роста температуры имидизации Ти в интервале 423÷523К. Объяснить это увеличение с0 также можно в рамках фрактальной концепции кинетики химических реакций, согласно которой [4]:
ММ ~ С0tобщ, (5.9)
где М – молекулярная масса продукта реакции, tобщ-продолжительность реакции.
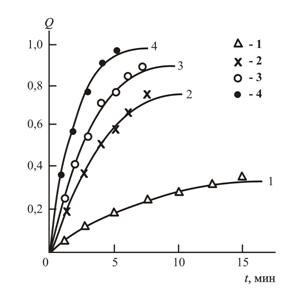
Рис.5.6. Кинетические Q(t) твердофазной имидизации при температурах: 423 (1,5), 473 (2,6), 503 (3,7) и 523К (4,8). 1÷4-экспериментальные данные; 5÷8-расчет по уравнению (3.10) [17].
Полагая ММ=const, получим теоретическое значение С0(С0Т) из соотношения (5.9) [17]
C0T ~ tобщ-1 (5.10)
Принимая в качестве tобщ продолжительность участка реакции имидизации, на котором выполняются закономерности реакции первого порядка и на котором в основном завершается имидизация, можно оценить
величины ![]() , которые сравниваются с полученными методом подбора значениями С0 на рис. 5.7. Как следует из данных этого рисунка, между значениями
, которые сравниваются с полученными методом подбора значениями С0 на рис. 5.7. Как следует из данных этого рисунка, между значениями ![]() и С0 наблюдается линейная корреляция, проходящая через начало координат. Такое соответствие предполагает, что величина С0 (число активных центров имидизации) возрастает по мере увеличения Ти за счет интенсификации диффузионных процессов [4].
и С0 наблюдается линейная корреляция, проходящая через начало координат. Такое соответствие предполагает, что величина С0 (число активных центров имидизации) возрастает по мере увеличения Ти за счет интенсификации диффузионных процессов [4].
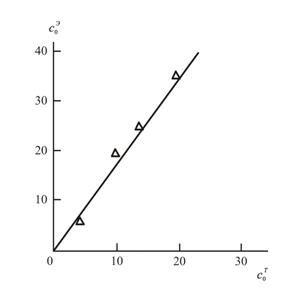
Рис.5.7. Соотношение полученных подбором С0 и рассчитанных согласно соотношению (5.10) ![]() числа активных центров реакции имидизации [17].
числа активных центров реакции имидизации [17].
Следовательно, изложенные выше факты показали, что фрактальная кинетика химических реакций количественно описывает кинетику процесса твердофазной имидизации при разных температурах. Это описание дано в рамках только физических аспектов реакции и не затрагивает ее химической стороны. Рост эффективной исходной концентрации реагентов со по мере роста температуры имидизации обусловлен также физической причиной - усилением диффузией реагентов в твердофазном состоянии.
Следует указать, что введение наполнителя в реакционную смесь приводит к образованию двухфазной системы, где важную (или решающую) роль будут играть межфазные взаимодействия [21]. В частности, взаимодействие ПАК-Na+ - монтмориллонит должно привести к изменению структуры формирующегося макромолекулярного клубка полиимида (ПИ) [22] и аналогичный эффект дает повышение температуры имидизации Ти [23]. Поэтому авторы работы [24] выполнили структурный анализ процессов, протекающих в ходе реакции твердофазной имидизации, с учетом указанного выше аспекта.
Рассмотрим вопрос межфазных взаимодействий формирующегося макромолекулярного клубка ПИ и Na+ -монтмориллонита на поверхности наполнителя. Как показал Пфейфер [22], макромолекулярный клубок на твердой поверхности изменяет свою конфигурацию (структуру), которую можно охарактеризовать ее фрактальной размерностью Df . Это изменение описывается с помощью следующего уравнения [22]:
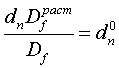 , (5.11)
, (5.11)
где dn и dn0 – фрактальные размерности поверхности нанонаполнителя в нанокомпозите и в исходном состоянии, ![]() и Df – фрактальные размерности макромолекулярного клубка ПИ в растворе (смешивание ПАК и Na+ - монтмориллонита производилось в растворе диметилацетамида [2]) и в твердофазном состоянии на поверхности нанонаполнителя, соответственно.
и Df – фрактальные размерности макромолекулярного клубка ПИ в растворе (смешивание ПАК и Na+ - монтмориллонита производилось в растворе диметилацетамида [2]) и в твердофазном состоянии на поверхности нанонаполнителя, соответственно.
Рассмотрим оценку параметров, входящих в уравнение (5.11). Как показано в работе [25], полимерная цепь, обладающая конечной жесткостью и состоящая из статических сегментов конечной длины, в состоянии воспроизводить растущую шероховатость поверхности по мере увеличения ![]() и при
и при![]() >2,5 величина dn определяется так:
>2,5 величина dn определяется так:
dn=5-![]() . (5.12)
. (5.12)
Для Na+ - монтмориллонита величина ![]() определена экспериментально и равна 2,78 [27]. Величину
определена экспериментально и равна 2,78 [27]. Величину ![]() в первом приближении можно принять равной размерности макромолекулярного клубка в хорошем растворителе (
в первом приближении можно принять равной размерности макромолекулярного клубка в хорошем растворителе (![]() =1,667 [5]). Тогда оценка по уравнению (5.11) дает
=1,667 [5]). Тогда оценка по уравнению (5.11) дает![]() =1,33. Очевидно, что эта размерность макромолекулярного клубка, вытянутого на поверхности Na+ - монтмориллонита и в дальнейшем она будет обозначена как
=1,33. Очевидно, что эта размерность макромолекулярного клубка, вытянутого на поверхности Na+ - монтмориллонита и в дальнейшем она будет обозначена как ![]() .
.
Расчет действительных значений фрактальной размерности ![]() макромолекулярного клубка для реакции первого порядка, которой является твердофазная имидизация [2], можно выполнить с помощью уравнения (2.9). Расчет по этому уравнению показал, что для исследуемых реакций имидизации
макромолекулярного клубка для реакции первого порядка, которой является твердофазная имидизация [2], можно выполнить с помощью уравнения (2.9). Расчет по этому уравнению показал, что для исследуемых реакций имидизации ![]() =1,59÷2,12. Иначе говоря, для всех случаев реальной реакции имидизации выполняется условие:
=1,59÷2,12. Иначе говоря, для всех случаев реальной реакции имидизации выполняется условие: ![]() <
<![]() . Такое соотношение позволяет предположить, что только часть макромолекулярных клубков ПИ взаимодействуют с поверхностью Na+-монтмориллонита. Это подтверждается данными рис. 5.8, где разность Δ
. Такое соотношение позволяет предположить, что только часть макромолекулярных клубков ПИ взаимодействуют с поверхностью Na+-монтмориллонита. Это подтверждается данными рис. 5.8, где разность Δ![]() =
=![]() -
-![]() нанесена на график как функция содержания нанонаполнителя Wс для четырех температур имидизации. Как следует из графика этого рисунка, величина Δ
нанесена на график как функция содержания нанонаполнителя Wс для четырех температур имидизации. Как следует из графика этого рисунка, величина Δ![]() уменьшается по мере роста Wс или
уменьшается по мере роста Wс или ![]() →
→![]() и экстрополяция этих графиков показывает, что приWс≈17,5 вес.%
и экстрополяция этих графиков показывает, что приWс≈17,5 вес.% ![]() =
=![]() или Δ
или Δ![]() =0. Отметим, что указанная величина Wс справедлива только для эсфолиированного (неагрегированного) нанонаполнителя.
=0. Отметим, что указанная величина Wс справедлива только для эсфолиированного (неагрегированного) нанонаполнителя.
Уменьшение Δ![]() по мере роста Wс предполагает повышение доли взаимодействующей фазы φвз в процессе имидизации. Величину φвз можно определить согласно правилу смесей из уравнения [24]:
по мере роста Wс предполагает повышение доли взаимодействующей фазы φвз в процессе имидизации. Величину φвз можно определить согласно правилу смесей из уравнения [24]:
![]() , (5.13)
, (5.13)
где ![]() - фрактальная размерность макромолекулярного клубка в отсутствие нанонаполнителя.
- фрактальная размерность макромолекулярного клубка в отсутствие нанонаполнителя.
На рис. 5.9 приведена зависимость ![]() для Ти=423К. Как можно видеть, эта корреляция линейна, проходит через начало координат и аналитически описывается следующим эмпирическим уравнением [24]:
для Ти=423К. Как можно видеть, эта корреляция линейна, проходит через начало координат и аналитически описывается следующим эмпирическим уравнением [24]:
φвз=0,0575Wс, (5.14)
где Wс-дано в вес. %.
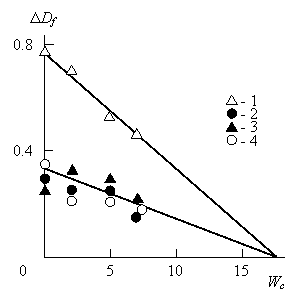
Рис. 5.8. Зависимости разности фрактальной размерности
Δ![]() =
=![]() -
-![]() от содержания нанонаполнителя Wс для нанокомпозитов полиимид/Na+-монтмориллонит при температурах имидизации: 423 (1), 473 (2), 503 (3) и 523 (4) [24].
от содержания нанонаполнителя Wс для нанокомпозитов полиимид/Na+-монтмориллонит при температурах имидизации: 423 (1), 473 (2), 503 (3) и 523 (4) [24].

Рис.5.9.Зависимость относительной доли взаимодействующей фазы φвз от содержания наполнителя Wс для нанокомпозитов полиимид/Na+ -монтмориллонит при температурах имидизации: 423К [24].
Очевидно, что при Wс=17,5 вес.%, полученной экстраполяцией графиков рис. 5.8, величина φвз≈1,0, т.е., в реакции имидизации задействована вся реакционная система ПАК-Na+- монтмориллонит, тогда как при Wс<17,5 вес.% имидизация частично протекает в твердофазной ПАК без воздействия Na+- монтмориллонита.
На рис 5.10 приведена зависимость константы скорости реакции k1 от относительной доли взаимодействующей фазы φвз, которая оказалась приблизительно линейной и показала рост k1 по мере увеличения φвз. Это позволяет предположить прямую зависимость скорости твердофазной имидизации от уровня межфазных взаимодействий в реакционной системе [24].

Рис.5.10. Зависимость константы скорости реакции первого порядка k1 от относительной доли взаимодействующей фазы φвз для нанокомпозитов полиимид/Na+ -монтмориллонит при температурах имидизации 423 К [24].
В работе [2] было обнаружено снижение энергии активации процесса имидизации Еакт по мере увеличенияWс-от 66 до 55 кДж/моль в интервале Wс=0÷7 вес.%. Ранее авторы [28] предложили следующую зависимость Еактот Df в случае термоокислительной деструкции полиарилата:
![]() . (5.15)
. (5.15)
В табл. 5.1 приведено сравнение экспериментальных Еакт и рассчитанных согласно уравнению (5.15) ![]() величин энергии активации для твердофазной имидизации. Как можно видеть между указанными значениями энергии активации получено хорошее соответствие (среднее расхождение
величин энергии активации для твердофазной имидизации. Как можно видеть между указанными значениями энергии активации получено хорошее соответствие (среднее расхождение![]() и
и ![]() составляет менее 5%). Это означает, что энергии ассоциации (реакция имидизации) и диссоциации (термоокислительная деструкция) примерно равны, что и следовало ожидать.
составляет менее 5%). Это означает, что энергии ассоциации (реакция имидизации) и диссоциации (термоокислительная деструкция) примерно равны, что и следовало ожидать.
Следовательно, полученные выше результаты вновь продемонстрировали, что причиной ускорения процесса имидизации по мере роста содержания нанонаполнителя является изменение структуры макромолекулярного клубка вследствие межфазных взаимодействий с поверхностью Na+-монтмориллонита. Относительная доля взаимодействующей фазы растет по мере увеличения содержания нанонаполнителя и при его содержании примерно17,5 вес.% эта фаза занимает всю реакционную систему. Снижение энергии активации процесса имидизации по мере роста содержания нанонаполнителя также обусловлено структурными факторами, а именно снижением фрактальной размерности макромолекулярного клубка.
Авторы [2] обнаружили, что кинетические кривые Q(t) имеют типичную для реакций полимеризации форму с автозамедлением, показывающую снижение скорости имидизации со временем (см. рис. 5.6). Как известно [10], такие кривые Q(t) характерны для протекания реакции в неоднородной среде и описываются простым соотношением (2.15). Указанное соотношение предполагает сильное влияние степени этой неоднородности, характеризуемой показателем h, на скорость реакции. Поэтому в работах [28,29] предпринята попытка выяснения физического смысла неоднородности реакционной среды в случае твердофазной имидизации ПАК и факторов, определяющих величину показателя неоднородности (гетерогенности) среды.
Таблица 5.1.
Сравнение экспериментальных Еакт и рассчитанных согласно уравнению (5.15) ![]() величины энергии активации процесса твердофазной имидизации[24]
величины энергии активации процесса твердофазной имидизации[24]
| Wс, вес.% | кДж/моль | кДж/моль |
| 0 | 66,0 | 68,6 |
| 2 | 57,5 | 63,4 |
| 5 | 54,0 | 52,8 |
| 7 | 51,5 | 49,3 |
Реакцию твердофазной имидизации в наиболее простом и общем виде можно представить соотношением (5.1), которое может быть описано скейлинговым соотношением (5.2) для диффузионно-ограниченных реакций. На рис. 5.1 приведены зависимости ρа(t) в двойных логарифмических координатах, соответствующие соотношению (5.2), для реакции твердофазной имидизации без нанонаполнителя при четырех температурах имидизации Ти. Как отмечалось выше, полученные зависимости линейны и по их наклону можно определить величину спектральной размерности ds, характеризующей связность реакционной среды, в соотношении (5.2). Повышение Ти в интервале 423÷523К приводит к существенному росту ds: от 0,42 до 1,68. Отметим, что такое увеличение ds происходит без изменения состава реакционной смеси. Это означает, что энергетические ограничения приводят к появлению фрактального пространства, в котором вместо величины ds должна быть использована эффективная спектральная размерность ![]() , отражающая наличие указанных выше ограничений и связанная с ds уравнением [10]:
, отражающая наличие указанных выше ограничений и связанная с ds уравнением [10]:
![]() , (5.16)
, (5.16)
где βn-параметр характеризующий распределение времен «скачков» (перемещений) реагента.
На рис. 5.3 приведена зависимость h(Ти), из которой следует быстрое уменьшение h или повышение однородности реакционной среды по мере увеличения Ти. При Ти≈540К показатель h=0, т.е., реакционная среда становится однородной (гомогенной). Поскольку для ПИ Тс≈533К, то, как и следовало ожидать [12], реакционная среда в случае твердофазной имидизации становится однородной (евклидовой) при переходе стеклования.
Форма кривой h(Ти), показанная на рис. 5.3, т.е., стремление h→0 при повышении температуры, предполагает, что фракталоподобные эффекты, а именно, вариация ![]() , связаны с энергетическим беспорядком [10]. В таком случае энергетическое состояние структуры полимера может быть охарактеризовано размерностью областей локализации избыточной энергии
, связаны с энергетическим беспорядком [10]. В таком случае энергетическое состояние структуры полимера может быть охарактеризовано размерностью областей локализации избыточной энергии ![]() [30]. Величину
[30]. Величину ![]() можно оценить из следующего уравнения [31]:
можно оценить из следующего уравнения [31]:
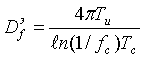 , (5.17)
, (5.17)
где fc - относительный свободный флуктуационный объем, определяемый с помощью уравнений (1.23), (1.28) и (1.29).
На рис. 5.11 приведена зависимость h(Dfэ), из которой следует ожидаемый результат: повышение степени энергетической возбужденности структуры нанокомпозита, обусловленное «закачкой» тепловой энергии по мере роста Ти характеризуемая размерностью Dfэ, приводит к снижению h. При Dfэ ≈ 6,3 реакционная среда становится однородной (h=0).
Таким образом, данные рис. 5.3 и 5.11 дают ответ на вопрос, при каких условиях h=0, т.е., когда реакционная среда становится однородной. Тем не менее, физика этого процесса остается неясной. Переход стеклования не дает сингулярности ни в поведении флуктуационного свободного объема fс, ни в поведении ![]() . Поэтому для объяснения перехода неоднородная
. Поэтому для объяснения перехода неоднородная ![]() однородная среда использованы представления концепции фрактального (локального) свободного объема
однородная среда использованы представления концепции фрактального (локального) свободного объема ![]() (подробнее см. раздел 1.2). Согласно этой концепции микрополость свободного объема следует моделировать не трехмерной сферой с объемом νh, как это принято в классической физике полимеров [32], а
(подробнее см. раздел 1.2). Согласно этой концепции микрополость свободного объема следует моделировать не трехмерной сферой с объемом νh, как это принято в классической физике полимеров [32], а ![]() -мерной сферой с объемом
-мерной сферой с объемом ![]() . В этом случае между fс и
. В этом случае между fс и ![]() получено соотношение (1.10). Величина νh может быть рассчитана следующим образом [31]:
получено соотношение (1.10). Величина νh может быть рассчитана следующим образом [31]:
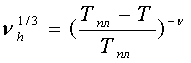 , (5.18)
, (5.18)
где перколяционный индекс ν принят равным 0,85 [33].
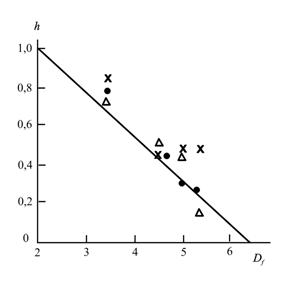
Рис.5.11. Зависимость показателя неоднородности h от размерности областей локализации избыточной энергии ![]() , для твердофазной имидизации ПАК при содержании Na+ -монтмориллонита Wс: 0 (1), 2 (2) и 5 (3) вес.% [29].
, для твердофазной имидизации ПАК при содержании Na+ -монтмориллонита Wс: 0 (1), 2 (2) и 5 (3) вес.% [29].
Далее из геометрических соображений в предположении трехмерной микрополости свободного объема можно оценить ее радиус rh, а затем рассчитать ![]() согласно уравнению (1.9).
согласно уравнению (1.9).
На рис. 5.12 приведена зависимость h(![]() ),где величина
),где величина ![]() рассчитана согласно уравнениям (1.9), (1.10) и (5.18). Как следует из данных этого рисунка, величина h = 0 или однородность реакционной среды достигается при
рассчитана согласно уравнениям (1.9), (1.10) и (5.18). Как следует из данных этого рисунка, величина h = 0 или однородность реакционной среды достигается при ![]() =0,34. Напомним, что указанная величина
=0,34. Напомним, что указанная величина ![]() соответствует порогу перколяции для схемы перекрывающихся сфер [34]. Иначе говоря, при
соответствует порогу перколяции для схемы перекрывающихся сфер [34]. Иначе говоря, при ![]() =0,34 микрополости флуктуационного свободного объема моделируемые
=0,34 микрополости флуктуационного свободного объема моделируемые ![]() -мерной сферой, образуют непрерывный перколяционный каркас или непрерывные каналы диффузии [35]. Таким образом, между однородной и неоднородной средой, по крайней мере, в случае твердофазной имидизации, существует качественное различие. Для неоднородной реакционной среды продукт дегидратации (молекула воды), находящаяся в микрополости свободного объема, вынуждена «ждать» открытия перекрывающей ее соседней микрополости, после чего она совершит «скачок» из первой во вторую и далее процесс повторяется. Для однородной реакционной среды такой процесс «ожидания» не требуется в силу наличия сквозных перколяционных каналов свободного объема. Отметим, что указанные процессы «скачков» реализуются на локальном уровне. Указанный эффект является причиной интенсификации диффузных процессов в ходе твердофазной имидизации, о которой упоминалось выше.
-мерной сферой, образуют непрерывный перколяционный каркас или непрерывные каналы диффузии [35]. Таким образом, между однородной и неоднородной средой, по крайней мере, в случае твердофазной имидизации, существует качественное различие. Для неоднородной реакционной среды продукт дегидратации (молекула воды), находящаяся в микрополости свободного объема, вынуждена «ждать» открытия перекрывающей ее соседней микрополости, после чего она совершит «скачок» из первой во вторую и далее процесс повторяется. Для однородной реакционной среды такой процесс «ожидания» не требуется в силу наличия сквозных перколяционных каналов свободного объема. Отметим, что указанные процессы «скачков» реализуются на локальном уровне. Указанный эффект является причиной интенсификации диффузных процессов в ходе твердофазной имидизации, о которой упоминалось выше.
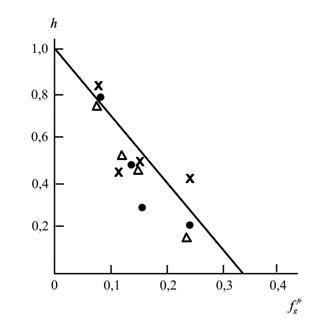
Рис.5.12. Зависимость показателя неоднородности h реакционной среды от относительного фракталь-ного свободного объема ![]() для твердофазной имидизации ПАК. Обозначения те же, что и на рис. 5.11 [29].
для твердофазной имидизации ПАК. Обозначения те же, что и на рис. 5.11 [29].
И, наконец, на рис. 5.13 приведена зависимость коэффициента βn в уравнении (5.16) от ![]() . Снова величина βn достигает своего предельного значения βn=1 (т.е.,
. Снова величина βn достигает своего предельного значения βn=1 (т.е., ![]() =
=![]() ) при
) при ![]() =0,34. Соотношение βn и
=0,34. Соотношение βn и ![]() дается простым эмпирическим уравнением [29]:
дается простым эмпирическим уравнением [29]:
βn =2,94![]() . (5.19)
. (5.19)
График рис. 5.13 демонстрирует, что энергетическим ограничением, определяющим переход от ![]() к
к ![]() , является необходимость «скачков» продуктов реакции или реагентов между микрополостями свободного объема. Понятно, что увеличение Ти снижает время ожидания «скачка», а образование сквозных перколяционных каналов микрополостей свободного объема снимает эти ограничения.
, является необходимость «скачков» продуктов реакции или реагентов между микрополостями свободного объема. Понятно, что увеличение Ти снижает время ожидания «скачка», а образование сквозных перколяционных каналов микрополостей свободного объема снимает эти ограничения.
Следовательно, рассмотренные выше результаты продемонстрировали, что понятие неоднородности реакционной среды в случае твердофазной имидизации связано с представлениями свободного объема, что следовало ожидать для диффузионно-контролируемых реакций в твердофазном состоянии полимеров. Если микрополости свободного объема не связаны друг с другом, то среда является неоднородной, а в случае образования перколяционного каркаса таких микрополостей - однородной. Получить такое определение можно только в рамках концепции фрактальногосвободного объема.
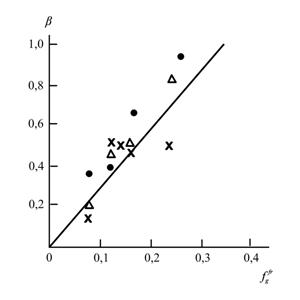
Рис.5.13. Зависимость коэффициента βn в уравнении (5.16) от относительного фрактального свободного объема ![]() для твердофазной имидизации ПАК. Обозначения те же, что и на рис. 5.11 [29].
для твердофазной имидизации ПАК. Обозначения те же, что и на рис. 5.11 [29].
Как показано в работе [2], увеличение температуры имидизации Ти в интервале 423÷523К и содержания наполнителя Wс в интервале 0÷7 вес.% приводит к существенным изменениям кинетики имидизации, выраженных двумя основными аспектами: существенным увеличением скорости реакции (константа скорости реакции первого порядка k1 увеличивается почти на два порядка) и ростом предельной степени конверсии (имидизации) Qпр от примерно 0,25 для реакции имидизации без наполнителя при Ти=423К до 1,0 при содержании Na+- монтмориллонита 7вес.% и Ти=523К. Напомним также, что все кинетические кривые Q(t) для указанных реакции имидизации имеют типичную форму кривых с автозамедлением (см. рис. 5.6), характерную для фрактальных реакций, т.е., либо реакций фрактальных объектов, либо реакций во фрактальных пространствах [36]. Иначе говоря, указанные аспекты реакции имидизации в достаточной степени имеют общий характер. Если для первого эффекта (увеличения k1) авторы [2] предложили вероятную химическую трактовку, рассматривая нанонаполнитель как катализатор, то второй эффект (повышение Qпр) объяснения не получил, хотя его теоретическая и практическая важность очевидны. Поэтому ниже будет предложена структурная трактовка предельной степени конверсии в процессе твердофазной имидизации, основанная на общих принципах фрактального анализа [36].
Как известно [5,6], макромолекулярный клубок в различных состояниях полимера (раствор, расплав, твердая фаза) представляет собой фрактальный объект, характеризуемой фрактальной (хаусдорфовой) размерностью ![]() . Специфической особенностью фрактальных объектов является распределение их массы в пространстве: плотность ρ такого объекта изменяется при вариации его радиуса R следующим образом. [38]:
. Специфической особенностью фрактальных объектов является распределение их массы в пространстве: плотность ρ такого объекта изменяется при вариации его радиуса R следующим образом. [38]:
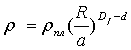 , (5.20)
, (5.20)
где ρпл- плотность материала, из которого состоит фрактальный объект в состоянии плотной упаковки, а-нижний линейный масштаб фрактального поведения объекта, d-размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d=3).
Из уравнения (5.20) следует уменьшение ρ по мере снижения ![]() , поскольку всегда
, поскольку всегда ![]() <d, что, естественно, облегчает доступ реагентов во внутренние области макромолекулярного клубка и приводит к более полным химическим превращениям, т.е., к увеличению степени конверсии Qпр. Кроме того, известно [38], что при формировании макромолекулярного клубка механизмами необратимой агрегации в его центральной области образуется плотноупакованный домен, где протекание химических реакций невозможно. Исходя из этого, можно утверждать, что для химической реакции доступа только часть макромолекулярного клубка, которая тем больше, чем меньше его фрактальная размерность
<d, что, естественно, облегчает доступ реагентов во внутренние области макромолекулярного клубка и приводит к более полным химическим превращениям, т.е., к увеличению степени конверсии Qпр. Кроме того, известно [38], что при формировании макромолекулярного клубка механизмами необратимой агрегации в его центральной области образуется плотноупакованный домен, где протекание химических реакций невозможно. Исходя из этого, можно утверждать, что для химической реакции доступа только часть макромолекулярного клубка, которая тем больше, чем меньше его фрактальная размерность ![]() . В случае протекаемого клубка (
. В случае протекаемого клубка (![]() ≤1,5 [5]) через него могут свободно проходить как низко-, так и высокомолекулярные вещества и это предполагает, что в таком случае величина Qпр=1,0. При
≤1,5 [5]) через него могут свободно проходить как низко-, так и высокомолекулярные вещества и это предполагает, что в таком случае величина Qпр=1,0. При ![]() =2,5 химическая реакция прекращается и начинается процесс гелеобразования [39,40]. Это означает, что при достижении
=2,5 химическая реакция прекращается и начинается процесс гелеобразования [39,40]. Это означает, что при достижении ![]() =2,5 Qпр=0. Указанные оценки позволяют записать дробный показатель νдр для реакций синтеза полимеров аналогично определению, принятому в работе [41]:
=2,5 Qпр=0. Указанные оценки позволяют записать дробный показатель νдр для реакций синтеза полимеров аналогично определению, принятому в работе [41]:
![]() , (5.21)
, (5.21)
где ![]() -величина
-величина ![]() при гелеобразовании, равная 2,5.
при гелеобразовании, равная 2,5.
Напомним, что согласно [42] величина νдр характеризует долю состояний системы, не изменяющихся в процессе ее эволюции. В случае химических реакций вообще и процесса имидизации в частности это предполагает, что величина νдр характеризует часть макромолекулярного клубка, недоступную для химических превращений. Тогда доступная для таких превращений часть клубка βd определяется следующим образом [41]:
βd = 1- νдр = 2,5-![]() . (5.22)
. (5.22)
Исходя из сказанного выше, можно определить предельную степень конверсии следующим тождеством [43]:
Qпр= βd. (5.23)
Таким образом, проблема оценки Qпр сводится к вопросу определения фрактальной размерности ![]() . Как отмечалось выше, в настоящее время существует два метода определения указанной размерности. Первый метод заключается в использовании общего соотношения фрактальной кинетики химических реакций-уравнения (3.10). Кроме того, расчет размерности
. Как отмечалось выше, в настоящее время существует два метода определения указанной размерности. Первый метод заключается в использовании общего соотношения фрактальной кинетики химических реакций-уравнения (3.10). Кроме того, расчет размерности ![]() позволяет уравнение (2.9).
позволяет уравнение (2.9).
Построение зависимостей Q(t) в двойных логарифмических координатах позволяет определить величину ![]() по наклону этих зависимостей в случае их линейности согласно уравнению (3.10). На рис. 5.14 приведены указанные зависимости для процесса имидизации ПАК без наполнителя. Как можно видеть, эти зависимости линейны, что позволяет выполнить оценку
по наклону этих зависимостей в случае их линейности согласно уравнению (3.10). На рис. 5.14 приведены указанные зависимости для процесса имидизации ПАК без наполнителя. Как можно видеть, эти зависимости линейны, что позволяет выполнить оценку ![]() указанным методом.
указанным методом.
На рис. 5.15 приведено сравнение размерностей ![]() , рассчитанных двумя методами (
, рассчитанных двумя методами (![]() и
и ![]() соответственно). Как следует из приведенного графика, оба эти метода дают близкие величины
соответственно). Как следует из приведенного графика, оба эти метода дают близкие величины ![]() и поэтому в дальнейшем будет использована их средняя величина, т.е.,
и поэтому в дальнейшем будет использована их средняя величина, т.е., ![]() = (
= (![]() +
+ ![]() )/2.
)/2.
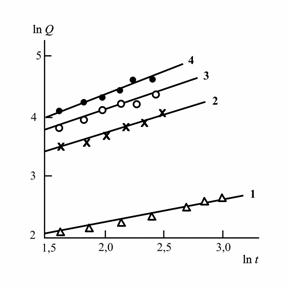
Рис.5.14. Зависимость степени имидизации Q от продолжитель-ности реакции t в двойных логарифмических координатах для процесса имидизации ПАК при температуре: 423 (1), 473 (2), 503 (3) и 523К (4) [37].
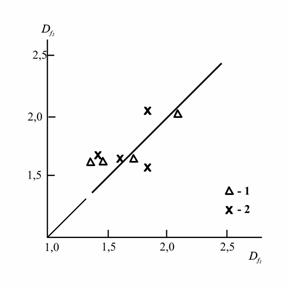
Рис.5.15. Сравнение фрактальных размерностей макромолекулярного клубка ![]() и
и ![]() , рассчитанных по соотношениям (3.10) и (2.9), соответственно, для процесса имидизации ПАК без наполнителя (1) и в присутствии 2вес.% Na+ -монтмориллонита (2) [37].
, рассчитанных по соотношениям (3.10) и (2.9), соответственно, для процесса имидизации ПАК без наполнителя (1) и в присутствии 2вес.% Na+ -монтмориллонита (2) [37].
Далее можно выполнить оценку параметра βd согласно уравнению (5.22) и сравнить его с предельной степенью конверсии Qпр, полученной экспериментально [2]. Такое сравнение для процесса имидизации ПАК без наполнителя и в присутствии 2вес.% Na+ -монтмориллонита при четырех указанных выше температурах имидизации выполнено на рис. 5.16. Получено достаточно хорошее соответствие теории и эксперимента (их среднее расхождение составляет ~12%), что подтверждает корректность предложенной трактовки [37].
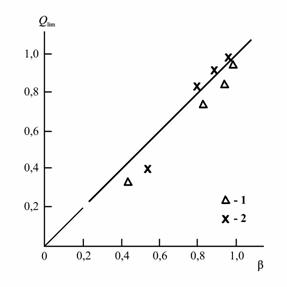
Рис. 5.16. Зависимость предельной степени имидизации Qпр от величины параметра βd для процесса имидизации ПАК без наполнителя (1) и в присутствии 2 вес.% Na+ -монтмориллонита (2) [37].
Следовательно, изложенные выше данные предполагают, что предельная степень конверсии (в рассматриваемом случае степень имидизации) определяется чисто структурным параметром-долей макромолекулярного клубка, подвергающейся эволюции (преобразованию) в ходе химической реакции. Эта доля может быть корректно оценена в рамках фрактального анализа. Для этой цели использована два метода расчета фрактальной размерности макромолекулярной клубка, которые дают согласованные результаты.
Известно, что большинство каталитических систем являются наполнителями [44]. При гетерогенном катализе активное вещество стараются нанести на носитель в виде наночастиц, чтобы увеличить их удельную поверхность. При гамогенном же катализе молекулы активного вещества часто сами по себе имеют нанометровые размеры. Известно также [2], что эксплутационные качества систем гетерогенного катализа зависят от их геометрии и структуры поверхности, которые могут сильно влиять на каталитические свойства, в частности, селективность (избирательность) катализа. Показано [27], что поверхность монтмориллонита является фрактальным объектом. Исходя из этого, ниже будет исследовано влияние фрактальной поверхности монтмориллонита на его каталитические свойства в реакции изомеризации.
В работе [47] были использованы два типа монтмориллонита - Na –монтмориллонит (SW) и Са – монтмориллонит (ST).
Указанные типы слоевого силиката применялись в качестве катализатора при изомеризации 1-бутена (Б) для получения цис-2-бутена (Ц) и транс-2 бутена (Т).
Микин [45] рассмотрел простейшую схему катализа, которая вследствии была использована для оценки селективности катализатора Sк. Она демонстрирует общие особенности, присущие всем моделям катализа, и выражена простой схемой реакции, которую по аналогии с реакциями (2.16)÷(2.21) можно записать так [46]:
А + П → Аа, (5.24)
![]() , (5.25)
, (5.25)
![]() , (5.26)
, (5.26)
где реакция (5.24) представляет адсорбцию молекулы А на поверхности катализатора П. Реакция (5.25) представляет унимолекулярный процесс, преобразующий адсорбированную молекулу А (Аа) в новую молекулу В, которая предполагается быстро покидающей поверхность катализатора. В реальных системах это может быть реакцией изомеризации (как в рассматриваемом случае) или реакцией распада побочных продуктов. Реакция (5.26) представляет собой присоединение молекулы А к поверхности катализатора в месте, уже занятом адсорбированной молекулой А (Аа) с последующей реакцией образования молекулы С, которая также предполагается быстро покидающей эту поверхность, чтобы сделать модель максимально простой. Селективность Sк определяется как число молекул С, деленное на число молекул В [45].
В рамках этой модели с использованием компьютерного моделирования было получено следующее выражение для Sк [45]:
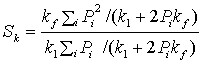 , (5.27)
, (5.27)
где kf – скорость поступления молекул А на поверхность катализатора , Pi – вероятность контакта для i-го места указанной поверхности.
Уравнение (5.27) существенно упрощается для двух предельных случаев. В пределе больших k1 оно принимает вид [45]:
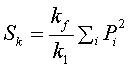 , (5.28)
, (5.28)
а в пределе малых k1 получим уравнение (2.24), в котором общее число мест поверхности N можно оценить согласно общему фрактальному соотношению [48]:
N~Ldn, (5.29)
где L-характерный размер частицы нанонаполнителя, принятым равным 100 им [2], dn-фрактальная размерность поверхности катализатора.
В свою очередь, величину dn можно оценить с помощью соотношения [49]:
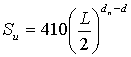 , (5.30)
, (5.30)
где Su - удельная поверхность частиц нанонаполнителя, d - размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d = 3). Величина Su дается в м2/г и L - в нм.
На рис.5.17 приведена зависимость Sk(N) для двух типов исследуемого катализатора-монтмориллонита. В случае реакции изомеризации 1-бутена уравнения (5.24)÷(5.26) можно переписать так [46]:
Б + П → Ба, (5.31)
![]() , (5.32)
, (5.32)
![]() , (5.33)
, (5.33)
и тогда величина S определяется как отношение Т/Ц.
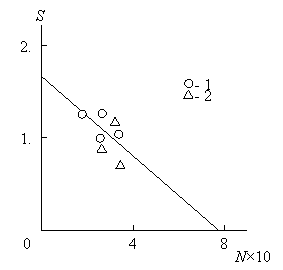
Рис.5.17. Зависимость селективности катализатора S от общего числа мест на его поверхности N для Na –монтмориллонита (1) и Са – монтмориллонита (2) [46].
Из данных рис. 5.17 следует линейное снижение Sk по мере роста N. Согласно уравнению (2.24) это предполагает протекание реакции изомеризации при малых k1 и при выполнении условия k1=const, kf= const или kf/k1= const. В случае больших k1 (уравнение (5.28)) ![]() >1/N [45]. Для кластеров Виттена-Сандера величина
>1/N [45]. Для кластеров Виттена-Сандера величина ![]() масштабируется так [45]:
масштабируется так [45]:
![]() ~N-γ, (5.34)
~N-γ, (5.34)
где показатель γ варьируется в пределах 0,5÷0,8 [45].
Одним из достоинств фрактального анализа является четкое определение предельных значений его основных характеристик- фрактальных размерностей. Так, величина dn изменяется в пределах 2≤ dn<3 [50]. При dn=2,0 величина N = 0,1х105 относительных единиц и, согласно графику рис. 5.17, максимальное значение Sk=1,65. При максимальной для реальных твердых тел размерности dn=2,95 [30] N=7,94х105 относительных единиц и согласно графику рис. 5.17 Sk→0. Это означает, что при таких условиях степень конверсии транс-2-бутена стремится к нулю.
Было обнаружено, что увеличение dn приводит к уменьшению общей степени конверсии транс-2-бутена и цис-2-бутена Q. Это объясняется тем, что формируемая в процессе синтеза полимерная цепь имеет конечную жесткость и состоит из статических сегментов конечной длины. В силу этого обстоятельства она не может «повторять» растущую по мере увеличения dn шероховатость поверхности катализатора и «воспринимает» ее как все более гладкую. В этом случае эффективная фрактальная размерность поверхности монтмориллонита dnэф определяется так [26]:
![]() (5.35)
(5.35)
в интервале ![]() =2,0÷2,5 и согласно уравнению (5.12) (при
=2,0÷2,5 и согласно уравнению (5.12) (при ![]() =
=![]() и
и ![]() =
=![]() ) в интервале 2,5÷3,0.
) в интервале 2,5÷3,0.
Поскольку для исследуемых катализаторов величины ![]() =2,637÷2,776 (отметим их близость к экспериментальной величине
=2,637÷2,776 (отметим их близость к экспериментальной величине ![]() =2,78 [27]), то для оценки
=2,78 [27]), то для оценки ![]() использовано уравнение (5.12). На рис. 5.18 приведена зависимость Q(
использовано уравнение (5.12). На рис. 5.18 приведена зависимость Q(![]() ), которая оказалась линейной и экстраполируется к Q=0 при
), которая оказалась линейной и экстраполируется к Q=0 при ![]() =2,0 (или
=2,0 (или ![]() =3,0) и к Q=1 при
=3,0) и к Q=1 при ![]() =
=![]() =2,5. Таким образом, совместное рассмотрение рис.5.17 и 5.18 позволяет предположить оптимальную величину
=2,5. Таким образом, совместное рассмотрение рис.5.17 и 5.18 позволяет предположить оптимальную величину ![]() катализатора, которая равна 2,5. При этом значении
катализатора, которая равна 2,5. При этом значении ![]() Q=1,0 и Sk = 1,54, т.е., близко к максимальной величине Sk, для монтмориллонита в рассматриваемой реакции.
Q=1,0 и Sk = 1,54, т.е., близко к максимальной величине Sk, для монтмориллонита в рассматриваемой реакции.
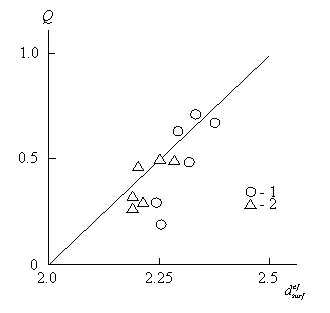
Рис. 5.18. Зависимость общей степени конверсии Q от эффективной фрактальной размерности ![]() поверхности катализатора для Na -монтмориллонита(1) и Са-монтмориллонита (2)[46].
поверхности катализатора для Na -монтмориллонита(1) и Са-монтмориллонита (2)[46].
Полимеризация in situ (совместно с нанонаполнителем) часто применяется как метод получения нанокомпозитов. В работе [51] процесс сшивания матричного эпоксиполимера как в присутствии нанонаполнителя (Na+ -монтмориллонита), так и без него был исследован в рамках концепции странной (аномальной) диффузии [52]. Сшивание нанокомпозитов эпоксиполимер/ Na+-монтмориллонит (ЭП/ММТ) выполнено при температурах 353, 373 и 333К, сшивание ЭП- при 393К [53].
Напомним основные положения концепции странной (аномальной) диффузии (более подробно см. главы 1 и 2). Как известно [52], в общем случае процессы диффузии описываются уравнением (сравните с формулой (2.38)):
<r2(t)>~tα, (5.36)
где <r2(t)> - среднеквадратичное смещение частицы за время t.
Если показатель α = 1, то соотношение (5.36) описывает классическую диффузию, а если ![]() - странную (аномальную) диффузию. В зависимости от конкретного значения α различают персистентные (супердиффузионные, 1<α≤2) и антиперсистентные (субдиффузионные, 0<α≤1) процессы. В уравнении странной диффузии параметр α имеет смысл фрактальной размерности «активного» времени, в котором реальные блуждания частиц как случайный процесс; интервал активного времени пропорционален tα [52]. В свою очередь, показатель β в этом же уравнении (2.39) учитывает мгновенные скачки частиц («полетов Леви») из одной области турбулентности в другую. Отношение показателей α/β можно определить из уравнения (2.39), в котором спектральная размерность ds определяется, в свою очередь, согласно уравнению (2.27).
- странную (аномальную) диффузию. В зависимости от конкретного значения α различают персистентные (супердиффузионные, 1<α≤2) и антиперсистентные (субдиффузионные, 0<α≤1) процессы. В уравнении странной диффузии параметр α имеет смысл фрактальной размерности «активного» времени, в котором реальные блуждания частиц как случайный процесс; интервал активного времени пропорционален tα [52]. В свою очередь, показатель β в этом же уравнении (2.39) учитывает мгновенные скачки частиц («полетов Леви») из одной области турбулентности в другую. Отношение показателей α/β можно определить из уравнения (2.39), в котором спектральная размерность ds определяется, в свою очередь, согласно уравнению (2.27).
Оценки показали [51], что введение ММТ в реакционную смесь существенно увеличивает величину ds: если для реакции без ММТ ds=0,027, то при введении ММТ ds повышается до 0,175÷0,452 и растет по мере повышения температуры сшивания. Фрактальную размерность макромолекулярного клубка (макрогеля) ЭП ![]() можно определить с помощью соотношения (3.10). Расчет согласно указанному соотношению показал, что наименьшая величина
можно определить с помощью соотношения (3.10). Расчет согласно указанному соотношению показал, что наименьшая величина ![]() , равная 1,52, получена для реакции сшивания без ММТ, а при введении ММТ она возрастает до 1,67÷2,19.
, равная 1,52, получена для реакции сшивания без ММТ, а при введении ММТ она возрастает до 1,67÷2,19.
Авторы [51] исходили из предложения, что зависимость Q от активного времени tα должна быть линейной и общей для всех четырех исследуемых реакций (см. рис. 2.31 и 4.11). Величина показателя β выбиралась на основании этого положения. Оказалось, что β уменьшается как при введении ММТ, так и при повышении температуры от 28 до 3,8. Кроме того, по мере протекания реакции сшивания без ММТ наблюдается снижение β от 28 до 9. На рис. 5.19 приведена зависимость Q(tα) для всех исследуемых реакций. Как можно видеть, получена общая линейная корреляция.
Активное время увеличивается при введении ММТ: для реакции без ММТ оно составляет ~2% от реального времени, а при наличии ММТ может достигать 30%.
На вставке рис. 5.19 показана зависимость β от ![]() , из которой следует снижение β по мере роста фрактальной размерности микрогеля. Это предполагает уменьшение вероятности «полетов Леви» по мере роста вязкости системы. Следовательно, умение контролировать активное время дает возможность управлять ходом реакции.
, из которой следует снижение β по мере роста фрактальной размерности микрогеля. Это предполагает уменьшение вероятности «полетов Леви» по мере роста вязкости системы. Следовательно, умение контролировать активное время дает возможность управлять ходом реакции.
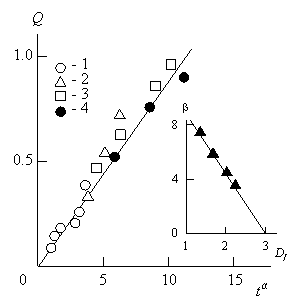
Рис. 5.19. Зависимость степени сшивания Q от активного времени tα для реакции без ММТ (1) и в присутствии ММТ при Т=353 (2), 373 (3) и 393К (4). На вставке: зависимость β(![]() ) [51].
) [51].
Литература к Главе 5
1. Васнев В.А., Нафадзокова Л.Х., Тарасов А.И., Виноградова С.В., Липендина О.Л. Высокомолек. соед. А, 2000, т. 42, № 12, с. 2065-2071.
2. Tyan H-L., Liu Y.-C., Wei K-H. Polymer, 1999, v. 40, № 11, p. 4877-4886.
3. Meakin P., Stanley H.E. J. Phys. A, 1984, v. 17, № 1, p. L173-L177.
4. Козлов Г.В., Шустов Г.Б. В сборн.: Успехи в области физико-химии полимеров. Ред. Заиков Г.Е. и др. М., Химия, 2004, с. 341-411.
5. Баранов В.Г., Френкель С.Я., Бресткин Ю.В. Доклады АН СССР, 1986, т. 290, № 2, с. 369-372.
6. Vilgis T.A. Physica A, 1988, т. 152, № 2, с. 341-354.
7. Rammal R., Toulouse G. J. Phys. Lett. (Paris), 1983, v. 44, № 1, p. L13-L22.
8. Нафадзокова Л.Х., Козлов Г.В., Заиков Г.Е. Теоретические основы химической технологии, 2007, т. 41, № 4, с.415-419.
9. Naphadzokova L. Kh., Kozlov G.V., Zaikov G.E. J. Appl. Polymer Sci., 2008 (в печати).
10. Копельман Р. В кн.: Фракталы в физике. Ред.Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 524-527.
11. Берштейн В.А., Егоров В.М. Дифференциальная сканирующая калориметрия в физикохимии полимеров. Л., Химия, 1990, 256 с.
12. Козлов Г.В., Новиков В.У.Успехи физических наук, 2001, т. 171, № 7, с. 717-764.
13. Kozlov G.V., Zaikov G.E. Structure of Polymer Amorphous State. Leiden-Boston, Brill Academic Publishers, 2004, 465 p.
14. Kozlov G.V., Dolbin I.V., Zaikov G.E. J. Appl. Polymer Sci., 2004, v. 94, № 4, p. 1353-1356.
15. Барнс Ф.С. Биофизика, 1996, т. 41, № 4, с. 790-802.
16. Sahimi M., Mc Karnin M., Nordahl T., Tirrell. M. Phys. Rev. A, v. 32, № 1, p. 590-595.
17. Нафадзокова Л.Х., Маламатов А.Х., Козлов Г.В. В сборн. научн. трудов молодых ученых, Нальчик, КБГУ, 2006, с. 305-307.
18. Новиков В.У., Козлов Г.В. Успехи химии, 2000, т. 64, № 4, с. 378-399.
19. Будтов В.П. Физическая химия растворов полимеров. СПб., Химия, 1992, 384 с.
20. Темираев К.Б., Козлов Г.В., Созаев В.А. Вестник КБГУ, физические науки, 1998, № 3, с. 24-28.
21. Липатов Ю.С. Межфазные явления в полимерах. Киев, Наукова думка, 1980, 260 с.
22. Пфейфер П.В. кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 72-81.
23. Козлов Г.В., Заиков Г.Е., Липатов Ю.С. Доклады НАН Украины, 2002, № 8, с. 130-135.
24. Нафадзокова Л.Х., Козлов Г.В., Заиков Г.Е. Пласт.массы, 2008 (в печати).
25. Козлов Г.В., Шустов Г.Б. Химическая технология, 2006, № 1, с. 24-26.
26. Van Damme H., Levitz P., Bergaya F. Alcover J.F., Gatineau L., Fripiat J.J. J. Chem. Phys., 1986, v. 85, № 1, p. 616-625.
27. Pernyeszi T., Dekany I. Colloid Polymer Sci., 2003, v. 281, № 1, p. 73-78.
28. Naphadzokova L.Kh., Kozlov G.V., Tlenkopachev M.A. 3-rd Intern. Symposium on Hybridized Materials with Super-Functions. Monterrey, Mexico, 3-6thDecember 2006, PM-06, p. 75.
29. Naphadzokova L. Kh., Kozlov G.V., Zaikov G.E. J. Balkan Tribologic. Assoc., 2007, v.13, N3, p.312-317.
30. Баланкин А.С. Синергетика деформируемого тела. М., Изд-во Министерства обороны СССР, 1991, 404 с.
31. Козлов Г.В., Сандитов Д.С., Липатов Ю.С. В кн.: Успехи в области физико-химии полимеров. Ред. Заиков Г.Е. и др. М., Химия, 2004, с. 412-474.
32. Сандитов Д.С, Бартенев Г.М. Физические свойства неупорядоченных структур. Новосибирск, Наука, 1982, 256 с.
33. Козлов Г.В., Алоев В.З. Теория перколяции в физико-химии полимеров. Нальчик, Полиграфсервиз и Т., 2006, 148 с.
34. Бобрышев А.Н., Козомазов В.Н., Бабин Л.О., Соломатов В.И. Синергетика композитных материалов. Липецк, НПО ОРИУС, 1994, 154 с.
35. Козлов Г.В., Нафадзокова Л.Х., Заиков Г.Е. Прикладная физика, 2007, № 4, с.52-55.
36. Kozlov G.V., Zaikov G.E. J. Balkan Tribologic Assoc., 2004, v. 10, № 1, p. 1-30.
37. Нафадзокова Л.Х., Козлов Г.В., Заиков Г.Е. Электр. журнал «Исследовано в России», 111, с.1173-1179, 2007.
38. Brady R.M., Ball R.C. Nature, 1984, v. 309, № 5965, p. 225-229.
39. Botet R., Jullien R., Kolb M. Phys. Red. A, 1984, v. 30, № 4, p. 2150-21-52.
40. Kobayashi M., Yoshioka T., Imai M., Itoh Y. Macromolecules, 1995, v. 28, № 22, p.7376-7385.
41. Kozlov G.V., Batyrova H.M., Zaikov G.E. J. Appl. Polymer Sci., 2003, v. 89, № 7, p. 1764-1767.
42. Нигматуллин Р.Р. Теоретическая и математическая физика, 1992, т. 90, № 3, с. 354-367.
43. Козлов Г.В., Шустов Г.Б. В сборн. трудов Междунар. междисциплинарного семинара «Фракталы и прикладная синергетика, ФиПС-01», М., Изд-во МГОУ, 2001, с. 155-157.
44. Мелихов И.В. Российский химический журнал, 2002, т. 66, № 5, с.7-14.
45. Meakin P. Chem. Phys. Lett., 1986, , v. 123, № 5, p. 428-432.
46. Нафадзокова Л.Х., Шустов Г.Б., Козлов Г.В. В сборн. трудов 9-го Международного симпозиума «Порядок, беспорядок и свойства оксидов, ОДРО-2006». Ростов-на-Дону, РГУ, 2006, с. 49-51.
47. Moronta A., Ferrer V., Quero J., Arteaga G., Choren E. Appl. Catalysis A, 2002, , v. 230, № 1, p.127-135.
48. Стенли Х. В кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 463-477.
49. Нафадзокова Л.Х., Афашагова З.Х.., Козлов Г.В. В сборн. cтат. V Междунар. научн.-практ. конф. «Эффективные строительные конструкции: теория и практика». Пенза, ПГУ, 2006, с. 271-273.
50. Avnir D., Farin D., Pfeifer P. Nature, 1984, , v. 308, № 5959, p. 261-263.
51. Нафадзокова Л.Х., Козлов Г.В. В сборн. стат Междунар. научн.-техн. конф. «Композиционные строительные материалы. Теория и практика». Пенза, ПГУ, 2006, с. 170-172.
52. Зеленый Л.М., Милованов А.В. Успехи физических наук, 2004, т. 174, № 8, с. 809-852.
53. Chen J-S., Poliks M.D., Ober C.K., Zhang Y., Wiesner U., Giannelis E. Polymer, 2002, v. 43, № 18, p. 4895-4904.
