
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Приложение 2. Полидисперсность наполнителей-катализаторов и законы синергетики
Полидисперсность используемых нанонаполнителей (слюды и оксида цинка) была определена на приборе Autosizer Tic фирмы «Мальверн» (Германия). Если предположить, что указанные наполнители являются наночастицами в строгом смысле этого термина, то следует изучить законы их формирования. Ранее на примере различных физико-химических процессов было показано, что функция самоподобия имеет вид функции итерационного типа, связывающей точки структурной бифуркации соотношением [1-3]:![]()
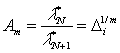 , (П.9)
, (П.9)
где ![]() -мера адаптивности
-мера адаптивности ![]() и
и ![]() - предыдущее и последующее критическое значение управляющего параметра при переходе от предыдущей (
- предыдущее и последующее критическое значение управляющего параметра при переходе от предыдущей (![]() ) к последующей
) к последующей ![]() ) точке бифуркаций;
) точке бифуркаций; ![]() -мера устойчивости, структуры, сохраняющаяся постоянной при ее перестройке; m-показатель типа обратной связи; значение m=1 отвечает линейной обратной связи, при которой переходы на другие пространственные уровни реализуется мультипликативным , а при m=2-репликативным (с улучшением структуры) механизмом воспроизведения структуры.
-мера устойчивости, структуры, сохраняющаяся постоянной при ее перестройке; m-показатель типа обратной связи; значение m=1 отвечает линейной обратной связи, при которой переходы на другие пространственные уровни реализуется мультипликативным , а при m=2-репликативным (с улучшением структуры) механизмом воспроизведения структуры.
Соотношение (П.9) по своей физической сути является алгоритмом самосборки наночастиц на пути к максимальной устойчивости. Этот алгоритм может быть представлен в виде [3]:
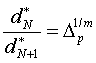 , (П.10)
, (П.10)
где ![]() и
и ![]() - интервалы размеров наночастиц, в пределах которых наноструктура остается устойчивой (
- интервалы размеров наночастиц, в пределах которых наноструктура остается устойчивой (![]() -const), m-параметр обратной связи (m=1 при линейной и m=2- при нелинейной обратной связи).
-const), m-параметр обратной связи (m=1 при линейной и m=2- при нелинейной обратной связи).
Сравнение экспериментальных и рассчитанных согласно уравнению (П.10) (при ![]() =0,618, m=2 и
=0,618, m=2 и ![]() = 930 нм) размеров частиц ZnO в этиленгликоле показало их хорошее соответствие (табл. П.1). То же можно сказать и о размерах частиц слюды двух типов (см. табл. П.2 и П.3), где расчет согласно уравнению (П.10) выполнен при следующих параметрах:
= 930 нм) размеров частиц ZnO в этиленгликоле показало их хорошее соответствие (табл. П.1). То же можно сказать и о размерах частиц слюды двух типов (см. табл. П.2 и П.3), где расчет согласно уравнению (П.10) выполнен при следующих параметрах: ![]() =0,465, m=4 и
=0,465, m=4 и ![]() = 920 нм.
= 920 нм.
Указанное соответствие предполагает формирование структуры частиц нанонаполнителей согласно законам синергетики, что позволяет считать их наночастицами. Отметим, что в настоящее время принято полагать, что верхний предельный размеров наночастиц равен 100 нм [4], хотя эта граница и является условной. Приведенные выше значения ![]() =920÷930 нм существенно увеличивают этот предельный размер, фактически до границы наноинтервала, т.е. 1000 нм.
=920÷930 нм существенно увеличивают этот предельный размер, фактически до границы наноинтервала, т.е. 1000 нм.
Таблица П.1.
Полидисперсность оксида цинка в этиленгликоле
| Размер частиц, нм | Размер частиц, нм уравнение (П.10) | Интенсивность, % |
| 100÷120 | 110 | 0,6 |
| 120÷150 | 135 | 5,8 |
| 150÷180 | 165 | 6,6 |
| 180÷220 | 200 | 7,5 |
| 220÷270 | 245 | 8,5 |
| 270÷320 | 295 | 8,3 |
| 320÷390 | 305 | 8,4 |
| 390÷470 | 430 | 8,9 |
| 470÷580 | 530 | 9,7 |
| 580÷700 | 640 | 10,8 |
| 700÷850 | 780 | 11,9 |
| 850÷1000 | 930 | 13,1 |
Средневероятностный размер-220 нм
Полидисперстность-0,398.
Таблица П.2.
Полидисперсность немодифицированной слюды «флагопит» в этиленгликоле
| Размер частиц, нм | Размер частиц, нм уравнение (П.10) | Интенсивность, % |
| 120÷150 | 136 | 5,0 |
| 150÷180 | 165 | 5,7 |
| 180÷220 | 200 | 6,3 |
| 220÷270 | 242 | 7,0 |
| 270÷320 | 292 | 8,0 |
| 320÷390 | 354 | 8,5 |
| 390÷470 | 428 | 8,9 |
| 470÷580 | 519 | 9,8 |
| 580÷700 | 628 | 11,2 |
| 700÷840 | 760 | 13,3 |
| 840÷1000 | 920 | 16,3 |
Средневероятностный размер-230 нм
Полидисперстность-0,749.
Таблица П.3.
Полидисперсность слюды - СМО в этиленгликоле
| Размер частиц, нм | Размер частиц, нм уравнение (П.10) | Интенсивность, % |
| 120÷150 | 136 | 5,7 |
| 150÷180 | 165 | 6,1 |
| 180÷220 | 200 | 6,9 |
| 220÷270 | 242 | 7,5 |
| 270÷320 | 292 | 8,1 |
| 320÷390 | 354 | 8,4 |
| 390÷470 | 428 | 8,9 |
| 470÷580 | 519 | 9,6 |
| 580÷700 | 628 | 10,9 |
| 700÷840 | 760 | 12,7 |
| 840÷1000 | 920 | 15,3 |
Средневероятностный размер-203 нм
Полидисперстность-0,733.
Литература к «Приложению 2»
1. Иванова В.С. Синергетика. Прочность и разрушение металлических материалов. М., Наука, 1992, 157 с.
2. Ivanova V.S. Synergetics, Strength and Fracturc of Metallic Materials. Cambridge international Science Publishers, 1998, 220 p.
3. Фолманис Г.Э. Самосборка частиц в свете особых свойств наномира. Труды Междунар. Междисциплинарного симпозиума «Фракталы и прикладная синергетика, Ф и ПС-03». М., Изд-во МГОУ, 2003, с. 303-308.
4. Бугаченко А.Л. Нанохимия-прямой путь к высоким технологиям нового века. Успехи химии, 2003, т. 72, №5, с. 419-437.
