Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Фрактальный анализ и синергетика катализа в наносистемах

Нафадзокова Л. Х., Козлов Г. В.,

1.5. Применение концепции странной диффузии для описания свойств полимерных материалов

Концепция странной (аномальной) диффузии представляет не только теоретический, но и практический интерес. Ее применение для описания химических реакций в наносистемах будет дано в последующих главах, а в настоящем разделе рассмотрено ее использование для описания термических свойств полимерных материалов и формирования межфазных слоев в полимерных композитах.

Как известно [91], температура интенсивной термодеструкции Т_d характеризует термостойкость полимеров. В качестве характеристики термостойкости согласно [92] применяется «предельная температура, при которой происходит химическое изменение полимера, отражающееся на его свойствах». Термостойкость определяется с помощью термогравиметрического анализа (ТГА). В дальнейшем под Т_d будет пониматься температура, определенная по пересечению касательных к двум ветвям термогравиметрической кривой [91].

Важность параметра T_d определила достаточно обширную литературу, посвященную исследованию зависимости T_d от характеристик полимеров кривой [91-95]. Тем не менее, эти исследования учитывают взаимосвязь T_d только с химическим строением полимера в том или ином варианте: наличие «слабых звеньев» [93], тех или иных групп в полимерной цепи [94], дефектов полимерной цепи [95] и т.д. Однако физическая структура полимерного материалов во всех этих исследованиях не учтена, хотя авторы [96] показали; что для пленок поликарбоната (ПК) на основе бисфенолаА, полученных из разных растворителей (что предполагает неизменность химического строения полимера) различие T_d может достигать 120 К. Этот результат предполагает сильное влияние структуры полимера при температуре испытаний на его термостойкость. В этом аспекте наиболее удобными объектами для исследования являются полимерные пленки, полученные из разных растворителей, и полимерные композиты. Для этих классов полимерных материалов возможны достаточно большие вариации их физической структуры без изменения химического строения полимера (полимерной матрицы). Поэтому авторы [97] исследовали влияние полимерных материалов на их термостойкость и получили аналитическую взаимосвязь T_d и структурных характеристик на примере пленок ПК, полученных из растворов в пяти разных растворителях и углепластиков на основе финилона [98].

Как правило, температура Т_d находится выше температуры так называемого перехода «жидкость 1- жидкость 2» Т_ее, которая может быть оценена следующим образом [99]:

  (1.60)

При Т_ее происходит переход полимерного расплава от жидкости с «фиксированной структурой (где наблюдается остаточная структурная упорядоченность) к истинно жидкому состоянию или «бесструктурной жидкости». Тем не менее, «бесструктурность» расплава относится к отсутствию надмолекулярной структуры, но структура макромолекулярного клубка в расплаве остается важным структурным фактором (по существу, единственным при Т> Т_ее) [99].

Наиболее точно структуру макромолекулярного клубка, который является фрактальным объектом [100], можно охарактеризовать с помощью его фрактальной (хаусдорфовой) размерности Δ_f. Эта размерность является истинной структурной характеристикой макромолекулярного клубка, поскольку она характеризует распределение его элементов в пространстве [101].

Для теоретической оценки температуры T_d авторы [97] использовали концепцию странной (аномальной) диффузии, применив для этой цели следующий вариант уравнения (1.8):

Δ_f = с (Т_d - Т_с) ^β,  (1.61)

где с-константа, методы определения, которой будут рассмотрены ниже.

Ранее в рамках теории дробных производных была показана взаимосвязь Δ_f и показателя β в уравнении (1.1), которая аналитически выражается следующим образом [9]:

  (1.62)

для медленной диффузии и

  (1.63)

для быстрой.

Структурной границей между указанными видами диффузии следует считать величину Δ_f <2,5 (менее компактные макромолекулярные клубки) реализуется быстрая диффузия оксиданта (кислорода), при Δ_f >2,5- медленная [97].

Уравнение (1.61) определяет три фактора, влияющих на термостойкость полимерных материалов: химическое строение полимера, характеризуемое величиной Т_с, структуру полимерного расплава, характеризуемого размерностью Δ_f, и тип (интенсивность) диффузии оксиданта, связанный со структурой и характеризуемым показателем β [97].

Рис.1.23. Сравнение эксперимен-тальной  и рассчитанной по уравнению (1.61)  температур интенсивной термодеструкции для углепластиков на основе фенилона (1) и пленок ПК (2)[97].

Как показали оценки константы С в уравнении (1.61) согласно методу наилучшего совмещения теории и эксперимента, эта константа имеет разные значения для разных полимеров и разных типов диффузии. Так, в случае углепластиков на основе фенилона с=0,20 для быстрой и 0, 50 для медленной диффузии, а в случае ПК-С=0,093

Для быстрой и 0,30-для медленной диффузии. Сравнение экспериментальных  и рассчитанных согласно уравнению (1.61)  с использованием указанных выше параметров значений температур интенсивной деструкции для двух полимерных материалов приведено на рис. 1.23. Как можно видеть, получено хорошее соответствие теории и эксперимента (среднее расхождение величин  и  составляет ~2%).

Анализ значений константы С в уравнении (1.61) показал их увеличение по мере роста Т_с полимеров (с учетом данных для композитов на основе полиарилата (ПАр) [102], наполненных короткими волокнами.

Это обстоятельство позволило построить зависимость С (Т_с) для случая быстрой диффузии, показанную на рис. 1.24. Аналитически эту зависимость можно записать так [97]:

.    (1.64)

Рис.1.24. Зависимость коэффициента С в уравнении (1.61) от температуры стеклования Т_с [97].

Уравнение (1.64) позволяет сделать ряд выводов. Во-первых, оно справедливо для полимеров, с относительно высокой (>350К) величиной Т_с. Во-вторых, увеличение Т_с приводит к росту С и, согласно уравнению (1.61) к уменьшению роли структуры в определении . В третьих, последнее обстоятельство объясняет более высокие значения С для медленной диффузии по сравнению с быстрой для одного и того же полимера: роль структурного фактора в случае медленной диффузии существенно меньше, что можно было предположить априори. С учетом уравнения (1.64) формулу (1.61) можно переписать следующим образом [97]:

,  (1.65)

что позволяет избежать разных значений константы для разных полимеров и типов диффузии.

На рис.1.25 приведено сравнение экспериментальных  и рассчитанных по уравнению (1.65)  температур интенсивной термодеструкции для пленок ПК, углепластиков на основе фенилона и стеклопластиков на основе ПАр. Как можно видеть, уравнение (1.65) дает достаточно точную оценку величины T_d (среднее расхождение  и составляет ~2,8%) в интервале T_d~160К.

И наконец, на рис. 1.26 показана зависимость отношения (T_d/Т_с) от Т_с, рассчитанная согласно уравнению (1.65). Как следует из графика рис. 1.26, отношение (T_d/Т_с) быстро стремится к единице или T_d→Т_с по мере роста Т_с и при Т_с ≈ 700 К различие T_d и Т_с находится в пределах погрешности расчета, т.е., <3%. Именно такое соотношение T_d и Т_с при изменении Т_с наблюдается экспериментально [91].

Следовательно, изложенные выше результаты показали важную роль структуры полимерного расплава в определении температуры интенсивной деструкции или термостойкости полимерных материалов. Последняя характеристика зависит от химического строения полимеров, выраженного через температуру стеклования, компактности макромолекулярного клубка в расплаве и типа аномальной диффузии оксиданта, который также определяется структурой [97].

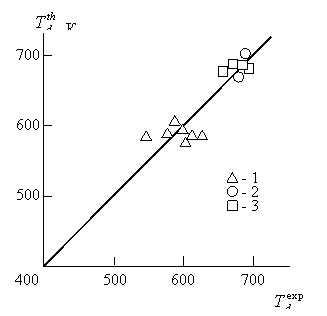
Рис.1.25.Сравнение экспериментальной  и рассчитанной по уравнению (1.65)  температур интенсивной деструкции для углепластиков на основе фенилона (1) и пленок ПК (2) и стеклопластиков на основе ПАр (3) [97].

Рис.1.26. Зависимость отношения (T_d/Т_с) от температуры стеклования Т_с, рассчитанная по уравнению (1.65). Вертикальная штриховая линия указывает условие T_d ≈Т_с [97].

Ранее было обнаружено [103], что введение высокодисперсной смеси Fe/FeO (Z) в ПЭВП приводит к существенному ( примерно на 100 К) повышению T_d по сравнению с исходным полимером. Поэтому авторы [104-106] исследовали влияние Z на термостойкость композиций ПЭВП+Z. В качестве теоретической базы исследований использована модель странной (аномальной) диффузии [107]. В формуле (1.61) вместо температуры T_d использован его аналог-температура 5%-й потери массы образца Т_5% в испытаниях ТГА.

На рис. 1.27 приведены теоретические зависимости Т_5% от содержания Z С_z для случаев медленной и быстрой диффузии оксиданта, а также экспериментальные значения Т_5% , полученные на воздухе и в атмосфере гелия. Как следует из данных этого рисунка, величина Т_5% для исходного ПЭВП соответствует случаю медленной диффузии, а для композиций ПЭВП+Z-быстрой диффузии. Обращает на себя внимание тот факт, что экспериментальные значения Т_5% выше теоретических и это расхождение растет по мере увеличения содержания Z. Для величин Т_5% , полученных в атмосфере гелия, где в силу отсутствия внешнего оксиданта процессы диффузии не играют какой-либо роли, выполняется условие Т_5% =const=708±4K, что и следовало ожидать.

Рассмотрим физические основы изменения режима диффузии от медленного (субдиффузионного) к быстрому (супердиффузионному). Аномальные (странные) процессы переноса описываются общим уравнением [107]:

,  (1.66)

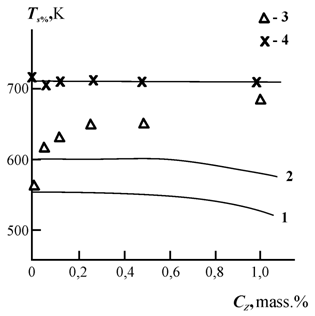
Рис.1.27. Зависимости температуры 5%-й потери массы Т_5% в испытаниях ТГА от содержания Z С_z для композиций ПЭВП+Z. Расчет по уравнению (1.61) для медленной (1) и быстрой (2) диффузии; Экспериментальные данные ТГА на воздухе (3) и в атмосфере гелия (4) [104].

где -характерный размер области, в которой побывает частица (молекула оксиданта) к моменту времениt, D_об-обобщенный коэффициент переноса. При 0≤μ<1 говорят о субдиффузионных процессах переноса, а при

1< μ ≤2- о супердиффузионных процессах.

Величина μ связана с индексом связанности q траектории блуждания молекулы оксиданта на структуре полимера следующим образом [107]:

.    (1.67)

Знак индекса связанности определяет топологию блуждания молекул оксиданта. Частицы Z являются ловушками или захватами для указанных молекул, прерывая их траекторию, вследстие чего структура полимера разбивается на ряд «подструктур» и блуждание молекулы оксиданта допускается только в пределах одной такой «подструктуры» до встречи с частицей Z. Это означает нарушение связанности траектории блуждания [107] и индекс q становится отрицательным. Тогда из уравнения (1.67) следует условие μ>1, т.е., наблюдается переход от субдиффузионного процесса переноса для исходного ПЭВП, где отсутствие частиц Z предполагает блуждание молекулы оксиданта по всей структуре полимера (до встречи с реакционноспособным центром макромолекулы) к супердиффузионному для композиций ПЭВП+Z.

Отметим, что расхождение температур Т_5% , рассчитанных согласно уравнению (1.61) для быстрой диффузии, и экспериментальных значений Т_5%(Δ Т_5% ) растет по мере увеличения содержания Z С_z (рис. 1.27).

На рис. 1.28 приведена зависимость Δ Т_5% от С_я , которая линеаризована использованием аргумента  и аналитически выражается следующим образом [105]:

Δ Т_5% =90С_z^1/2,  (1.68)

где Δ Т_5% дается в К, а С_z- в вес.%.

Обращает на себя внимание тенденция приближения экспериментальных значений Δ Т_5% к данным, полученным в атмосфере газа (гелия), наблюдаемая на рис. 1.27. Используя теоретическую кривую 2 этого рисунка (случай быстрой диффузии) и уравнение (1.68), можно оценить величинуC_z, при которой значения Т_5% для композиций ПЭВП+Z, полученные на воздухе и в атмосфере инертного газа, станут равны, т.е., все

молекулы оксиданта будут захвачены частицами Z. Такое условие реализуется при С_z≈3,5 вес.%. Из чисто геометрических соображений, используя экспериментально определенные размеры частиц Z[108], можно рассчитать, что при указанном содержании Z структура полимера будет разбита на «подструктуры» с характерным линейным размером ~1,5 мкм, в которых будет ограничено блуждание молекулы оксиданта, т.е., в пределах «своей» компоненты связанности [107].

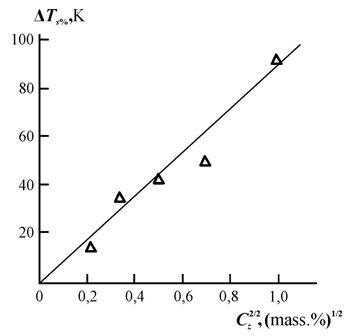
Рис.1.28. Зависимость величины расхождения экспериментальных и теоретических данных ТГА Δ Т_5% от содержания Z С_z для композиций ПЭВП+Z [104].

Таким образом, приведенные выше данные показали применимость фрактальной модели странной (аномальной) диффузии для количественного описания результатов ТГА и в случае композиций ПЭВП+Z. Обнаружено влияние типа диффузии на величину температуры 5%-й потери массы образца и дан структурный анализ этого эффекта [104-106].

Относительной особенностью полимерных композитов является наличие в них межфазных слоев, структура и свойства которых в значительной степени определяют свойства композита как конструкционного материала [109]. Поэтому исследованию данного вопроса всегда уделялось много внимания [110]. В последние годы для этой цели используются современные физические концепции: скейлинг, модели необратимой агрегации, фрактальный анализ т.д. [111, 112]. В рамках этих моделей было продемонстрировано существенное влияние на структуру межфазных слоев как структуры поверхности частиц (волокон) наполнителя, так и механизма их формирования, который связан со степенью участия в образовании указанных слоев диффузионных процессов [113-116]. В общем случае эту взаимосвязь можно сформулировать следующим образом: чем сильнее роль диффузионных процессов в формировании межфазного слоя, тем выше степень взаимопроникновения макромолекулярных клубков в нем и тем выше его прочность [113]. Исходя из этих общих постулатов, авторы [117] исследовали роль диффузионных процессов в формировании межфазных слоев в углепластиках на основе фенилона с привлечением теории дробных производных, фрактального анализа и концепции странной (аномальной) диффузии.

В рамках последней концепции величина показателя α была рассчитана двумя способами. Первый из них заключался в использовании уравнений (1.6) и (1.7). Второй метод расчета показателя α состоит в прямом применении соотношения (1.1) при условии, что толщина межфазного слоя l_мф равнаS, а величина t принимается равной продолжительности переработки композита. В рассматриваемом случае t=300с, а величина l_мф рассчитывалась из уравнения [118]:

 ,   (1.69)

где r-радиус волокна наполнителя, принятый равным 4 мкм, φ_н-объемная доля наполнения, равная 0,115 [119], а объемная доля межфазных слоев φ_нфопределена с использованием следующего уравнения [118]:

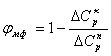,    (1.70)

где  и - величины скачка теплоемкости при постоянном давлении и температуры стеклования для композита и матричного полимера, соответственно.

Величину фрактальной размерности структуры межфазного слоя можно рассчитать согласно уравнению (1.22) при замене φ_кл на φ_мф [117].

На рис.1.29 приведено сравнение полученных теоретически и рассчитанных по уравнению (1.1) зависимостей β от. Как можно видеть, величины β, рассчитанные по уравнению (1.1), т.е., по экспериментальным значениям l_мф и t, являются промежуточными между теоретическими зависимостями β() для медленной и быстрой диффузии. Увеличение  приводит к снижению β и определяет переход от быстрой диффузии к медленной. В свою очередь, это приводит к уменьшению l_мф от 2,77 до 1,18 мкм.

Рис.1.29. Зависимость показателя β от фрактальной размерности структуры межфазного слоя для углепластиков на основе фенилона. Теоретический расчет для медленной(1) и быстрой(2) диффузии; расчет по уравнению (1.1) для образцов полученных с использованием магнитной (3) и механической (4) сепарации [117].

Чтобы выяснить физические основы этого эффекта, авторы [117] выполнили расчет радиуса инерции макромолекулярного клубка в межфазном слое. В рамках теории дробных производных этот параметр можно определить из уравнения [9]:

,    (1.71)

где -длина статистического сегмента, Г(α)-гамма-функция Эйлера, N-степень полимеризации.

Величина  определена согласно формуле [120]:

,     (1.72)

где -длина скелетной связи основной цепи, равная для фенилона 1,40? [121]. -характеристическое отношение.

Взаимосвязь между структурой конденсированного состояния межфазного слоя, характеризуемой размерностью  и фрактальной размерностью макромолекулярного клубка D_f для линейных полимеров дается так [122]:

 ,    (1.73)

А величина дробного показателя для такого клубка определяется следующим образом [123]:

,   (1.74)

где -фрактальная размерность «протекаемого» клубка равная ? 1,50 [124].

Гамма – функция Эйлера для переменной α имеет следующий вид [20]:

,   (1.75)

а величина N принята равной 200.

На рис. 1.30 приведена зависимость величины β, рассчитанной по уравнению (1.1), от радиуса инерции  макромолекулярного клубка. Как следует из данных этого радиуса, увеличение  или повышение степени растяжения клубка на поверхности волокна приводит к ослаблению диффузионных процессов, выраженному снижению β. Иначе говоря, чем сильнее растянут клубок на поверхности волокна, тем плотнее структура межфазного слоя и выше его фрактальная размерность , что приводит к ослаблению взаимопроникновения макромолекулярных клубков, подавлению диффузионных процессов и снижению β, в конечном итоге определяющим переход от быстрой диффузии к медленной.

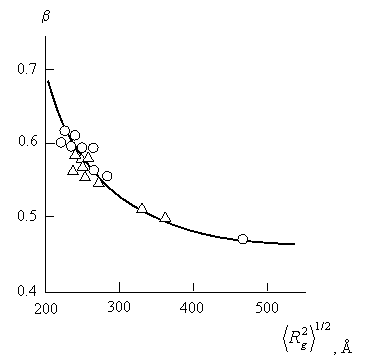
Рис.1.30. Зависимость показателя β от радиуса инерции  макромолекулярного клубка в межфазном слое для углепластиков на основе фенилона, полученных с применением магнитной (1) и механической(2) сепарации[117].

Рассмотрим влияние диффузионных процессов на прочность межфазного слоя σ_а. Этот параметр можно оценить из уравнения [125]:

, Па,   (1.76)

где N_A-число Авагадро, S- площадь поперечного сечения макромолекулы.

На рис. 1.31 показана зависимость σ_а от показателя β, рассчитанного по уравнению (1.1), из которой следует быстрый рост σ_а по мере увеличения β.

Следовательно, усиление роли диффузионных процессов при формировании межфазных слоев способствует повышению их прочности. Физическая основа этого эффекта очевидна- усиление диффузии способствует взаимопроникновению макромолекулярных клубков, формированию более плотной сетки физических зацеплений, что увеличивает прочность межфазного слоя [113].

Рис.1.31. Зависимость прочности межфазного слоя σ_а от величины показателя β для углепластиков на основе фенилона, полученных с использованием магнитной (1) и механической (2) сепарации [117].

Следовательно, рассмотренные выше данные продемонстрировали влияние структуры межфазных слоев на интенсивность диффузионных процессов, протекающих при их формировании. Увеличение фрактальной размерности структуры этих слоев, обусловленное растяжением структуры этих слоев, обусловленное растяжением макромолекулярных клубков на гладкой поверхности волокна, определяет переход от быстрой диффузии к медленной. Этот фактор контролирует как толщину межфазного слоя, так и его прочность [117].

Литература к Главе 1.

1. Рейтлингер С.А. Проницаемость полимерных материалов. М., Химия, 1974, 272 с.

2. Николаев Н.И. Диффузия в мембранах. М., Химия, 1980, 232 с.

3. Дубяга В.П., Перепечкин А.П., Каталевский В.Е. Полимерные мембраны. М., Химия, 1981, 232 с.

4. Волков В.В., Наметкин Н.С., Новицкий Э.Р., Дургарьян С. П. Высокомолек. соед. А, 1979, т. 21, №4, с. 920-926.

5. Kozlov G.V., Afaunov V.V., Mashukov N.I., Lipatov Yu.S In book: Fractals and Local Order in Polymeric Materials. Ed. Kozlov G., Zaikov G. New York, Nova Science Publishers, Inc., 2001, p. 143-149.

6. Kozlov G.V., Zaikov G.E. In book: Fractals Analysis of Polymers: From Synthesis to Composites. Ed Kozlov G., Zaikov G., Novikov V. New York, Nova Science Publishers, Inc., 2003, p. 107-112.

7. Афаунов В.В., Машуков Н. И., Козлов Г. В., Сандитов Д. С. Известия ВУЗов, Северо-Кавказск. регион, естествен. науки, 1999, № 4, с. 69-71.

8. Чукбар К.В. Журнал экспериментальной и теоретической физики, 1995, т. 108, № 5(11), с. 1875-1884

9. Шогенов В.Х., Ахкубеков А.А., Ахкубеков Р.А. Известия ВУЗов, Северо-Кавказск. регион, естествен. науки, 2004, № 1, с. 46-50.

10. Халиков Р.М., Козлов Г.В. Инженерная физика, 2005, № 3, с. 20-22.

11. Тепляков В.В., Дургарьян С.Г. Высокомолек. соед. А, 1984, т. 26, №7, с. 1498-1505.

12. Тепляков В.В., Дургарьян С.Г. Высокомолек. соед. А, 1986, т. 28, №3, с. 564-572.

13. Волков В.В., Гольданский А.В., Дургарьян С.Г., Онищук В.А., Шанторович В.П., Ямпольский Ю.П. Высокомолек. соед. А, 1987, т. 29, №1, с. 192-197.

14. Козлов Г.В., Заиков Г.Е. Высокомолек. соед. Б, 2003, т. 45, №7, с. 1197-1201.

15. Kozlov G.V., Zaikov G. E. J. Appl. Polymer Sci., 2004, v.92, №6, p. 3761-3763.

16. Kozlov G.V., Zaikov G. E. The Structural Stabilization of Polymers: Fractal Models. Leiden-Boston, Brill Academic Publishers, 2006, 345 p.

17. Alexander S., Orbach R. J. Phys. Lett. (Paris), 1982, v. 43, № 17, p. L625-L631.

18. Козлов Г.В., Афаунов В.В., Машуков Н.И., Липатов Ю.К. Доклады НАН Украины, 2000, № 10, с. 140-145.

19. Козлов Г. В., Шетов Р.А., Бажева Р.Ч., Тленкопачев М.А. Сборн. матер. Всероссийск. научн.-практ. конф. «Технологическое обеспечение качества машин и приборов». Пенза, ПГУ, 2004, с. 26-28.

20. Баланкин А.С. Синергетика деформируемого тела. М., Изд-во Министерства Обороны СССР, 1991, 404 с.

21. Козлов Г. В., Сандитов Д.С. Ангормонические эффекты и физико-механические свойства полимеров. Новосибирск, Наука, 1994, 261 с.

22. Халиков Р.М., Козлов Г.В., Шетов Р.А. Рукопись депонирована в ВИНИТИ РАН, Москва, 29. 05. 2006, № 718-В2006.

23. Сандитов Б.Д., Козлов Г.В., Сандитов Д.С., Липатов Ю.С. Матер. Всероссийск. научн. конф. «Математическое моделирование в синергетических системах». Улан-Удэ-Томск, ТГУ, 1999, с. 330-332.

24. Kozlov G.V., Zaikov G. E. In book: Fractal Anlysis of Polymers: From Synthesis to Composites. Ed Kozlov G., Zaikov G., Novikov V. New York, Nova Science Publishers, Inc., 2003, p. 141-178.

25. Козлов Г.В., Сандитов Д. C., Липатов Ю.С. В кн.: Успехи в области физико-химии полимеров. Ред. Заиков Г. и др. М., Химия, 2004, с. 412-474.

26. Jean Y.C., Sandreczki T.C., Ames D.P. J.Polymer Sci.: Part B: Polymer Phys., 1986, v. 24, № 6, p. 1247-1258.

27. Lin D., Wang S.J. J. Phys.: Condensed Matter, 1992, v.4, № 16, p. 3331-3336.

28. Hinkley J.A., Eftekhari A., Crook R.A., Jensen B. J., Singh J.J. J. Polymer Sci.: Part B: Polymer Phys., 1992, v. 30, № 11, p. 1195-1198.

29. Borek J., Osoba W. J. Polymer Sci.: Part B: Polymer Phys., 1996, v. 34, № 1, p. 1903-1906.

30. Шкловский Б.И., Эфрос А.Л. Успехи физических наук, 1995, т. 117, № 3, с. 401-436.

31. Халиков Р.М., Козлов Г.В. В сборн. стат. IV Всероссийск. научн.- практ. конф. «Инновации в машиностроении», Пенза, ПГУ, 2004, с. 101-104.

32. Sanchez I.C. J Appl Phys, 1974, v. 45, № 10, p. 4204-4215.

33. Роджерс К.Э. В кн.: Конструкционные свойства пластмасс. Ред. Бэр Э. М., Химия, 1967, с. 193-273.

34. Kluin J.-E., Vleeshouwers S., Mc. Gervey J.D., Jamieson A.M., Simha R. Macromolecules, 1992, v. 25, № 19, p. 5089-5093.

35. Kozlov G.V., Dolbin I.V., Zaikov G.E. Russian Polymer News, 2001, v. 6, № 4, p. 39-42.

36. Kozlov G.V., Zaikov G.E. In book: Monomer and Polymer Research Frontiers. Ed. D’Amore A., Zaikov G. New York, Nova Science Publishers, Inc., 2006, p. 89-95.

37. Яновский Ю. Г., Нафадзокова Л.Х., Козлов Г.В., Заиков Г.Е. Физическая мезомеханика, 2007, т. 10, № 4 , с.49-52.

38. Стенли Х. В кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 463-477.

39. Точин В.А., Шляхов Р.Ф., Сапожников Д.Н. Высокомолек. соед. А, 1980, т. 22, № 4, с. 752-758.

40. Соколов И.М. Успехи физических наук, 1986, т. 150, № 2, с. 221-256.

41. Козлов Г.В., Алоев В.З. Теория перколяции в физико-химии полимеров. Нальчик, Полиграф-сервис и Т, 2005, 148 с.

42. Козлов Г.В., Новиков В.У. Синергетика и фрактальный анализ сетчатых полимеров. М., Классика, 1998, 112 с.

43. Aharoni S.M. Macrmolecules, 1985, v. 18, № 12, p.2624-2630.

44. Будтов В.П. Физическая химия растворов полимеров. СПб., Химия, 1992, 384 с.

45. Wu S. J Appl. Polymer Sci., 1992, v. 46, № 4, p. 619-624.

46. 46.Козлов Г.В., Газаев М.Ф., Новиков В.У., Микитаев Ф.К. Письма в ЖТФ, 1996, т. 22, № 16, с. 31-38.

47. Meakin P., Coniglio A., Stanley H.E., Witten T.A. Phys. Rev. A, 1986, v. 34, № 4, p. 3325-3340.

48. Журков С.Н. Физика твердого тела, 1980, т. 22, № 21, с. 3344-3349.

49. Сандитов Д.С., Козлов Г.В. Физика и химия стекла, 1995, т. 21, № 6, с. 547-576.

50. Нигматуллин Р.Р. Теоретическая и математическая физика, 1992, т. 90, № 3, с. 354-362.

51. Новиков В.У., Козлов Г.В. Успехи химии, 2000, т. 69, № 4, с. 378-399.

52. Новиков В.У., Козлов Г.В. Успехи химии, 2000, т. 69, № 6, с. 572-599.

53. Козлов Г.В., Новиков В.У. Успехи физических наук, 2001, т. 171, № 7, с. 717-764.

54. Козлов Г. В., Нафадзокова Л. Х., Заиков Г. Е. Прикладная физика, 2007, № 4, с. 52-55.

55. Белоусов В.Н., Белошенко В.А., Козлов Г.В., Липатов Ю.С. Украинский химический журнал, 1996, т. 62, № 1, с. 62-65.

56. Kozlov G. V., Zaikov G.E. Structure of the Polymer Amorphous State. Leiden-Boston, Brill Academic Publishers, 2004, 465 p.

57. Kozlov G. V., Batyrova H.M., Zaikov G.E J. Appl. Polymer Sci., 2003, v. 89, № 7, p. 1764-1767.

58. Федер Е. Фракталы. М., Мир, 1991, 248 с.

59. Boyer R.F. J. Macromol. Sci.-Phys, 1973, v.87, № 3, p. 487-501.

60. Kozlov G. V., Zaikov G.E In book: Fractals and Local Order in Polymeric Mterials. Ed. Kozlov G., Zaikov G. New York, Nova Science Publishers, Inc., 2001, p. 55-63.

61. Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. Новосибирск, Наука, 1982, 256 с.

62. Hayakawa Y., Sato S., Matsushita M. . Phys. Rev. A, 1987, v. 36, № 4, p. 1963-1966.

63. Kozlov G. V. In book: New Perspectives in Chemistry and Biochemistry. Ed. Zaikov G. New York, Nova Science Publishers, Inc., 2002, p. 57-65.

64. Brady R.M., Ball R.C. Nature, 1984, , v. 314, № 5965, p. 225-229.

65. Meakin P., Stanley H.E. Phys. Rev. Lett, 1983, v. 51, № 16, p. 1457-1460.

66. Rammal R., Toulouse G. J. Phys. Lett. (Paris), 1983, v. 44, № 1, p. L13-L22.

67. Козлов Г.В., Новиков В.У. Материаловедение, 1999, № 7, с. 22-24.

68. Козлов Г.В., Белошенко В.А., Варюхин В.И., Новиков В.У. Журнал физических исследований, 1997, т. 1, № 2, с. 204-207.

69. Halsey T.C., Jensen M.H., Kadanoff L.P., Procaccio I., Shraiman B.I. Phys. Rev. A, 1986, v. 33, № 2, p. 1141-1151.

70. Mc Cauley J.L. Intern. J. Modern Phys. B, 1989, , v. 3, № 6, p. 821-852.

71. Williford R.E. Scr. Metal, 1988, , v. 22, № 11, p. 1749-1754.

72. Новиков В.У., Козлов Г.В., Билибин А.В. Материаловедение, 1998, № 10, с. 14-19.

73. Kozlov G. V., Afaunova Z.I., Zaikov G.E. Oxidation Commun., 2005, v. 28, № 4, p. 856-862.

74. Kozlov G.V., Afaunova Z.I., Zaikov G.E. In book: Theoretical and Practical Guide to Organic Physical Chemistry. Ed. Zaikov G., Kozlov G., Makitra R. New York, Nova Science Publishers, Inc., 2006, p. 13-19.

75. Халиков Р.М., Козлов Г.В. Высокомолек. соед. Б, 2006, т. 48, № 4, с. 699-703.

76. Козлов Г.В., Бажева Р.И., Тленкопачев М.А., Ольховая Г.Г. Сборн. стат. VI Междунар. научн.-практ. конф. «Экология и жизнь». Пенза, ПГУ, 2003, с. 27-29.

77. Старанникова Л.Э., Тепляков В.В., Кожухова И.Н., Дургарьян С.Г. Высокомолек. соед. Б, 1989, т. 32, № 7, с. 526-530.

78. Халиков Р.М., Долбин И.В., Козлов Г.В. Матер. Междунар. научн. Конф «Молодежь и химия», Красноярск, КГУ, 2004, с. 197-199.

79. Kozlov G.V., Beloshenko V.A., Varyukhin V.N., Lipatov Yu.S. Polymer, 1999, v. 40, № 4, p. 1045-1051.

80. Халиков Р.М., Козлов Г.В. Успехи современного естествознания, 2005, № 1, с. 31-32.

81. Ash R., Barrer R.M., Palmer D.G. Polymer, 1970, v. 11, № 8, p. 421-430.

82. Kanitz P.J., Huang R.Y.M. J. Apll. Polymer Sci., 1971, v. 15, № 1, p. 67-82.

83. Хавлин С.В. кн.: Фракталы в физике. Ред. Пьетронеро Л., Тозатти Э. М., Мир, 1988, с. 498-506.

84. Kozlov G.V., Mashukov N.I., Zaikov G.E. In book: Aging of Polymers Polymer Blends and Polymer Composites. V.2. Ed. Zaikov G., Buchachenko A., Ivanov V. . New York, Nova Science Publishers, Inc., 2002, p. 139-144.

85. Халиков Р.М., Козлов Г.В., Алоев В.З. Обозрение прикладной и промышленной математики, 2004, т. 11, № 4, с. 951.

86. Khalikov R.M., Kozlov G.V., Zaikov G.E. J. Appl. Polymer Sci., 2006, v. 99, № 6, p. 3571-3573.

87. Majumdar S.N., Privman v. j. Phys. A, 1993, v. 26, № 7, p. L743-L748.

88. Халиков Р.М., Долбин И.В., Козлов Г.В., Ольховая Г.Г. Сборн. стат. VIII Всероссийск. научн.-практ. конф. «Современные технологии в машиностроении». Пенза, ПГУ, 2004, с. 108-111.

89. Argyrakis P., Kopelman R. Chem. Phys., 2000, v. 261, № 3, p. 391-398.

90. Аскадский А.А. Структура и свойства теплостойких полимеров. М., Химия, 1981, 320 с.

91. Коршак В.В. Химическое строение и температурные характеристики полимеров. М., Наука, 1970, 419 с.

92. Ван Кревелен Д. Свойства и химическое строение полимеров. М., Химия, 1976, 414 с.

93. Сазонов Ю.Н., Кудрявцев В.В., Светличный В.М., Федорова Г.Н., Антонова Т.А., Александрова Е.П. Высокомолек. соед. А, 1983, т. 25, № 5, с. 975-978.

94. Микитаев А.К., Берикетов А.С., Коршак В.В., Таова А.Ж. Высокомолек. соед. А, 1983, т. 25, № 8, с. 1691-1696.

95. Долбин И.В., Козлов Г.В., Бажева Р.Ч., Шустов Г.Б. Сборн. стат. V Всроссийской научн.-техн. конф. «Новые химические технологии: производство и применение». Пенза, ПГУ, 2003, с. 42-45.

96. Долбин И.В., Буря А.И., Козлов Г.В. Теплофизика высоких температур, 2007, т. 45, № 3, с. 355-358.

97. Соколов А.Б., Кузнецов Г.А., Герасимов В.Д. Пластмассы, 1967, № 9, с. 21-23.

98. Берштейн В.А., Егоров В.М. Дифференциальная сканирующая калориметрия в физикохимии полимеров. Л., Химия, 1990, 256 с.

99. Vilgis T.A. Physica A, 1988, v. 153, № 2, p. 341-354.

100. Иванова В.С., Кузеев И.В., Закирничная М.М. Синергетика и фракталы. Универсальность механического поведения материалов. Уфа, Изд-во УГНТУ, 1998, 366 с.

101. Долбин И.В., Буря А.И., Козлов Г.В. Фундаментальные исследования, 2005, № 3, с. 39-41.

102. Машуков Н.И., Сердюк В.Д., Козлов Г.В., Овчаренко Е.Н., Гладышев Г.П., Водахов А.Б. Стабилизация и модификация полиэтилена акцепторами кислорода. (Препринт). М., ИХФ АН СССР, 1990, 64 с.

103. Маламатов А.Х., Козлов Г.В., Лигидов М.Х., Пахомов С.И. Известия ВУЗов, Химия и химическая технология, 2006, т. 49, № 4, с. 62-65.

104. Malamatov A. Kh., Kozlov G.V. J. Balkan Tribologic Assoc., 2006, v.12, № 2, p. 192-197.

105. Маламатов А.Х., Козлов Г.В. Сборн. стат. Междунар. научн.-техн. конф. «Проблемы исследования и проектирования машин». Пенза, ПГУ, 2005, с. 163-165.

106. Зеленый Л.М., Милованов А.В. Успехи физических наук, 2004, т. 174, № 8, с. 809-852.

107. Машуков Н.И., Гладышев Г.П., Козлов Г.В. Высокомолек. соед. А, 1991, т. 33, № 12, с. 2538-2546.

108. Липатов Ю.С. Физико-химические основы наполнения полимеров. М., Химия, 1991, 259 с.

109. Липатов Ю.С. Межфазные явления в полимерах. Киев, Наукова думка, 1980, 260 с.

110. Новиков В.У., Козлов Г.В., Бурьян О.Ю. Механика композитных материалов, 2000, т. 36, № 1, с. 3-32.

111. Козлов Г.В., Яновский Ю.Г., Липатов Ю.С. Механика композиционных материалов и конструкций, 2002, т. 8, № 1, с. 111-149.

112. Schnell R., Stamm M., Creton C. Macromolecules, 1998, v. 31, № 7, p. 2284-2292.

113. Буря А.И., Шогенов В.Н., Козлов Г.В., Холодилов О.В. Материалы. Технологии. Инструменты, 1999, т. 4, № 2, с. 39-41.

114. Алоев В.З., Козлов Г.В. Физика и техника высоких давлений, 2001, т. 11, № 1, с. 40-42.

115. Маламатов А.Х., Козлов Г.В., Антипов Е.М., Микитаев М.А. Перспективные материалы; 2006, № 5, с. 54-58.

116. Kozlov G.V., Burya A. I., Dolbin I. V., Zaikov G.E. J. Appl. Polymer Sci., 2006, v. 101, № 6, p. 4044-4047.

117. Липатов Ю.С. Физическая химия наполненных полимеров. М., Химия, 1977, 304 с.

118. Козлов Г.В., Буря А.И., Долбин И.В. Прикладная физика, 2006, № 1, с. 14-18.

119. Wu S. J. Polymer Sci.: Part B: Polymer Phys., 1998, v. 27, № 4, p. 723-741.

120. Aharoni S.M. Macromolecules, 1983, v. 16, № 9, p. 1722-1728.

121. Kozlov G.V., Temiraev K.B., Shustov G. B., Mashukov N.I. J. Appl. Polymer Sci., 2002, v. 85, № 6, p. 1137-1140.

122. Козлов Г.В., Шустов Г.Б. Матер. Междунар. междисциплинарного семинара «Фракталы и прикладная синергетика. ФиПС-01» М., Изд-во МГОУ, 2001, с. 155-157.

123. Баранов В.Г., Френкель С.Я., Бресткин Ю.В. Доклады АН СССР, 1986, т. 290, № 2, с. 369-372.

124. Новиков В.У., Козлов Г.В., Шустов Г.Б., Липатов Ю.С. Пласт. массы, 2003, № 10, с. 4-8.