Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Фрактальный анализ и синергетика катализа в наносистемах

Нафадзокова Л. Х., Козлов Г. В.,

2.3. Фрактальная физика модельной реакции переэтерификации.

В последние годы стало очевидно, что в процессах химических реакций (особенно связанных с полимерами) важную роль играют структурные аспекты, как компонентов указанных реакций, так и реакционной среды [4-7]. Эта роль часто не меньше, а то и больше, чисто химических аспектов реакции. В настоящем разделе роль структуры будет рассмотрена для модельной реакции переэтерификации.

Влияние структуры продукта реакции переэтерификации (молекулы гептилбензоата) на её кинетику, а точнее, на величину k₁ можно описать следующим образом [5]. Указанную структуру можно охарактеризовать с помощью размерности (евклидовой или фрактальной) молекулы гептилбензоата D_f, описывающей распределение элементов молекулы в пространстве [12]. Формальная кинетика химических реакций первого порядка может быть описана следующим уравнением [13]:

,  (2.7)

где Q – степень конверсии (завершённости) реакции.

Общее фрактальное соотношение, также используемое для описания кинетики химических реакций, имеет вид [14]:

.    (2.8)

Дифференцируя соотношение (2.8) по времени t и приравнивая производную dQ/dt к аналогичной производной в уравнении (2.7), получим [14]:

,    (2.9)

где с₁ – константа, определяемая из граничных условий и принятая равной для исследуемых реакций 8х10^-4с^-1.

Сначала рассмотрим корректность описания модельной реакции переэтерификации как реакции первого порядка, для чего используем скейлинговый подход [15]. Обычно считается, что, если концентрация реагентов достаточно велика или процесс протекает с интенсивным перемешиванием, то он может рассматриваться как реакция первого порядка. В этом случае закон спадания концентрации реагентов со временем с (t) имеет вид [15]:

с(t) ≈ exp (-At)   (2.10)

Рис.2.3. Зависимости (1-Q) от продолжительности t в логарифмических координатах, соответствующие уравнению (2.10), для реакции переэтерификации без слюды (1) и в присутствии НМС (2), СМО (3), СМК (4) [16]

где А – константа, пропорциональная концентрации реакционноспособных мест реагентов.

На рис.2.3 приведены зависимости с (t), где с = (1-Q), соответствующие уравнению (10), для исследуемых реакций переэтерификации. Линейность этих зависимостей, т.е., соответствие скейлинговому закону (2.10), подтверждает, что реакция переэтерификации имеет первый порядок.

Далее для анализа структуры молекулы гептилбензоата авторы [16] сделали предположение, что ее размерность D_f может быть равна четырем значениям: 0; 1,0; 1,5 или 2,0. Иначе говоря, предполагается, что молекула гептилбензоата может быть аналогом точки, короткого стержня, протекаемого клубка или клубка в идеальном Θ-растворителе, соответственно [17]. Далее был выполнен расчет теоретического значения k₁ согласно уравнению (2.9) и сравнение его результатов с соответствующими экспериментальными значениями в форме функции k₁(t). Такое сравнение приведено на рис. 2.4 для реакции метилбензоата и гептанола-1 в присутствии НМС, а на рис. 2.5-для этой же реакции в присутствии СМК. Константа с₁ в указанном уравнении выбрана совмещением теоретического и экспериментального значений k₁ при минимальной продолжительности реакции t

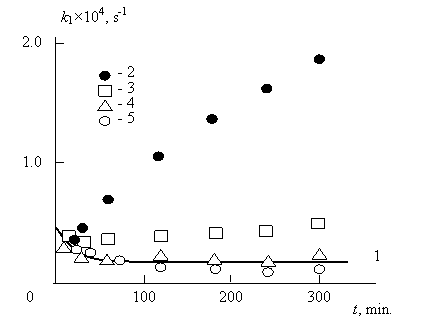
Рис.2.4. Зависимости константы скорости k₁ от продолжительности переэтерификации t в присутствии НМС. 1-экспериментальные данные; 2÷5 – расчет по уравнению (2.9) при D_f:0 (2), 1,0 (3), 1,5 (4) и 2,0 (5) [16]

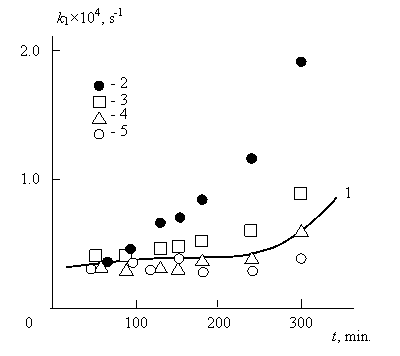
Рис. 2.5. Зависимости константы скорости k₁ от продолжительности переэтерификации t в присутствии СМК. 1-экспериментальные данные; 2÷5 – расчет по уравнению (2.9) при D_f : 0 (2), 1,0 (3), 1,5 (4) и 2,0 (5)[16].

и равна приведенной выше величине 8х10^-4с^-1. Фрактальная модель кинетики поликонденсации [4, 5] предполагает, что чем меньше D_f (чем сильнее открыта структура), тем быстрее протекает реакция. Из данных рис.2.4 и 2.5 следует, что в случае _.D_f=0 и D_f=1,0 зависимости k₁(t) не согласуются с экспериментом-величина k₁ растет гораздо быстрее, чем наблюдается экспериментально. Это означает, что наиболее простые структурные формы для молекулы гептилбензоата (точка и короткий одномерный стержень) не соответствуют действительности.

Использование размерности D_f=2,0 дает более медленный рост функции k₁(t) по сравнению с экспериментом (рис. 2.5) или ее более быстрое снижение (рис.2.4). Наиболее точное соответствие с экспериментальной функцией k₁(t) получено при использовании D_f=1,5 как качественное, так и количественное. Качественное соответствие заключается в точном теоретическом описании поведения функции k₁(t): увеличения k₁ по мере роста t в случае применения НМС (рис. 2.4). Количественное соответствие, в указанных случаях также достаточно хорошее (среднее расхождение теории и эксперимента не превышает 20%), которое к тому же может быть значительно улучшено более точным выбором величины D_f. Следовательно, выполненные выше оценки, предполагают, что молекула гептилбензоата представляет собой фрактальный (а точнее, фракталоподобный, поскольку низкая молекулярная масса указанной молекулы не допускает свойства самоподобия [18]) объект с размерностью, близкой к 1,50, т.е., ее структура близка к таковой для протекаемого макромолекулярного клубка [17]. Это обстоятельство делает обязательным учет структурного фактора при описании кинетики процесса переэтерификации (см. уравнение (2.9)) [4,5].

Рассмотрим физические основы формирования фрактальной структуры молекулы гептобензоата, которая имеет следующее химическое строение [16].

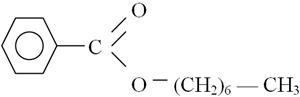
Это молекула состоит из 30 атомов и формируется реакцией не отдельных атомов, а нескольких фрагментов, каждый из которых состоит из нескольких атомов. Как известно [4,5], макромолекулярные клубки в процессе поликонденсации формируются согласно механизму необратимой агрегации кластер-кластер, т.е., объединением (агрегацией) мелких клубков в более крупные. В случае диффузионно-лимитированного механизма кластер-кластер размерность макромолекулярного клубка равна ~1,78 [19]. Уменьшение числа частиц в кластере (или атомов в макромолекулярном клубке) приводит к снижению D_f . Так, для случая двухмерного евклидова пространства снижение числа частиц в кластере от 64 до 1, 32, т.е., в 1,16 раз [19]. Если предположить такое же снижение D_f для гептилбензоата, то мы получим уменьшение D_f от 1,78 для макромолекулярного клубка полибутилентерефталата (высокомолекулярный аналог) до 1,53 для молекулы гептилбензоата (низкомолекулярный аналог), что хорошо согласуется с вышеприведенными данными.

Следовательно, рассмотренные выше результаты показали, что молекула продукта модельной реакции переэтерификации (гептилбензоата) имеет фракталоподобную структуру с размерностью, близкой к размерности протекаемого клубка, т.е., ~1,50. Это означает, что структура молекулы гептилбензоата существенно отличается от простых структурных форм (точки или короткого стержня). По существу, эта структура представляет собой начальный кластер для механизма агрегации кластер-кластер. Это обстоятельство определяет очень сильное влияние структуры молекулы гептилбензоата на кинетику процесса переэтерификации (см. рис 2.4 и 2.5). Как показано выше (см. табл. 2.1), введение слюды (как необработанной, так и модифицированной) существенно изменяет кинетику реакции переэтерификации. Особенно значительно отличие величины k₁ для переэтерификации в присутствии СМК: при продолжительности реакции t=300 мин величины k₁ равны 1,8; 1,5; 5,6 и 1,2с^-1 для реакций без слюды и в присутствии слюды НМС, СМК и СМО, соответственно.

Расчет величины D_f по уравнению (2.9) при t=300 мин и с₁=8х10^-4с^-1 для молекул гептилбензоата дал следующие результаты: 1,640; 1,710; 1,738 и 1,480 для реакции переэтерификации без слюды и в присутствии НМС, СМО и СМК, соответственно. Как отмечалось выше, из этих оценок следует, что молекулы гептилбензоата для всех четырех рассматриваемых реакций переэтерификации является фрактолоподобными объектами, чья структура, характеризуемая величиной D_f, существенно влияет на кинетику указанных реакций.

Авторы [20,21] показали, что эффективное число реакционноспосбных центров молекулы А зависит от ее структуры. Теоретическую величину А (А^Т) можно рассчитать следующим образом. Из фракталоподобия молекул гептилбензоата следует, что реакцию переэтерификации можно представить в виде «чертовой лестницы» [22,23]. Ее горизонтальные отрезки соответствуют временным интервалам, где реакция не идет. В этом случае реакция описывается с использованием фрактального времени, которое принадлежит точкам канторова множества [24]. Если же реакция рассматривается для евклидовых объектов, то время принадлежит множеству действительных чисел.

Для описания эволюционных процессов с фрактальным временем используется математический аппарат дробного дифференцирования и интегрирования [25, 26]. Как показано в работе [24], в этом случае дробный показатель ν_dp совпадает с фрактальной размерностью множества Кантора и указывает на долю состояний системы, сохранившихся за все время эволюции t. Напомним, что множество Кантора рассматривается в одномерном евклидовом пространстве и поэтому его фрактальная размерность d_f <1 в силу определения фрактала [27]. Для фрактальных (фракталоподобных) объектов в евклидовых пространствах с более высокими размерностями в качестве n_др следует принимать дробную часть d_f (в нашем случае – D_f) или [21]:

ν_dp= D_f – 1.  (2.11)

Тогда величина ν_dp характеризует долю фрактала (молекулы), не задействованную в ходе химических превращений.

Можно предположить, что величина А^Т или эффективное число реакционноспособных центров молекулы пропорционально доле структуры, подвергающейся химическим превращениям, или (1- ν_dp). Такое предположение позволило авторам получить следующее уравнение:

А^Т = 0,5(4-5 ν_dp)   (2.12)

На рис. 2.6 приведено сравнение величин А, определенных по наклону прямых рис. 2.3, и А^Т, рассчитанных согласно уравнению (2.12) (в обоих случаях число реакционноспособных центров дается в относительных единицах). Как можно видеть, между А и А^Т получено линейная корреляция, проходящая через начало координат. Это означает, что величина А, контролирующая кинетику реакции переэтерификации (см. уравнение (2.10)), полностью определяется структурой молекулы гептилбензоата, а роль поверхности слюды сводится к изменению величины D_f в ту или иную сторону. Этот вывод подтверждает зависимость k₁(А), приведенная на рис. 2.7, которая также линейна и проходит через начало координат. При А = 0 реакция прекращается (k₁ = 0). Определить величину D_f, соответствующую А = 0, можно из уравнения (2.11) и (2.12): D_f = 1,8. Это означает, что по мере приближения структуры молекулы гептилбензоата к клубку в идеальном (Θ) растворителе все реакционноспособные центры, находящиеся во внутренней части молекулы, становятся недоступными и реакция идти не может [28].

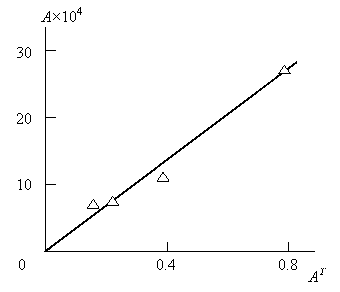
Рис.2.6. Сравнение числа реакционноспособных центров молекулы гептилбензоата А, рассчитанного из уравнения (2.10) и А^Т, полученного согласно уравнению (2.12) (в относительных единицах) [28].

 Рис. 2.7. Зависимость константы скорости реакции k₁ от числа реакционноспособных центров молекулы гептилбензоата А для реакции переэтерификации [28].

Рассмотрим физические причины снижения D_f молекулы гептилбензоата в случае присутствия СМК. Как отмечалось в предыдущем разделе, исследования методом рентгенофотоэлектронной спектроскопии показали, что для СМК, в отличие от НМС и СМО, наблюдается снижение поверхностной концентрации металлов и рост концентрации кремния, что может привести к усилению взаимодействия молекул реагентов и поверхности слюды. Таким образом, в случае СМК выполняются два основных условия снижения D_f на поверхности твердого тела: сильные взаимодействия молекулы–гостя и поверхности (с учетом жесткости не цепной молекулы гептилбензоата и ее компонентов) и гладкая (близкая к плоской с размерностью 2) форма (структура) поверхности частиц слюды [29].

Следовательно, изложенные выше результаты показали, что кинетика модельной реакции переэтерификации полностью определяется фракталоподобной структурой продукта этой реакции- молекулы гептилбензоата и составляющих ее компонентов. Роль поверхности наполнителя (слюды) сводится к изменению, фрактальной размерности указанной молекулы в ту или иную сторону. Это еще раз подчеркивает определяющую роль межфазных явлений для любых многофазных систем и наносистем в особенности [30].

Далее рассмотрим зависимость степени конверсии Q от структуры молекулы гептилбензоата, характеризуемой размерностью D_f. Авторы [31] предложили обобщенную модель, позволяющую получить указанную зависимость. На рис. 2.8 приведена зависимость Q от обобщенного аргумента А^Тt, которая аппроксимируется общей прямой для четырех исследуемых реакций переэтерификации. Аналитически ее можно выразить так [31]:

Q =2,2 х 10^-5 (9-5D_f) t,  (2.13)

где t дается в с, а множитель (9-5D_f) получен из сочетания уравнений (2.11) и (2.12).

Рис.2.8. Зависимость степени конверсии Q от обобщенного аргумента А^Тt для реакции переэтерификации без слюды (1) и в присутствии НМС (2), СМО (3), СМК (4). [31]

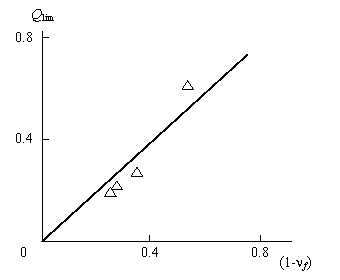
Рис.2.9. Соотношение между предельной степенью конверсии Q приt = 300 мин и дробным показателем (1-ν_dр) для исследуемых реакций переэтерификации.

Следовательно, данные рис. 2.8 подтверждают, что кинетика реакции переэтерификации полностью определяется структурой молекулы гептилбензоата, а роль слюды сводится к изменению этой структуры. Константа в уравнении (2.13) характеризует химическую активность реагентов [31] .

Еще одна фрактальная модель для определения предельной степени конверсии Q_пр в процессе синтеза полимеров, основанная на концепции дробного интегро-дифференцирования, предложена в работе [32]. По существу, эта модель представляет собой статический скейлинг. Она основана на предположении, что процесс синтеза полимеров представляет собой реакцию фрактальных объектов (макромолекулярных клубков) с размерностью D_f. Такую реакцию можно представить в виде «чертовой лестницы» [23].

Как отмечалось выше, такое же представление справедливо для реакции переэтерификации. Далее авторы [32] предложили, что предельная достигаемая в процессе синтеза полимеров степень конверсии Q_пр должна быть равна (1- ν_dp), поскольку остальная часть макромолекулярного клубка, характеризуемая ее долей ν_dp, в процессе эволюции (синтеза) участия не принимает. На рис. 2.9 приведено соотношение между Q_пр и (1 - ν_dp) для исследуемых реакций переэтерификации, которое демонстрирует примерное равенство этих параметров, подтверждающее сделанное выше предположение.

Отметим, что в случае макромолекулярных клубков реакция прекращается при D_f = 2,5 (в точке гелеобразования), тогда как в случае переэтерификации для низкомолекулярных молекул гептилбензоата уже при D_f = 2,0. Кроме того, Q_пр = 1,0 для синтеза полимеров достигается при D_f = 1,5 (протекаемый клубок [17]), а для переэтерификации – при D_f = 1,0. Это различие может быть обусловлено тем, что реакция переэтерификации останавливалась при t=300 мин и величины Q_пр, близкие к 1,0. не были получены, а статический скейлинг не дает зависимости от времени.

Как известно [13], константа скорости реакции k_d широко используется в кинетике химических реакций как показатель скорости их протекания. Наиболее простое уравнение, связывающее скорость реакции dQ/dt и степень конверсии Q с k_d, имеет вид [13]:

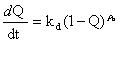,    (2.14)

где ρ_n-порядок реакции.

В случае ρ_n=1 (реакция первого порядка) величину k_d(k₁) легко получить из уравнения (2.14) (см. уравнение (2.7)). Однако ранее было показано [33], что понятие «константа скорости реакции» применимо только для реакций, протекающих во фрактальных средах. Для евклидовых пространств величина k_d является функцией продолжительности реакции, изменяясь по мере ее протекания. Именно такое изменение константы скорости первого порядка k₁ наблюдается в ходе модельной реакции переэтерификации при использовании слюды в качестве наполнителя-катализатора. Поэтому ниже будет дано теоретическое описание и объяснение причин изменения константы скорости переэтерификации как функции ее продолжительности t [34].

Кинетические кривые Q-t для четырех исследуемых реакции переэтэрификации приведены на рис. 2.10. Как можно видеть, все они оказались линейными, т.е., указанные реакции протекают в евклидовом пространстве [33, 35]. Скорость реакции dQ/dt можно записать следующим образом [35].

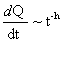,    (2.15)

где- h- показатель неоднородности (0<h<1), обращающихся в нуль для однородных (евклидовых) сред; при этом поведение является классическим dQ/dt= const.

Именно такое поведение предполагают линейные графики Q-t для реакции переэтерификации (рис. 2.10). Из уравнения (2.7)следует, что при dQ/dt= const величина (1-Q) должна изменяться по мере роста t, что в любом случае предполагает изменение k₁. Поэтому для рассматриваемых реакций вариацию k₁ со временем нельзя рассматривать как погрешность эксперимента и использовать в качестве константы скорости переэтерификации среднюю величину k₁ [34].

Взаимосвязь константы скорости переэтерификации k₁ и структуры молекулы гептилбензоата, характеризуемой размерностью D_f, дает уравнение (2.9). Отметим важный методологический аспект вывода этого уравнения. Константа 3 в показателе правой части соотношения (2.8) означает размерность евклидова пространства d_l, в котором протекает реакция, т.е., d=3. В случае изменения d₁ например, на d=2, уравнение (2.9) остается инвариантным к такой замене, по крайней мере, для регулярных фракталов, поскольку для последних величина D_f в пространстве d=2 меньше на единицу аналогичной размерности в случае d=3 [36].

На рис. 2.11÷2.13 приведено сравнение полученных экспериментально и рассчитанных согласно уравнению (2.9) величин k₁ как функции t при условии D_f = const. Как можно видеть, для реакций переэтерификации в присутствии НМС и СМК получено хорошее соответствие теории и эксперимента во всем интервале t, а для этой же реакции без слюды и в присутствии СМО – только при достаточно больших t (t>100 мин). Для двух последних случаев при малых временах (t<100 мин) расчет дал завышенные значения k₁. Это обстоятельство обусловлено не погрешностью метода, а невыполнением условия D_f = const для двух последних реакций переэтерификации.

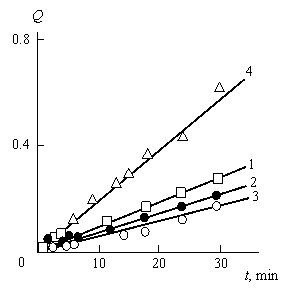
Рис. 2.10. Кинетические кривые Q-t для реакции переэтерификации без слюды (1) и в присутствии НМС (2), СМО (3), СМК (4). [34].

Рис. 2.11. Зависимость константы скорости переэтерификации k₁ от продолжительности реакции t. 1-экспериментальные данные ; 2,3 – расчет по уравнению (2.9) при D_f= const (2) и D_f = variant (3) [34].

Рис.2.12. Зависимости константы скорости переэтерификации k₁ в присутствии НМС от продолжительности реакции t. 1-экспериментальные данные; 2- расчет по уравнению (2.9) [34].

На это указывают очень низкие значения Q в интервале t = 0÷100 мин: для реакции без слюды и в присутствии СМО Q = 0,017÷0,050, тогда как для реакции в присутствии НМС и СМК эта же величина Q составляет 0,030÷0,123. Количественную оценку указанного эффекта можно выполнить следующим образом. Используя величину D_f =1.641 при t=300 мин для реакции переэтерификации без слюды, определим константу в соотношении (2.8), а затем рассчитаем величины D_fдля этой реакции в интервале t= 15÷60 мин с использованием указанной константы. Результаты такого расчета по уравнению (2.9) при D_f=variantпоказаны штриховой линией на рис. 2.11 и, как можно видеть, изменение D_f полностью объясняет примерное постоянство k₁ для указанной реакции.

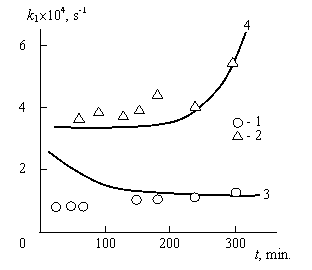
Рис. 2.13. Зависимости константы скорости переэтерификации k₁ в присутствии СМО (1,3) и СМК (2,4) от продолжительности реакции t. 1, 2-экспериментальные данные; 3, 4- расчет по уравнению (2.9)[34].

Сравнение данных рис. 2.11÷2.13 и приведенных выше величин D_f показало, что при D_f ≈1,64, примерно соответствующей размерности макромолекулярного клубка в хорошем растворителе (D_f≈1,67 [17], k₁=сonst даже для реакции, протекающей в евклидовом пространстве. При D_f <1,67 наблюдается рост k₁ по мере увеличения t, а при D_f > 1,67-снижение k₁ в аналогичных условиях. Следовательно, форма изменения функции k₁(t) определяется размерностью молекулы гептилбензоата [34].

Таким образом, изложенные выше результаты показали, что изменение константы скорости реакции переэтерификации со временем является характерным признаком протекания этой реакции в евклидовом пространстве. Теоретический расчет обнаружил хорошее соответствие с экспериментальными данными. Форма зависимости константы скорости реакции от времени (ее повышение или спад) определяется структурой продукта реакции (молекулы гептилбензоата).