
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.4 Фрактальный анализ каталитической активности слюды.
Композиционные полимерные материалы с улучшенными свойствами находят широкое применение в современной технике. Одним из наиболее прогрессивных направлений создания наполненных наноматериалов, где нанонаполнитель определяет кинетику синтеза, структуру и свойства конечного продукта и одновременно выполняет роль катализатора, является синтез полимеров в присутствии неорганических нанонаполнителей [1-3, 10].
Насыщенные сложные полиэфиры, в частности, полибутилентерефтолат (ПБТ), используют в качестве конструкционных термопластов, обладающих хорошей тепло- и износостойкостью, прекрасной формуемостью. Эти свойства позволяют также применять их в качестве матричного материала для полимерных нанокомпозитов [37-39]. Одним из перспективных путей поиска эффективных наполнителей – катализаторов является кинетическое исследование модельной реакции переэтерификации в присутствии различных неорганических соединений. Выяснение на примере модельной системы круга наиболее эффективных наполнителей – катализаторов позволит использовать их для получения наполненного ПБТ и сравнить каталитическую активность наполнителя и традиционных катализаторов (см. Приложение) [40].
Процесс катализа отражает сложную взаимосвязь между химическими и геометрическими параметрами поверхности [41]. Поэтому в настоящем разделе будут рассмотрены особенности использования слюды (как исходной, так и модифицированной) в качестве катализатора модельной реакции переэтерификации с точки зрения как химических, так и физических аспектов проблемы.
Наиболее просто микроскопическую модель процесса катализа можно представить следующими реакциями [42]:
А+S → Аа , (2.16)
В+ S → Ва , (2.17)
![]() , (2.18)
, (2.18)
D+S → Da , (2.19)
Е+S→ Еa , (2.20)
![]() , (2.21)
, (2.21)
где в рассматриваемом случае индекс «а» означает адсорбцию реагента на поверхности катализатора, реакция (2.18) является основной и имеет первый, порядок, реакция (2.21) – побочной и имеет второй порядок. Для рассматриваемой модельной реакции переэтерификации (2.18) и (2.21) можно соответственно записать так [40]:
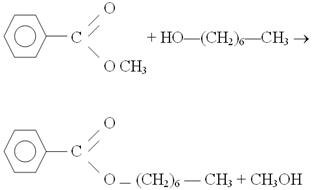 (2.22)
(2.22)
и
СН3-ОН+НО-(СН2)6-СН3 → СН3-О-(СН2)6-СН3+Н2О, (2.23)
где в реакции (2.22) формируется гептилбензоат и метанол, а в побочной реакции (2.23) – метиловый эфир и вода. Тогда селективность катализатора Sопределяется как отношение F/Cили отношение степени конверсии гептилбензоата и метилового эфира. Далее величину S можно определить из следующего уравнения [42]:
![]() , (2.24)
, (2.24)
где ![]() -скорость поступления на катализатор реагентов А и В (метилбензоата и гептанола-1), N-общее число мест поверхности катализатора, k1- константа скорости первого порядка (реакций (2.18) или (2.22)).
-скорость поступления на катализатор реагентов А и В (метилбензоата и гептанола-1), N-общее число мест поверхности катализатора, k1- константа скорости первого порядка (реакций (2.18) или (2.22)).
Поскольку побочная реакция (2.212) или (2.23) второго порядка выражена слабо, то селективность катализатора S в первом приближении можно определить так [40]:
![]() , (2.25)
, (2.25)
где – Q1- степень конверсии реакции первого порядка, в дальнейшем обозначаемая как Q.
Поскольку реакция переэтерификации протекает с интенсивным перемешиванием, обусловленным как пропусканием инертного газа через реакционную смесь, так и механическим перемешиванием, то полагаем ![]() ≈ const и далее можно записать [40]:
≈ const и далее можно записать [40]:
![]() . (2.26)
. (2.26)
На рис. 2.14 приведена зависимость N(t), где N дано в относительных единицах. Для модельной реакции переэтерификации в присутствии НМС, СМО и СМК. Поскольку предполагается, что после протекания реакции переэтерификации ее продукты (в основном гептилбензоат) удаляются с поверхности слюды в раствор, то расчет N проводили по отдельным временным интервалам. Этот аспект особенно важен в том случае, когда ![]() является функцией продолжительности переэтерификации, что наблюдалось для исследуемых реакций (см. рис. 2.11÷2.13). Как следует из данных рис. 2.14 при t<120 мин наблюдается нестационарный режим, характеризуемый ростом N по мере увеличения t, а при t>120 мин зависимости N(t) достигают асимптотических значений. Это означает, что в процессе катализа достигается динамическое равновесие поступающих на поверхность катализатора (слюды) молекул реагентов (метилбензоата и гептанола-1) и удаляемых с поверхности молекул продукта реакции (гептилбензоата). Общее число мест поверхности катализатора N располагается в таком порядке:
является функцией продолжительности переэтерификации, что наблюдалось для исследуемых реакций (см. рис. 2.11÷2.13). Как следует из данных рис. 2.14 при t<120 мин наблюдается нестационарный режим, характеризуемый ростом N по мере увеличения t, а при t>120 мин зависимости N(t) достигают асимптотических значений. Это означает, что в процессе катализа достигается динамическое равновесие поступающих на поверхность катализатора (слюды) молекул реагентов (метилбензоата и гептанола-1) и удаляемых с поверхности молекул продукта реакции (гептилбензоата). Общее число мест поверхности катализатора N располагается в таком порядке:
СМО>НМС>СМК.
Отметим, что величина N не определяет скорость реакции переэтерификации. На рис. 2.10 показаны кинетические кривые Q(t), из которых следует, что скорость реакции ведет себя диаметрально противоположно поведению N. Тем не менее. Определенное влияние величины N на ход реакции переэтерификации прослеживается. Как известно [43], кинетику реакции А+В→ инертный продукт, подобный (2.18), можно описать следующим образом:
ρА ~ t –D/4 (2.27)
где ρА-число «выживших» в ходе реакции частиц, D-размерность, контролирующая протекание реакции.
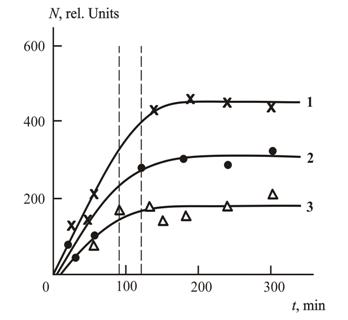
Рис.2.14. Зависимости общего числа мест на поверхности слюдыN от продолжительности t реакции переэтерификации в присутствии СМО (1), НМС (2) и СМК (3). Вертикальные штриховые линии указывают временной интервал изменения связности реакционной среды[40].
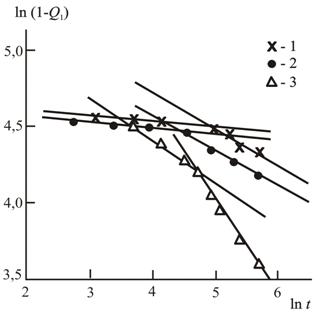
Рис. 2.15. Зависимости (1-Q) от t в двоичных логарифмических координатах, соответствующие соотношению (2.27) для реакции переэтерификации в присутствии СМО (1), НМС (2) и СМК (3) [40].
В случае протекания реакции в евклидовых пространствах величина D равна размерности этого пространства d, а для фрактальных пространств Dпринимается равной спектральной размерности ds [43]. На рис. 2.15 приведены зависимости ρА, где ρА определенно как (1-Q) от t в двоичных логарифмических координатах, соответствующие соотношению (2.27). Из графиков этого рисунка следует, что в интервале t= 90÷120 мин наблюдается изменение наклона линейных графиков для всех трех исследуемых реакций. Это изменение означает существенное увеличение степени реакционной среды, характеризуемой размерностью ds, и соответствующее ускорение реакции переэтерификации. На рис. 2.14 указанный временной интервал отмечен штриховыми линиями, показывающими, что изменение связности реакционной среды соответствует переходу к стационарному режиму функции N(t).
Как отмечалось выше, данные рентгенофотоэлектронной спектроскопии показали увеличение концентрации ионов металлов (Аl и Мg) на поверхности НМС и СМО в отличие от СМК. На рис. 2.16 приведены зависимости N от поверхностной концентрации как магния, С Мg, так и суммы концентраций магния и алюминия СМе в атомных %. Как можно видеть, в обоих случаях наблюдается рост N по мере увеличения концентрации металлов, причем характерно, что при некоторой ненулевой концентрации металлов величина N становится равной нулю, т.е., слюда перестает быть катализатором.
Каталитическую активность слюды можно оценить с помощью константы скорости катализа второго порядка k2кт, определяемой по формуле (2.4). На рис. 2.17 приведена зависимость k2кт от N, которая оказалась линейной и проходящей через начало координат, т.е., как следовало ожидать, увеличение числа активных мест катализа N приводит к повышению скорости этого процесса.
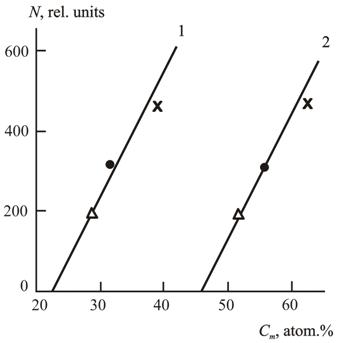
Рис.2.16. Зависимости общего числа мест на поверхности слюды N от поверхностной концентрации Мg (1) и (Мg+Аl) (2) для реакции переэтерификации. Обозначения те же, что и на рис. 2.15 [40].
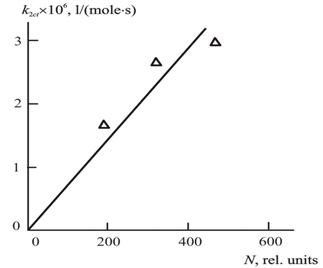
Рис.2.17. Зависимость константы скорости катализа второго порядка k2кт от общего числа мест на поверхности слюды N для реакции переэтерификации. [40].
Следовательно, изложенные выше результаты показали, что общее число активных мест на поверхности катализатора (слюды) как функция продолжительности реакции достигает своего стационарного значения только после некоторого временного промежутка, порядка 90÷120 мин. Прямой корреляции между общим числом мест на поверхности катализатора и степенью конверсии нет, но переход к стационарному режиму существенно изменяет степень связности реакционной среды. Между поверхностной концентрацией металлов, константой скорости катализа второго порядка и общим числом активных мест на поверхности катализатора обнаружены линейные корреляции.
Далее исследуем влияние структуры поверхности наполнителя-катализатора (слюды) на кинетику модельной реакции переэтерификации [44]. Для этой цели авторы [44] использовали скейлинговый подход [15].
Выше было показано, что если концентрация частиц и ловушек (захватов) велика или реакция происходит при интенсивном перемешивании, то процесс может рассматриваться как классическая реакция первого порядка и тогда закон спада концентрации частиц со временем с (t) описывается уравнением (2.10). Однако, если концентрация случайно расположенных ловушек мала, существуют области пространства (реакционной среды), практически свободные от ловушек, частицы, попавшие в эти области, могут достичь ловушек, лишь за весьма большое время и, следовательно, спад их числа со временем будет более медленным. Формальный анализ этой задачи показывает, что концентрация частиц спадает по закону [15]:
С(t) ≈ ехр (-Вtd/(d+2)), (2.28)
зависящему от размерности пространства d (В- константа).
Нужно отметить, что сингулярная зависимость от времени в уравнении (2.28) появляется одновременно с крупномасштабными флуктуациями (неоднородностью) плотности ловушек. Если ловушки могут двигаться, то их движение как бы усредняет влияние пространственной неоднородности, так что предположения, приводящие к выражению (2.10), будут выполняться лучше. Было показано, что в этом случае концентрация частиц спадает по комбинированному закону [15]:
С(t) ~ ехр (-Аt) ехр (-Вtd/(d+2)), (2.29)
где А пропорционально коэффициенту диффузии ловушек.
Поскольку, как отмечалось выше, реакция переэтерификации протекает с интенсивным перемешиванием, обусловленным как пропусканием инертного газа через реакционную среду, так и механическим перемешиванием (реакция «мусорщика» [45]), то для теоретического описания спада концентрации реагентов С(t) (как и ранее, С(t)=1-Q) со временем t использовано соотношение(2.29). На рис. 2.18÷2.20 показано совмещение теории и эксперимента для реакций переэтерификации без слюды (рис. 2.18), в присутствии НМС (рис 2.19) и СМК (рис. 2.20). Данные для СМО аналогичны приведенным на рис. 2.19 результатам и потому не показаны. Использованы две размерности пространства d, в котором протекает реакция: d=2 и d=3. как можно видеть, реакция переэтерификации без слюды примерно одинаково описывается двумя случаями. Но лучшее соответствие достигнуто при использовании d=3. Для реакции в присутствии НМС (и СМО) наблюдается переход, пространства от d=3 к d=2, т.е., такой переход предполагает протекание реакции переэтерификации на плоской поверхности (размерность поверхности слюды dn=2 [46]) наполнителя-катализатора. И, наконец, в случае СМК размерность пространства вновь становится d=3.
Рассмотрим физические основы указанных измерений размерности и, следовательно, типа пространства, в котором протекает рассматриваемая реакция.

Рис. 2.18. Зависимости (1-Q) от t, соответствующие соотношению (2.29), для реакции переэтерификации без слюды при d=2 (1) и d=3 (3). Сплошная линия – экспериментальные данные [44].

Рис. 2.19. Зависимости (1-Q) от t, соответствующие соотношению (2.29), для реакции переэтерификации в присутствии НМС. Обозначения те же, что и на рис.2.18[44].

Рис.2.20. Зависимости (1-Q) от t, соответствующие соотношению (2.29), для реакции переэтерификации в присутствии СМК. Обозначения те же, что и на рис.2.18[44].
оценить величину dn для трех применяемых типов слюды можно помощью соотношения [5]:
k2кт ~ t(1- dn)/2, (2.30)
где-К2к- константа скорости катализа второго порядка, рассчитанная согласно уравнению (2.4). Константу пропорциональности в соотношении (2.30) можно определить при условии dn=2,0 для НМС [46].
В табл. 2.4. приведены константы соотношения (2.29), при использовании которых получено наилучшее соответствие с экспериментом (А, В и d), а также оцененные согласно (2.30) величины dn. Как можно видеть, обработка слюды гидроксидом натрия практически не изменяет величину dn для СМО по сравнению с исходной слюдой НМС, тогда как обработка серной кислотой приводит к тому, что поверхность СМК становится фрактальным объектом с размерностью dn=2,23. Если значения dn для НМС и СМО характеризуют по существу евклидову поверхность и, как следствие, рассматриваются в d=2, то для СМК фрактальная поверхность с dn >2 может рассматриваться только в евклидовом пространстве с dn =3, что и наблюдается согласно данным рис 2.20 и табл. 2.4. Увеличение dn для СМК по сравнению с аналогичной величиной для НМС и СМО полностью согласуется с повышением удельной поверхности Su для первой (Su ≈21,3 и 18,4 мг/2, соответственно [10]).
Таблица 2.4.
Характеристики наполнителя-катализатора (слюды), применяемого в модельной реакции переэтерификации [44].
Слюда | d | А х 104 | В х 103 | dn | vэф,отн. ед. |
| Нет | 3 | 5,2 | 5,0 | - | 8 |
| НМС | 2 | 5,2 | 4,0 | 2,0 | 2 |
| СМО | 2 | 4,8 | 3,9 | 1,964 | 2 |
| СМК | 3 | 10,0 | 10,0 | 1,230 | 8 |
Изменение размерности пространства приводит к вариации эффективного объема реакционной среды vэф, в котором может протекать реакция. Величина vэф определяется так [47]:
Vэф = Ldэфε3-dэф, (2.31)
где L- верхний предел фрактального поведения, ε-масштаб измерения, dэф-эффективная размерность среды.
Оценка Vэф согласно уравнению (2.31) при произвольных значениях L=2 и ε=0,5, а также условии dэф= dп показала существенное различие эффективного объема для рассматриваемых реакций (табл. 2.4).
Как отмечалось выше, константа А в соотношении (2.29) пропорциональна коэффициенту диффузии ловушек [15,45]. Следует ожидать, что увеличение и Vэф , и А (коэффициента диффузии ловушек) приведет к росту степени конверсии Q реакции переэтерификации. На рис. 2.21 показана зависимость величины Q при t= 300 мин. от произведения АVэф (в относительных единицах) для исследуемых реакций, подтверждающая это предположение. Указанная зависимость линейна, т.е., факторы А и Vэф имеют одинаковую степень влияния на величину Q и проходит через начало координат, т.е., наблюдается очевидное условие: при А=0 или Vэф=0 Q=0.
Изложенные выше результаты позволяют объяснить кинетику модельной реакции переэтерификации. На рис. 2.10 приведены кинетические кривые Q-t для четырех исследуемых реакций. Все они оказались прямолинейными, т.е., как показано выше, реакция переэтерификации протекает в евклидовом пространстве с размерностью d=2 или d=3 (см. табл. 2.4). Реакция без слюды занимает промежуточное положение из-за более высокой размерности d, но относительно небольшого коэффициента диффузии. Введение в реакционную среду НМС и СМО приводит к снижению и d, и А, что уменьшает интенсивность реакции. И наконец, для реакции переэтерификации в присутствии СМК получены наибольшие значения и d (d=3), и А (коэффициента диффузии), в силу чего эта реакция протекает гораздо быстрее остальных. Отметим также, что коэффициент В в соотношении (2.29) пропорционален числу реакционноспособных мест реагентов [45] и его величина наибольшая для реакции переэтерификации в присутствии СМК (табл. 2.4).
Следовательно, изложенные выше результаты показали применимость скейлингового подхода в форме соотношения (2.29) для анализа каталитической активности слюды в модельной реакции переэтерификации. Изменение размерности пространства, в котором протекает реакция, существенно влияет на ее интенсивность. Для повышения скорости реакции требуется увеличение как размерности евклидова пространства, так и коэффициента диффузии реагентов [44].

Рис.2.21. Зависимость степени конверсии Q при t=300 мин. от произведения АVэф для реакций переэтерификации[44].
Как было показано выше поверхность НМС и СМО представляет собой евклидов объект сdn≈2,0, тогда как поверхность СМК фрактальна (dn=2,23). Поэтому возникает вопрос о степени доступности поверхности слюды для реализации катализа. В такой трактовке определяющее значение имеет не общее число активных мест поверхности катализатора N, а число доступных мест Nдост, определяемое следующим соотношением [48]:
Nдост ~ Ldu, (2.32)
где L-характеристический размер пластины слюды, du-фрактальная размерность неэкранированной (доступной) поверхности, определяемая, в свою очередь, из уравнения [48]:
![]() (2.33)
(2.33)
где d – размерность евклидова пространства, в котором рассматривается фрактальный объект (очевидно, в нашем случае d=3), dw размерность траектории случайного блуждания частиц (реагентов). Поскольку для реакции переэтерификации кинетика описывается линейными зависимостями Q-t(рис. 2.10), то это означает протекание реакций в евклидовом пространстве и тогда dw=2 [49].
В качестве величины L был выбран линейный размер пластины слюды (230 нм, [10]), а в качестве структурной характеристики поверхности наполнителя-катализатора - отношение (Nдост/N), определяющее долю активных мест поверхности слюды, способных к реализации катализа. Было обнаружено, что между величиной Q при максимальном значении t=300 мин и (Nдост /N) наблюдается линейная корреляция, что позволило нормировку указанного отношения из условия: (Nдост /N)=1 при Q=1 (напомним, что и Nдост, N определены в относительных единицах). На рис. 2.22 и 2.23 приведены зависимости основных характеристик реакции переэтерификации Q и k1 (при t=300 мин) от нормированного отношения (Nдост /N)н.Как можно видеть, обе указанные корреляции линейны, и проходят через начало координат, т.е., структура поверхности наполнителя-катализатора контролирует процесс переэтерификации.
Далее рассмотрим вопрос взаимосвязи структур поверхности слюды, характеризуемой отношением (Nдост /N)н и продукта реакции (молекулы гептилбензоата), характеризуемой размерностью Df. На рис. 2.24 приведена зависимость Df (Nдост /N)н, которая имеет примечательный вид. Как можно видеть, наблюдается линейный спад Df. по мере увеличения (Nдост /N)н. По существу это означает, что увеличение числа мест взаимодействия поверхности слюды и молекулы гептилбензоата или составляющих ее частей (см. рис.2.22) приводит к все большей степени «растяжки» указанной молекулы на поверхности катализатора [29] и, как следствие, к снижению Df. При экстрополяции графика рис. 2.24 с (Nдост /N)н=0 получим Df=2,0, т.е., в этом случае молекула гептилбензоата эквивалентна полимерной макромолекуле в идеальном Θ-растворителе [17]. При (Nдост /N)н=1 величина Df≈1,14, т.е., близка к размерности полностью вытянутой (стержне подобной)
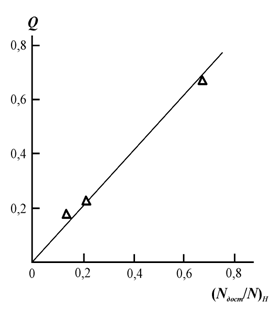
Рис.2.22. Зависимость степени конверсии Q, при t=300 мин от относительной доли доступных для катализа мест поверхности слюды (Nдост /N)н в случае реакции переэтерификации [50].
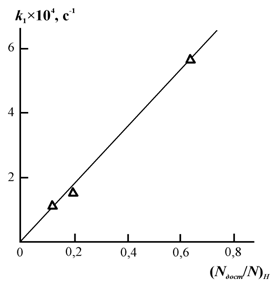
Рис.2.23. Зависимость константы скорости первого порядка k1 от относительной доли доступных для катализа мест поверхности слюды (Nдост/N)н в случае реакции переэтерификации[50].
молекулы, для которой Df=1,0 [17], но не достигает этой величины, вероятно, из-за жесткости валентных связей молекулы гептилбензоата.
Указанное изменение размерности фракталоподобной молекулы гептилбензоата или составляющих ее частей (метилбензоата и гептанола-1) приводит к увеличению числа реакционноспособных (доступных для протекания переэтерификации) активных мест Nu указанной молекулы согласно соотношению (2.32). Как показано выше, в рамках скейлингового подхода реакцию переэтерификации можно описать теоретической моделью реакции «мусорщика» [45]. В этом случае спад концентрации реагентов описывается скейлинговым соотношением (2.29), где В-константа, пропорциональная числу реакционноспособных мест в системе. На рис. 2.25 приведено соотношение между В и Nu, т.е., числом реакционноспособных мест, оцененных двумя разными способами: согласно уравнениям (2.29) и (2.32), соответственно. Как можно видеть, между указанными параметрами наблюдается линейная корреляция, проходящая через начало координат. Это означает, что величина В полностью определяется структурой молекулы гептилбензоата или ее, составляющих частей. Характеризуемой размерностью Df, которая, в свою очередь, контролируется структурой поверхности наполнителя – катализатора (слюды).
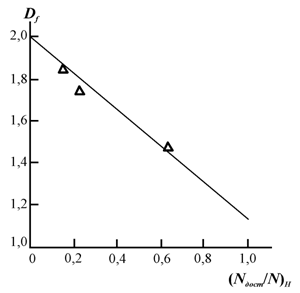
Рис.2.24. Зависимость размерности молекулы гептилбензоата Df от относительной доли доступных для катализа мест поверхности слюды (Nдост /N)н в случае реакции переэтерификации[50].
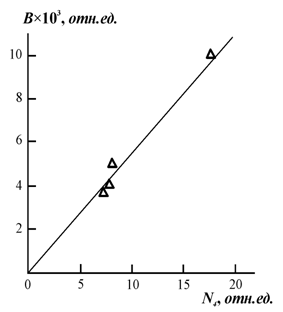
Рис.2.25.Соотношение числа реакционноспособных мест системы В и молекулы гептилбензоата Nu в случае реакции переэтерификации[50].
Следовательно, изложенные выше данные показали, что структуру поверхности наполнителя-катализатора (в рассматриваемом случае – слюды) можно описать относительным числом доступных для катализа активных мест поверхности. Этот фактор контролирует как основные характеристики модельной реакции переэтерификации, так и структуру продукта реакции (молекулы гептилбензоата).
