
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.2. Особенности кинетики модельной реакции переэтерификации, катализируемой наночастицами соединений металлов
Выше было показано очень сильное влияние наночастиц неорганических соединений металлов на процесс модельной реакции переэтерификации, как количественное, так и качественное. Количественно это влияние выражается в существенном изменении константы скорости реакции первого порядка k1: от 8,91х10-4с-1 для реакции переэтерификации в присутствии СаО до 0,004х10-4с-1- в присутствии ВеО, т.е., более чем на три порядка [1]. Качественное различие заключается в типе кинетических кривых степень конверсии – продолжительность реакции Q(t): для реакции с большимиk1(>2,80х10-4с-1) они имеют автоускоренный характер, а для реакции с меньшими k1-автозамедленный. Авторы [13] выполнили аналитический вывод критерия перехода кривых Q(t) от автоускоренного к автозамедленному режиму.
На рис. 4.7 приведены кинетические кривые Q(t) для реакции переэтерификации без катализатора и в присутствии неорганических соединений металлов ВеО, Fe2O3, CeO2 и BaO. Как можно видеть, реакция без катализатора имеет примерно линейную кинетику, реакция в присутствии ВеО иFe2O3 - автозамедленную и в присутствии CeO2 и BaO-автоускоренную, причем кинетическая кривая Q(t) для реакции без катализатора представляет собой границу, разделяющую указанные два режима.
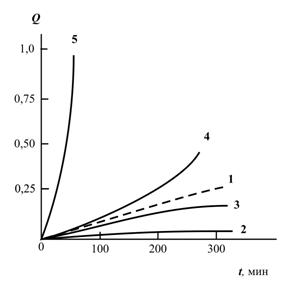
Рис.4.7. Кинетические кривые степень конверсии-продолжительность реакции Q(t) для реакции переэтерификации без наполнителя (1) и в присутствии ВеО(2), Fe2O3(3), CeO2(4), BaO(5) [13].
В работах [14,15] было показано, что причиной перехода от автозамедленного кинетического режима термоокислительной деструкции полимеров к автоускоренному является структурный фактор, а именно, повышение фрактальной размерности макромолекулярного клубка в расплаве. Есть все основания полагать, что этот же фактор будет определяющим и в рассматриваемом случае. Фрактальную размерность Dfфракталоподобной молекулы гептилбензоата можно определить с помощью уравнения (2.9). В табл.4.2 приведены величины k1 по данным работы [1], рассчитанные согласно уравнению (2.9) значения Df и тип кривой Q(t) для реакции переэтерификации с участием 16 указанных неорганических соединений металлов, а также для этой же реакции без катализатора. Из данных табл. 4.2 следует достаточно ясно выраженная тенденция: для невысоких Df, примерно <1,80, наблюдаются большие значения k1 и автоускоренная кинетика, а для Df >1,80-малые значения k1 и автозамедленная кинетика реакции переэтерификации. Это позволяет сделать вывод о структурном происхождении изменения кинетического режима реакции переэтерификации. В случае невысоких Df фракталоподобные молекулы гептилбензоата и его компонентов менее компактны и реакция может протекать во внутренних областях их структуры. При повышении Df указанные молекулы компактизируются и реакция протекает только на их поверхности. Это допущение положено в основу аналитического вывода критерия изменения кинетического режима, а точнее, определения критического значения Df (![]() ), при котором реализуется указанный переход. Далее, по аналогии с работами [14,15] авторы [13] предположили, что наблюдаемое изменение типа кинетической кривой Q(t) происходит в том случае, когда число реакционно-способных мест молекулы на ее поверхности Nпов и в ее объеме Nоб становится равным [13]:
), при котором реализуется указанный переход. Далее, по аналогии с работами [14,15] авторы [13] предположили, что наблюдаемое изменение типа кинетической кривой Q(t) происходит в том случае, когда число реакционно-способных мест молекулы на ее поверхности Nпов и в ее объеме Nоб становится равным [13]:
Nпов= Nоб (4.8).
Рассмотрим способы оценки параметров в критерии (4.8). Основным структурным элементом в растворе является молекула гептилбензоата, которая представляет собой фракталоподобный объект. Это означает, что реакция в ее объеме протекает не в евклидовом, а во фрактальном пространстве. Напомним (см. также главу 2), что в таком пространстве реакцию переэтерификации схематически можно представить в виде «чертовой лестницы» [16,17]. Ее горизонтальные отрезки соответствуют временным интервалам, где реакция не идет. В этом случае реакция описывается с использованием фрактального времени, которое принадлежит точкам Канторова множества [17]. Если же реакция протекает в евклидовом пространстве, то время принадлежит множеству действительных чисел.
Для описания эволюционных процессов с фрактальным временем используется математический аппарат дробного дифференцирования и интегрирования [18] или как показано в главе 2, эквивалентные методы концепции странной (аномальной) диффузии [19]. Как показано в работе [20], в этом случае дробный показатель νдр совпадает с фрактальной размерностью Кантора и указывает на долю состояний системы, сохраняющихся за все время эволюции. Напомним, что множество Контора рассматривается в одномерном евклидовом пространстве с размерностью d=1 и поэтому его фрактальная размерность df <1 в силу определения фрактала [17]. Для фрактальных объектов евклидовых пространств с более высокими размерностями (d>1) в качестве νдр следует принимать дробную часть df (в нашем случае - Df) или [15]:
νдр= Df - (d-1). (4.9)
Таблица 4.2.
Характеристики кинетики модельной реакции переэтерификации в присутствии 30 мас.% неорганических соединений металлов [13].
| Соединение металла | k1х10-4с-1[220] | Df | Тип кинетической кривой Q(t) |
| - | 0,18±0,02 | 1,85 | линейный |
| CaO | 8,91±0,52 | 1,54 | автоускоренный |
| РbО | 5,38±0,33 | 1,54 | автоускоренный |
| ВаО | 4,40±0,21 | 1,62 | автоускоренный |
| ZnО | 3,63±0,20 | 1,67 | автоускоренный |
| СоО | 2,80±0,20 | 1,70 | автоускоренный |
| MgO | 1,96±0,14 | 1,66 | линейный |
| MoS2 | 1,85±0,11 | 1,58 | линейный |
| CuO | 0,26±0,02 | 1,81 | автозамедленный |
| Al2 O3 | 0,25±0,04 | 2,03 | автозамедленный |
| CeO2 | 0,20±0,01 | 1,78 | автоускоренный |
| La2O3 | 0,19±0,01 | 1,80 | автозамедленный |
| ZnS | 0,16±0,01 | 1,86 | автозамедленный |
| Fe2O3 | 0,13±0,01 | 1,95 | автозамедленный |
| TiO2 | 0,11±0,008 | 2,10 | автозамедленный |
| ZrO2 | 0,08±0,004 | 2,06 | автозамедленный |
| BeO | 0,004±0,0002 | 2,29 | автозамедленный |
Тогда величина νдр характеризует долю реагирующих молекул, сохраняющуюся, т.е., не принимающую участия в процессе эволюции (реакции). Очевидно, доля молекулы β, способная к химическим превращениям в ходе реакции, определяется так [14]:
b = 1- νдр = 1- [ Df - (d -1)] = d - Df. (4.10)
Следовательно, реальную величину числа реакционно-способных мест Nоб в объеме молекулы можно записать следующим образом [13]:
Nоб= Nм(d- Df)- Nпов, (4.11)
где Nм-число реакционно-способных мест на молекулу при условии их полной доступности, Очевидно, величина Nм определяется химическим строением реагента.
Соотношение параметров Nоб и Nпов контролируется соотношением объема Vфр и поверхности Sфр фракталоподобного объекта, которое равно [21]:
![]() , (4.12)
, (4.12)
где R-радиус фракталоподобного объекта, в нашем случае равный радиусу инерции Rq молекулы гептилбензоата.
Точно оценить последний параметр достаточно затруднительно. Поэтому в работе [13] использована формула для оценки Rq в случае поликарбоната [22]:
![]() (4.13)
(4.13)
где Mw – средневесовая молекулярная масса молекулы гептилбензоата, с заменой показателя 0,5 на величину 0,65, типичную для хорошего растворителя [22]. Для молекулы гептилбензоата Mw=215, что дает Rq=32,4? согласно уравнению (4.13). Поскольку указанная оценка имеет приближенный характер, то далее будет использована величина Rq=3 нм [13].
Сочетание уравнений (4.8)-(4.13) позволяет получить структурный критерий перехода кинетических кривых Q(t) от автозамедленного режима к автоускоренному и наоборот [13]:
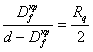 , (4.14)
, (4.14)
где - ![]() -критическое значение Df при указанном переходе, а величина Rq дается в нм.
-критическое значение Df при указанном переходе, а величина Rq дается в нм.
Отметим ряд важных особенностей уравнения (4.14). Во-первых, в этом уравнении отсутствует параметр Nм, т.е., величина ![]() не зависит от химического строения полимера. Во-вторых, увеличение Rq приводит к повышению
не зависит от химического строения полимера. Во-вторых, увеличение Rq приводит к повышению ![]() . Это полностью согласуется с предположением, послужившим основой для вывода уравнения (4.14). Величина Nоб растет пропорционально кубу Rq, а Nпов – квадрату Rq, т.е., увеличение Rq приводит к повышению отношения Vфр/Sфр. В третьих, уравнение (4.14) объясняет отсутствие авто ускоренного режима для большинства реакций синтеза полимеров: в этих реакциях быстрый рост Rq в отличие от модельной реакции переэтерификации, где Rq=const, повышает величину
. Это полностью согласуется с предположением, послужившим основой для вывода уравнения (4.14). Величина Nоб растет пропорционально кубу Rq, а Nпов – квадрату Rq, т.е., увеличение Rq приводит к повышению отношения Vфр/Sфр. В третьих, уравнение (4.14) объясняет отсутствие авто ускоренного режима для большинства реакций синтеза полимеров: в этих реакциях быстрый рост Rq в отличие от модельной реакции переэтерификации, где Rq=const, повышает величину ![]() . Так, уже при Rq=5нм
. Так, уже при Rq=5нм ![]() =2,14, т.е., равна фрактальной размерности макромолекулярного клубка, при которой реакция синтеза полимеров практически прекращается [23]. При типичных размерах макромолекулярного клубка в конце синтеза порядка Rq=25 нм
=2,14, т.е., равна фрактальной размерности макромолекулярного клубка, при которой реакция синтеза полимеров практически прекращается [23]. При типичных размерах макромолекулярного клубка в конце синтеза порядка Rq=25 нм ![]() =2,78, т.е., выше размерности этого же клубка в процессе гелеобразования, где Df ≈2,5 [24,25]. В четвертых, автоускорение реакции радикальной полимеризации очень четко просматривается на ее начальном участке из-за резкого снижения Df [26,27] и, следовательно, достижения условия Df <
=2,78, т.е., выше размерности этого же клубка в процессе гелеобразования, где Df ≈2,5 [24,25]. В четвертых, автоускорение реакции радикальной полимеризации очень четко просматривается на ее начальном участке из-за резкого снижения Df [26,27] и, следовательно, достижения условия Df <![]() .
.
Рассмотрим граничные условия для уравнения (4.14). Для Df=0, т.е., для точечного объекта, Rq=0 и критерий (4.14) определив для нуль- мерного объекта. Для Df=3 Rq→∞ и, как и следовало ожидать для евклидова объекта, масштаб измерения не играет роли.
На рис. 4.8 приведена зависимость k1 от Df в логарифмических координатах. Как и ожидалось, наблюдается линейное снижение lnk1 по мере ростаDf.. Полученное согласно уравнению (4.14) критическое значение Df указано на рис. 4.8 вертикальной штриховой линией. Как можно видеть, оно действительно служит границей для автоускоренной и автозамедленной кинетики реакции переэтерификации.
Авторы [13] выполнили также оценку глубины взаимопроникновения l молекул метилбензоата и гептанола- l для реакций в присутствии СаО (Df=1,54) и ВеО (Df=2,29). Величину l можно оценить согласно уравнению [28]:
![]() , (4.15)
, (4.15)
где а - нижний линейный масштаб фрактального поведения молекулы, d-размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d=3).
Полагая, а=3?, Мw=110 для указанных выше молекул и оценив величину Rq для них как 21? согласно уравнению (4.13), получим ![]() =10? для молекулы с Df=1,54 (СаО) и
=10? для молекулы с Df=1,54 (СаО) и ![]() =3,7? для молекулы с Df=2,29 (ВеО). Иначе говоря, если в первом случае молекулы почти полностью проникают друг в друга (2
=3,7? для молекулы с Df=2,29 (ВеО). Иначе говоря, если в первом случае молекулы почти полностью проникают друг в друга (2![]() ≈Rq), то во втором они могут реагировать только в поверхностном слое толщиной 3,7 ?, т.е., примерно 18% от Rq.
≈Rq), то во втором они могут реагировать только в поверхностном слое толщиной 3,7 ?, т.е., примерно 18% от Rq.
Следовательно, изложенные выше результаты наглядно продемонстрировали, что переход кинетических кривых реакции переэтерификации от автозамедленного к автоускоренному режиму определяется структурным фактором, а именно, достижением фракталоподобной молекулой (продукта реакции) критического значения фрактальной размерности, при котором число реакционноспособных мест в объеме и на поверхности молекулы становятся равны. В рамках фрактального анализа получено аналитическое соотношение, подтверждающее эту гипотезу.
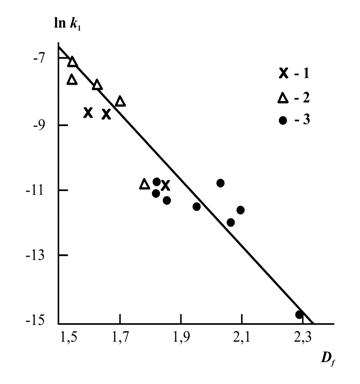
Рис.4.8. Зависимость константы скорости первого порядка k1 от фрактальной размерности продукта реакции Df для реакции переэтерификации в логарифмических координатах. Тип кинетических кривыхQ(t): 1- линейный, 2- автоускоренный, 3- автозамедленный. Вертикальная штриховая линия указывает величину ![]() [13].
[13].
В работе [29] эффект автоускорения в кинетике модельной реакции переэтерификации в присутствии ряда наночастиц оксидов металлов был исследован в рамках фрактальной кинетики химических реакций [30-32]. Как известно [31], среднее число мест кластера <S>, посещаемых случайным блужданием, которым моделируются молекулы метилбензоата и гептанола-1, зависит от времени tследующим образом:
![]() , (4.16)
, (4.16)
где ![]() -эффективная спектральная размерность реакционной среды, в которой диффундируют случайные блуждания. Величина
-эффективная спектральная размерность реакционной среды, в которой диффундируют случайные блуждания. Величина ![]() связана с показателем неоднородности реакционной среды h(0<h≤1) уравнением (3.8). При h=0 система (реакционная среда) становится однородной (евклидовой), а при h>0 она является гетерогенной (фрактальной).
связана с показателем неоднородности реакционной среды h(0<h≤1) уравнением (3.8). При h=0 система (реакционная среда) становится однородной (евклидовой), а при h>0 она является гетерогенной (фрактальной).
На рис. 4.9 приведены экспериментальные кинетические кривые Q(t) (точки) для реакции переэтерификации, катализируемой тремя оксидами металлов (СаО, ВеО и ZnO). Как можно видеть, эти кривые Q(t) имеют приблизительно квадратичную форму, что позволяет записать соотношение (4.16) в виде [29]:
Q ~ tds¢. (4.17)
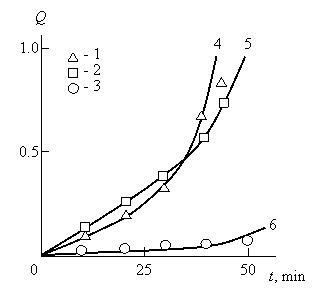
Рис.4.9. Экспериментальные (1-3) и рассчитанные по уравнению (4.18) (4-6) кинетические кривые Q(t) для реакции переэтерификации, катализируе-мой наночастицами СаО (1,4), ВаО(2,5) и ZnO(3,6) [29].
На рис. 4.10 приведены зависимости Q(t) в двойных логарифмических координатах для реакции переэтерификации, катализируемой наночастицами СаО и ВаО, которые соответствуют соотношению (4.17). Как можно видеть, в обоих случаях получены линейные зависимости, распадающиеся на два участка. При малых временах (t≤27 мин) величина ![]() , определенная по наклону этих линейных участков, равна 1,1 и, согласно уравнению (3.8) получим h=0,45. Таким образом, при малых временах реакция переэтерификации протекает в неоднородной среде с небольшими значениями
, определенная по наклону этих линейных участков, равна 1,1 и, согласно уравнению (3.8) получим h=0,45. Таким образом, при малых временах реакция переэтерификации протекает в неоднородной среде с небольшими значениями ![]() , что определяет ее относительно небольшую скорость (см. рис. 4.9). При относительно больших временах (t>27 мин) скорость реакции существенно возрастает и из наклона линейных графиков рис. 4.10 можно определить величину
, что определяет ее относительно небольшую скорость (см. рис. 4.9). При относительно больших временах (t>27 мин) скорость реакции существенно возрастает и из наклона линейных графиков рис. 4.10 можно определить величину ![]() для этого участка, равную 2. Согласно уравнению (3.8), это означает h=0, т.е., при t>27 мин. реакция переэтерификации протекает в однородной среде (евклидовом пространстве). Иначе говоря, при t=27 мин. наблюдается зависимый от времени переход реакции переэтерификации от неоднородной или гетерогенной (фрактальной) к однородной или гомогенной (евклидовой) кинетике. Указанный переход определяет резкое увеличение скорости реакции и соответствующий рост степени конверсии Q.
для этого участка, равную 2. Согласно уравнению (3.8), это означает h=0, т.е., при t>27 мин. реакция переэтерификации протекает в однородной среде (евклидовом пространстве). Иначе говоря, при t=27 мин. наблюдается зависимый от времени переход реакции переэтерификации от неоднородной или гетерогенной (фрактальной) к однородной или гомогенной (евклидовой) кинетике. Указанный переход определяет резкое увеличение скорости реакции и соответствующий рост степени конверсии Q.
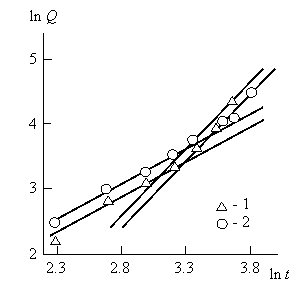
Рис.4.10. Зависимость степени конверсии Q от продолжительности реакции t в двойных логарифмических координатах для реакции переэтерификации, катализируе-мой наночастицами СаО(1) и ВаО(2) [29].
Следовательно, кривые Q(t) для рассматриваемой реакции переэтерификации можно моделировать следующим простым уравнением:
![]() , (4.18)
, (4.18)
где коэффициент с1 является функцией структуры молекул гептилбензоата, которую количественно можно охарактеризовать ее фрактальной размерностью Df, определяемой с помощью формулы (2.9).
Для рассматриваемых оксидов металлов увеличение Df от 1,54 для СаО до 1,81 для ZnO приводит к снижению с1 от 0,042 до 0,002, соответственно, т.е., примерно в 20 раз. Таким образом, участки кинетических кривых Q(t) при t≤27 мин. можно моделировать линейной корреляцией, а при t>27 мин.-квадратичной согласно уравнению (4.18). Результаты такого моделирования показаны на рис. 4.9 сплошными линиями. Как можно видеть, получено хорошее соответствие теории и эксперимента.
Отметим интересный аспект, вытекающий из указанного моделирования. Скорость реакции переэтерификации, которая различается для случаев катализа наночастицами СаО и ZnO, в рассматриваемом случае не зависит от связности реакционной среды, поскольку величина ![]() в трех приведенных примерах одинакова, а определяется структурой продукта реакции (молекулы гептилбензоата), т.е., величиной Df [29].
в трех приведенных примерах одинакова, а определяется структурой продукта реакции (молекулы гептилбензоата), т.е., величиной Df [29].
Порядок реакции n связан с показателем неоднородности h следующим образом [32]:
![]() . (4.19)
. (4.19)
Как следует из приведенных выше данных, при t≤27 мин. n=2,82, а при t>27 мин. реакция переэтерификации становится классической реакцией второго порядка.
Рассмотрим физические причины увеличения размерности ![]() по мере роста t. Как известно [33], величина <S> связано с числом шагов N (или временем t) частицы до контакта с кластером следующим соотношением:
по мере роста t. Как известно [33], величина <S> связано с числом шагов N (или временем t) частицы до контакта с кластером следующим соотношением:
![]() . (4.20)
. (4.20)
Очевидно, что по мере протекания реакции переэтерификации число реакционно-способных молекул метилбензоата и гептанола-1 уменьшается и им требуется сделать больше шагов (соотношение (4.20)) или затратить больше времени (соотношение (4.16)) для того, чтобы «найти» реакционно-способную молекулу – партнера для реализации реакции образования молекулы гептилбензоата. В свою очередь, в работе [30] показано, что увеличениеN (или t) приводит к росту ![]() , величина, которой, асимптотически стремится к соответствующему значению, для евклидова пространства. Это является физической основой наблюдаемого, зависимого от времени, перехода от фрактальной к евклидовой кинетике для модельной реакции переэтерификации [29].
, величина, которой, асимптотически стремится к соответствующему значению, для евклидова пространства. Это является физической основой наблюдаемого, зависимого от времени, перехода от фрактальной к евклидовой кинетике для модельной реакции переэтерификации [29].
Следовательно, изложенные выше результаты показали, что для реакции перэтерификации, катализируемой наночастицами неорганических соединений металлов, автоускоренный режим кинетики определяется зависимым от времени переходом от фрактального поведения к евклидову. Этот переход обусловлен повышением эффективной спектральной размерности реакционной среды из-за увеличения временного промежутка между столкновениями реагирующих молекул.
Постоянным предметом исследования в органической и неорганической химии является вопрос увеличения скорости химических реакций (например, синтеза полимеров), что позволяет снизить продолжительность их протекания и, следовательно, повысить производительность процесса. Для этой цели применяется достаточно много способов, например, повышение температуры реакции, катализ, интенсивное перемешивание реакционной среды и т.д. [34]. Однако все эти способы следует считать внешними факторами воздействия на скорость химических реакций. Гораздо меньше исследована проблема интенсификации внутренних факторов. В связи с этим следует отметить появление в последнее время ряда новых тенденций.
Одной из таких тенденций является синтез полимеров в присутствии разного рода наполнителей, которые одновременно служат катализатором реакции [1,35]. Второй тенденцией является исследование химических реакций в рамках физических подходов [36-40], из которых наибольшее применение получили фрактальный анализ [11]. В рамках последнего подхода в рассмотрение процесса синтеза введены такие основополагающие понятия как структура продуктов реакции, характеризуемая их фрактальной (хаусдорфовой), размерностью Df [41] и связность реакционной среды, характеризуемая спектральной (фрактальной) размерностью ds [42]. В свою очередь, процессы диффузии для фрактальных реакций (странные или аномальные) принципиально отличаются от протекающих в евклидовых пространствах и описываемых классическими законами диффузии [19] (см. подробнее раздел 2.5). Поэтому авторы [43] дали описание кинетики модельной реакции переэтерификации в присутствии 14 оксидов металлов в рамках концепции странной (аномальной) диффузии.
Авторы [19] сформировали дробное уравнение процессов переноса, а именно, формулу (2.39), где в зависимости от конкретного значения α различают персистентные (супердиффузионные, 1<α≤2) и антиперсистентные (субдиффузионные, 0<α≤1) процессы. В свою очередь, в работе [44], было получено уравнение, которое связывает величины α и Df, а именно, уравнение (2.45). В этом уравнении было принято β=const=0,25, где β – показатель в уравнении (2.39).
Как показано выше, кинетические кривые Q(t) для реакции переэтерификации в присутствии разных оксидов металлов различаются как качественно, так и количественно (рис. 4.7). Это позволило авторам [43] построить зависимость степени конверсии Q от активного времени tα для 14 исследуемых реакций переэтерификации в присутствии оксидов металлов (см. табл.4.2) и аналогичной реакции без наполнителя- катализатора для t=50 мин. Как можно видеть, эта зависимость хорошо аппроксимируется линейной корреляцией, аналитически описываемой так [43]:
![]() . (4.21)
. (4.21)
На рис. 4.11 также приведена зависимость Q(ta) для реакции переэтерификации в присутствии слюды с разной обработкой поверхности, которая описывается эмпирическим соотношением (2.42). Характерно, что соотношение (4.21) лучше описывает кинетические кривые с автоускорением, а соотношение (2.42) –линейные автозамедленные кинетические кривые. Таким образом, тип кинетической кривой также сказывается на величине Q: для одной и той же величины активного времени tα величина Q примерно на 22% выше для автоускоренной кинетики, чем для линейной автозамедленной [43].
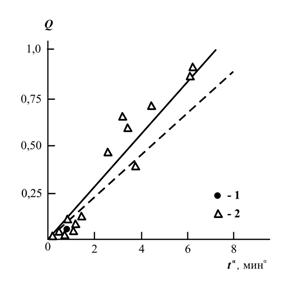
Рис.4.11. Зависимость степени конверсии Q при t=50 мин. от активного времени tα для реакции переэтерификации без наполнителя (1) и в присутствии оксидов металлов (2). Штриховой линией показана зависимость Q(tα) для реакции переэтерификации в присутствии слюды [43].
Рассмотрим физические аспекты формирования молекул гептилбензоата, которые, как показано выше, являются фракталоподобными объектами. Увеличение Df означает уменьшение стерического фактора ρ(ρ≤1), который дает вероятность реакции при первом контакте реагентов. Величины Df и ρ связаны между собой соотношением (2.41). Указанное соотношение для реакции в присутствии СаО (Df=1,54) дает ρ=0,852, а для реакции в присутствии ВеО (Df=2,29)-ρ=0,042. Таким образом, низкие Df соответствуют диффузионно-лимитированному механизму агрегации (ρ→1), а большие Df – химически лимитированному (ρ→0) [6]. Важно отметить определяющую роль структуры фракталоподобной молекулы гептилбензоата, характеризуемой размерностью Df, как в определении типа агрегации (уравнение (2.41)), так и в определении типа странной (аномальной) диффузии (уравнение (2.45)). Введение того или иного наполнителя – катализатора является только способом регулирования структуры, причем не единственным. К другим способам можно отнести вариацию растворителя, изменение температуры реакции или соотношения реагентов и т.д. [11].
Следовательно, рассмотренные выше результаты показали возможность регулирования структуры продукта реакции переэтерификации (молекулы гептилбензоата) изменением наполнителя-катализатора, в качестве которого использованы наночастицы оксидов металлов. Изменение указанной структуры приводит к существенной вариации активного времени tα, т.е., действительной продолжительности химической реакции, а именно для рассмотренных условий реакции примерно в 20 раз. В свою очередь, это сказывается на вариации основных показателей реакции переэтерификации. Зависимость степени конверсии от активного времени для всех использованных оксидов металлов описывается общей линейной корреляцией [43].
Литература к Главе 4
1. Васнев В.А., Нафадзокова Л.Х., Тарасов А.И., Виноградова С.В., Лепендина О.Л. Высокомолек. соед. А. 2000, т. 42, № 12, с. 2065-2071.
2. Burya A.I., Naphadzokova L. Kh., Kozlov G.V. Proceedings of IV-th Ukrainian – Polish Scientific Conf. “The Polymers of Special Application”. Dnepropetrovsk, 2006, p. 88.
3. Нафадзокова Л. Х., Козлов Г. В., Шустов Г. Б. Катализ в промышленности, 2007, №5, с.61-63.
4. Иванова В.С. В сборн.: Труды Междунар. междисциплинарного симпозиума «Фракталы и прикладная синергетика, ФиПС-03» М., Изд-во МГОУ, 2003, с. 271-274.
5. Naphadzokova L. Kh., Kozlov G.V., Zaikov G.E. Oxidation Commun., 2007, v.30, N4, p.788-792.
6. Шогенов В.Н., Козлов Г.В. Фрактальные кластеры в физико-химии полимеров. Нальчик, Полиграфсервис и Т., 2002, 270 с.
7. Фомченко Г.П. Химия. М., Высшая школа, 1993, 368 с.
8. Family F. J. Stat. Phys., 1984, v. 36, № 5/6, p. 881-896.
9. Нафадзокова Л.Х., Козлов Г.В. В сборн. стат. I Междунар. научн.-техн. конф. «Аналитические и численные методы моделирования естественнонаучных и социальных проблем». Пенза ПГУ, 2006, с. 190-193.
10. Weitz D.A., Huang J.S., Lin M.Y., Sung J. Phys. Rev. Lett, 1985, v. 54, № 13, p. 1416-1419.
11. Козлов Г.В., Шустов Г.Б. В сборн.: Успехи в области физико-химии полимеров. Ред. Заиков Г.Е. и др. М., Химия, 2004, с. 341-411.
12. Нафадзокова Л.Х., Козлов Г.В. В сборн. стат. VIII Междунар. научн.-практ. конф. «Новые химические технологии: производство и применение» Пенза, ПГУ, 2006, с. 63-66.
13. Нафадзокова Л.Х., Козлов Г.В., Лигидов М.Х., Пахомов С.И. Известия ВУЗов. Химия и химическая технология, 2008, (в печати).
14. Kozlov G.V., Dolbin I.V., Zaikov G.E. Oxidation Commun., 2005, v. 28, № 1, p. 143-152.
15. Kozlov G.V., Zaikov G.E. The Structural Stabilization of Polymers: Fractal Models. Leiden-Boston, Brill Academic Publishers, 2006, 345 p.
16. Halsey T.C., Jensen M.H., Kadanoff L.P., Procaccia I., Shraiman B.I. Phys. Rev. A, 1986, v. 33, № 2, p. 1141-1151.
17. Федер Е. Фракталы. М., Мир, 1991, 248 с.
18. Болотов В.Н. Письма в ЖТФ, 1995, т. 21, № 10, с. 82-84.
19. Зеленый Л.М., Милованов А.В. Успехи физических наук, 2004, т. 174, № 8, с. 809-852.
20. Нигматуллин Р.Р. Теоретическая и математическая физика, 1992, т. 90, № 3, с. 354-367.
21. Баланкин А.С. Синергетика деформируемого тела. М., Изд-во Министерства Обороны СССР, 1991, 404 с.
22. Шнелл Г. Химия и физика поликарбонатов. М., Химия, 1967, 229 с.
23. Козлов Г.В., Темираев К.Б., Калоев Н.И. Доклады РАН, 1998, т. 362, № 4, с. 489-492.
24. Botet R., Jullien R., Kolb M. Phys. Rev. A, 1984, v. 30, № 4, p. 2150-2152.
25. Kobayashi M., Yoshioka T., Imai M., Itoh Y. Macromolecules, 1995, v. 28, № 22, p. 7376-7385.
26. Kozlov G.V., Ozden S., Malkanduev Yu.A., Zaikov G.E. In book: Fractals and Local Order in Polymeric Materials. Ed. Kozlov G.V., Zaikov G.E. New York, Nova Science Publishers, Inc., 2001, p. 11-19.
27. Kozlov G.V., Ozden S., Malkanduev Yu.A., Zaikov G.E. Russian Polymer News, 2002, v. 7, № 3, p. 38-44.
28. Hentschel H.G.E., Deutch J.M. Phys. Rev. A, 1984, v. 29, № 3, p. 1609-1611.
29. Naphadzokova L.Kh., Kozlov G.V., Zaikov G.E. J. Balkan Tribologic. Assoc., 2007, v. 13, N4, p. 329-333.
30. Argyrakis P., Kopelman R. Phys. Rev. B, 1984, v. 29, № 1, p. 511-514.
31. Kopelman R., Klymko P.W., Newhouse J.S., Anacker L.W. Phys. Rev. B, 1984, v. 29, № 6, p. 3747-3748.
32. Anacker L.W., Kopelman R. J. Chem. Phys., 1984, v. 81, № 12, p. 6402-6403.
33. Rammal R., Toulouse G. J. Phys. Lett. (Paris), 1983, v. 44, № 1, p. L13-L22.
34. Коршак В.В., Виноградова С.В. Неравновесная поликонденсация. М., Наука, 1972, 695 с.
35. Нафадзокова Л.Х., Васнев В.А., Тарасов А.И. Пласт. массы, 2001, № 3, с. 39-41.
36. Grassberger P., Procaccia I. J. Chem. Phys., 1982, v. 77, № 12, p. 6281-6284.
37. Meakin P., Stanley H.E. J.Phys. A, 1984, v. 17, № 1, p. L173-L177.
38. Redner S., Kang K. J.Phys. A, 1984, v. 17, № 2, p. L451-L455.
39. Kang K., Redner S. Phys. Rev. Lett., 1984, v. 52, № 12, p. 955-958.
40. Kozlov G.V., Bejev A.A., Lipatov Yu.S. J. Appl. Polymer Sci., 2004, v. 92, № 4, p. 2558-2568.
41. Vilgis T.A. Physica A, 1988, v. 153, № 2, p.341-354.
42. Alexander S., Orbach R. J. Phys. Lett. (Paris), 1982, v. 43, № 17, p. L625-L631.
43. Нафадзокова Л.Х., Козлов Г.В., Лигидов М.Х., Пахомов С.И. Известия ВУЗов. Химия и химическая технология, 2007 (в печати).
44. Нафадзокова Л.Х., Козлов Г.В Химическая технология, 2006, №8, с. 32-36.
