
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Объем
Сведения из теории
Объем прямоугольного параллелепипеда – V = abc.
Объем пирамиды – 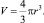
Объем прямого кругового цилиндра – V = 2πr2h.
Объем конуса – 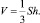
Объем шара – 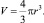
Задача 323. Сколько коробок в форме прямоугольного параллелепипеда размерами 30×40×50 (см) можно поместить в кузов машины размерами 2×3×1,5 (м)?
Ответ: 150.
Задача 324. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см×40 см?
Ответ: 90.
Задача 325. Размеры кирпича 25×12×6,5 (см). Найдите вес одного кирпича в граммах, если объемный вес кирпича равен 1700 кг/м3.
Ответ: 3315.
Задача 326. Какова должна быть площадь кабинета высотой 3,5 м для класса в 28 человек, если на каждого ученика нужно 7,5 м3 воздуха?
Ответ: 60.
Задача 327. Прямолинейный участок дороги шириной 10 м и длиной 100 м требуется покрыть асфальтом толщиной 5 см. Сколько потребуется машин асфальта, если объемный вес асфальта равен 2,4 т/м3, а грузоподъемность одной машины – 5 тонн?
Ответ: 24.
Задача 328. Пирамида Хеопса имеет форму правильной четырехугольной пирамиды, сторона основания которой равна 230 м, а высота около 138 м. Найдите ее объем в кубических метрах.
Ответ: 2433400.
Задача 329. В цилиндрический сосуд, в котором находится 6 дм3 воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали в кубических дециметрах?
Ответ: 3.
Задача 330. Воду, находящуюся в цилиндрическом сосуде на уровне 12 см, перелили в цилиндрический сосуд, в два раза большего диаметра. На какой высоте будет находиться уровень воды во втором сосуде?
Ответ: 3.
Задача 331. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Ответ: 1,125.
Задача 332. Воду, заполняющую всю коническую колбу высотой 12 см, перелили в цилиндрический сосуд, радиус основания которого равен радиусу окружности конической колбы. На какой высоте от основания цилиндрического сосуда будет находиться поверхность воды?
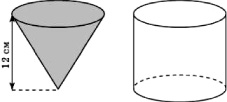
Задача 333. Медный прямоугольный параллелепипед, ребра которого равны 20 с, 20 см и 10 см, переплавлен в шар. Найдите радиус шара. (Примите π ≈ 3.)
Ответ: 10.
Задача 334. Сколько нужно взять медных шаров радиуса 2 см, чтобы из них можно было выплавить шар радиуса 6 см?
Ответ: 27.
Задача 335. Найдите радиус шара, который можно выплавить из трех медных шаров радиусов 3 см, 4 см и 5 см.
Ответ: 6.
Задача 336. Мякоть вишни окружает косточку толщиной, равной диаметру косточки. Считая шарообразной форму вишни и косточки, найдите отношение объема мякоти к объему косточки.
Ответ: 26.
Задача 337. Профиль русла реки имеет форму равнобедренной трапеции, основания которой равны 10 м и 6 м, а высота – 2 м. Скорость течения равна 1 м/с. Какой объем воды проходит через этот профиль за 1 мин? Ответ дайте в кубических метрах.
Ответ: 960.
Задача 338. Чугунная труба имеет длину 2 м и внешний диаметр 20 см. Толщина стенок трубы равна 2 см. Найдите вес трубы, если удельный вес чугуна примерно равен 7,5 г/см3. Ответ дайте в килограммах. (Примите π ≈ 3.)
Ответ: 162.
Задача 339. Какой объем краски потребуется, чтобы окрасить внешнюю поверхность цилиндрической трубы диаметра 1 м и длины 10 м слоем краски в 1 мм? Ответ дайте в кубических дециметрах. (Примите π ≈ 3.)
Ответ: 30.
Задача 340. Какой объем краски потребуется, чтобы окрасить поверхность шара радиуса 1 м слоем краски в 0,5 мм? Ответ дайте в кубических дециметрах. (Примите π ≈ 3.)
Ответ: 6.
Задача 341. Квадратный лист бумаги со стороной 6 см перегнули по пунктирным линиям, показанным на рисунке, и сложили треугольную пирамиду. Найдите ее объем.
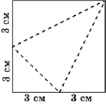
Ответ: 9.
Задача 342. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).
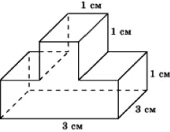
Ответ: 12.
Задача 343. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).
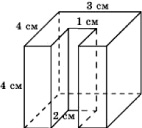
Ответ: 40.
Задача 344. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).
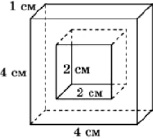
Ответ: 12.
Задача 345. В каждой грани медного куба с ребром 6 см проделали сквозное квадратное отверстие со стороной квадрата 2 см. Найдите вес оставшейся части, считая удельный вес меди приблизительно равным 0,9 г/см3.
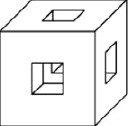
Ответ: 144.
Задача 346. Найдите объем детали, изображенной на рисунке, составленной из двух частей цилиндров. (При-
мите π ≈ 3).
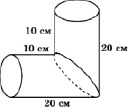
Ответ: 2250.
Задача 347. Найдите объем детали, изображенной на рисунке, вырезанной из цилиндра. (Примите π ≈ 3.)
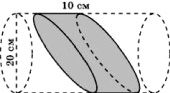
Ответ: 3000.
Задача 348. Диаметр Солнца примерно в 400 раз больше диаметра Луны. Во сколько раз объем Солнца больше объема Луны?
Ответ: 64000000.
