Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

2.1. Основные принципы фрактальной модели процессов газопереноса

Диффузия на фрактальных объектах, называемая также аномальной [1] или странной [2], имеет ряд специфических особенностей, исследование которых начато более 20 лет тому назад [3] и продолжается до сих пор. Эти особенности полностью относятся и к полимерам, которые обладают фрактальной структурой. Кроме того, на указанные особенности налагается специфика структуры полимеров, в которых диффузия реализуется через микрополости флуктуационного свободного объема [4; 5]. Эти обстоятельства делают процессы диффузии в полимерных мембранах достаточно сложными и зависящими от значительного числа параметров. Сначала мы рассмотрим трактовку процессов газопереноса в рамках кластерной модели. Поскольку весь флуктуационный свободный объем полимера концентрируется в рыхлоупакованной матрице [6], то следует ожидать, что повышение ее относительной доли j_р.м. приведет к увеличению коэффициентов диффузии D или проницаемости Р. Действительно, такая корреляция получена в работе [7], которая аналитически выражается следующими простыми соотношениями [8]:

,                                         (2.2)

где   и  - константы, f_c - относительный флуктуационный свободный объем.

Наличие скачка коэффициента диффузии D при температуре плавления Т_пл полиэтиленов является хорошо установленным экспериментальным фактом [9]. Авторы [9] предложили теоретическую модель для описания температурной зависимости D, которая предполагает два разных уравнения для температурных интервалов T < T_пл и T > T_пл. Отметим, что эта модель не учитывает структурных различий аморфной фазы полиэтиленов в аморфно-кристаллическом (T < T_пл) и вязкотекучем (T > T_пл) состояниях. В работах [10-13] рассмотрено описание зависимости D(T) и, в частности, скачка D при Т_пл, в рамках кластерной модели, которая учитывает указанные выше структурные различия.

Рассмотрим физические основы существования скачка D при Т_пл в предлагаемой трактовке. Модель [9] предполагает одинаковую структуру аморфной фазы в аморфно-кристаллическом полиэтилене и его расплаве. В этом случае роль кристаллической фазы сводится к уменьшению D, пропорциональному степени кристалличности. Кроме того, авторы [9] предположили, что лимитирующей стадией диффузии газов в аморфно-кристаллических полиэтиленах является перенос через места контакта кристаллитов, что следует считать достаточно произвольным предположением. Известно [14], что переход кристаллической фазы в аморфную является наиболее плотноупакованной частью некристаллических областей полиэтиленов и поэтому нет оснований ожидать как непосредственного контакта кристаллитов, так и повышенной рыхлости в местах таких контактов, если они существуют [11].

В рамках предлагаемой трактовки структура аморфной фазы аморфно-кристаллического полиэтилена и его расплава различаются наличием в первой областей локального порядка (кластеров), через которые процессы газопереноса также не реализуются. Появление этих областей при Т £ Т_пл обусловлено процессом кристаллизации и вызванным этим процессом натяжением цепей в аморфных прослойках [15]. При Т > Т_пл также сохраняется некоторая доля областей локального порядка, но в этом случае он будет динамическим, с небольшим временем жизни [16]. Скачок D при Т_пл в рамках самых общих физических представлений обусловлен спецификой изменения параметра порядка при критической температуре Т_кр (для полиэтиленов Т_кр = Т_пл). На рис. 2.1 показана схематическая температурная зависимость параметра порядка j(Т), из которой следует очень быстрый рост j в узком интервале температур Т £ Т_пл [17]. Как отмечалось в предыдущей главе, для описания зависимости j_кл(Т) (параметра порядка) может быть использована концепция термического кластера, где величина j_кл дается уравнением [18]:

,                                            (2.3)

где индекс b_Т = 0,40 [13].

Для принятого в работе [9] температурного интервала скачка D примерно 5К и Т_пл = 403К [19], получим j_кл = 0,176, что и является причиной указанного скачка [12].

Еще проще и нагляднее продемонстрировать физический смысл скачка D при Т = Т_пл можно с помощью уравнений (2.1) и (2.2). Хотя эти уравнения были получены для описания диффузии кислорода для ряда аморфных и аморфно-кристаллических полимеров [8], тем не менее, близость диаметров молекул для О₂ и СН₄ [5] позволяет использовать их для предварительного анализа диффузии СН₄. Так, для Т = Т_пл - 5 К величина j_р.м. согласно модели [20] равна ~ 0,827, а при Т > T_пл уравнение (1.19) дает j_р.м. » 0,933. Расчет по уравнению (2.1) дает различие lg D для этих состояний ~ 0,61, а расчет по уравнению (2.2) при f_c = 0,091 при Т = Т_пл - 5К и f_c = 0,113 при T > T_пл дает различие lgD » 0,60 для этих же состояний. Эти результаты превосходно согласуются с экспериментальной разницей lgD, равной ~ 0,63 [9].

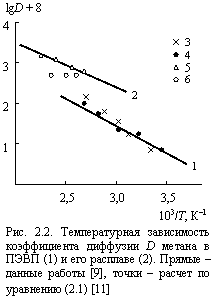
Сравнение температурных зависимостей коэффициента диффузии для ПЭВП и его расплава, рассчитанной по уравнению (2.1) и полученной экспериментально [9], приведено на рис. 2.2. Получено неожиданно хорошее (с учетом аппроксимационного характера уравнения (2.1) [8]) соответствие теории и эксперимента, а постоянная величина D при T > T_пл обусловлена принятым в [11] условием j_р.м. = const = 0,933 в этом температурном интервале. Важно также отметить, что использована одна и та же константа , равная 3,65 ´ 10^-11 м²/с для обоих температурных интервалов [10].

Следовательно, кластерная модель позволяет объяснить поведение коэффициента диффузии как функции температуры в рамках единого структурного подхода как выше, так и ниже Т_пл. Предложенная авторами [10-13] трактовка объясняет скачок D при Т_пл как результат формирования (распада) областей локального порядка (кластеров), непроницаемых для газопереноса. Рассматриваемая трактовка дает не только качественное, но и количественное описание зависимости D(Т) во всем использованном интервале температур.

Авторы [22] предложили фрактальную модель диффузии газов на примере аморфно-кристаллического полиэтилена, учитывая его более сложную структуру по сравнению с аморфными полимерами. Присутствие кристаллитов в диффузионной среде снижает суммарную скорость переноса через равные объемы. Чем выше степень кристаллитов капилляров или пустот, тем ниже коэффициенты диффузии и растворимости и, следовательно, проницаемость [4; 23]. Однако, обычно величина D не прямо пропорциональна содержанию аморфной фазы, как в случае растворимости [9], а носит более сложный характер [4].

В связи с этим были введены эмпирические коэффициенты, учитывающие два основных фактора, влияющих на диффузионные характеристики аморфно-кристаллических полимеров. Первый из них - коэффициент непрямолинейности или извилистости t - учитывает тот факт, что путь молекулы пенетранта в аморфной фазе отличается от прямолинейного, что снижает коэффициент диффузии D (t ³ 1). Второй коэффициент b_м учитывает снижение скорости диффузии, вызванное ограничением подвижности цепей в аморфной фазе из-за наличия кристаллитов. Коэффициент b_м называется коэффициентом неподвижности цепей [4]. С учетом этих фактором величина D аморфно-кристаллического полимера записывается так [4]:

,                                                         (2.4)

где D_а - коэффициент диффузии соответствующего полностью аморфного полимера; j_а - относительная доля аморфной фазы.

Наличие двух эмпирических коэффициентов в уравнении (2.4) (t и b_м) делает теоретическое предсказание D практически невозможным.

Кроме указанных факторов, на величину D существенное влияние оказывает размер молекулы d_м пенетранта [4; 5; 23]. В общем случае увеличение d_м приводит к очень резкому снижению D. Достаточно простые корреляции D(d_м) можно получить только для диффузии простейших газов (одно- и двухатомных с низкой критической температурой) [5].

Попытки решить указанные выше проблемы предпринимались с помощью фрактального анализа на примере горных пород [24; 25]. Для полимеров применение такого подхода имеет достаточно очевидные причины. Во-первых, как отмечалось выше, структура твердых полимеров представляет собой фрактальный объект. Во-вторых, фрактальная размерность отражает оба указанных выше фактора: увеличение этой размерности означает уменьшение и t, и b_м [26; 27]. Таким образом, фрактальный анализ представляет возможность теоретического прогнозирования диффузионных характеристик [22].

В работе [5] приведены величины D для ПЭНП и ПЭВП и нескольких газообразных пенетрантов: N₂, O₂, CO, CO₂ и HCl. Для теоретического описания D авторы [22] использовали уравнение, приведенное в работе [24] для анализа диффузии в горных породах:

,                                  (2.5)

где  - константа, которая в дальнейшем принимается равной величине D для полимерного расплава (  = 3,8 ´ 10^-7 см²/с), что оказалось универсальным значением, F - пористость, l₁ и l₂ - верхний и нижний пределы фрактального поведения, соответственно, D¢ - фрактальная размерность, контролирующая процессы газопереноса.

Рассмотрим определение параметров уравнения (2.5) применительно к полимерам. В качестве F для них естественно использовать флуктуационный свободный объем f_c, через микрополости которого и происходит диффузия газов [28]. Величина f_c может быть оценена из следующего уравнения [6]:

f_c = 0,113 j_а.                                                       (2.6)

В качестве l₁ и l₂ следует принять диаметры микрополости свободного объема d_h и молекулы газа-пенетранта d_м, cоответственно. Объем микрополости флуктуационного свободного объема n_h можно рассчитать так [29]:

,                                           (2.7)

где n_р - коэффициент Пуассона, k - постоянная Больцмана, Е - модуль упругости. Полагая, что микрополость имеет сферическую форму, из известных величин n_h можно рассчитать d_h. Величины d_м в дальнейшем принимались согласно литературным источникам [5; 30; 31]. Поскольку процесс диффузии газов реализуется на молекулярном уровне [9], то в качестве d_s приняты величины спектральной размерности полимерной цепи. Для разветвленного ПЭНП d_s = 1,33, для линейного ПЭВП - d_s = 1,0 [32]. Необходимые для расчета величин D параметры оцененные указанными методами (D_f рассчитана согласно (1.25), d_f - согласно (1.41), приведены в табл. 2.1.

Таблица 2.1

Параметры фрактальной модели диффузии газов в полиэтиленах [22]

Полимер	fc	nh, Å3	dп, Å	Df	ds
ПЭНП	0,060	226	7,56	3,72	1,33
ПЭВП	0,024	50,5	4,58	4,13	1,0

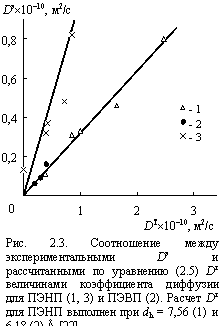
На рис. 2.3 приведено сравнение рассчитанных по уравнению (2.5) D^т и полученных экспериментально [5] D^э величин коэффициента диффузии для ПЭНП и ПЭВП. Как можно видеть, получено превосходное качественное соответствие, но величины D^т примерно в 3 раза превышают экспериментальные значения D^э. Основной причиной указанного количественного несоответствия являются разные образцы полиэтиленов, использованные для оценки механических свойств (уравнения (1.14) и (1.15)) и измерений D. Кроме того, фактором, увеличивающим погрешность, является типичная для фрактальных соотношений сильная степенная зависимость D, описываемая уравнением (2.5) [22].

Рассмотрим эти факторы на примере ПЭНП, для которого анализ размеров микрополости свободного объема методом аннигиляции позитронов дал величину наиболее продолжительной компоненты долговечности позитрона t₃ = 2,2 нс при Т = 293 К [33]. В работе [34] приведена упрощенная формула, позволяющая оценить величину n_h по известным значениям t₃:

t₃ = 7,80n_h + 1,29.                                             (2.8)

Оценка по уравнению (2.8) дает n_h = 124ų или d_h = 6,18 Å. Отметим, что образцы ПЭНП, использованные для измерений D [5] и t₃ [33] имели близкие значения плотности r (0,914 и 0,912 г/см³, соответственно) и, следовательно, близкие величины К, что дает основания для их сравнения. Расчет величин D^T для ПЭНП с использованием d_h = 6,18 Å вместо использованного ранее d_h = 7,56 Å (табл. 2.1) дает гораздо лучшее соответствие между D^т и D^э (рис. 2.3). Еще одним источником завышения величин D^т может быть погрешность оценки n_р согласно соотношению (1.15) [35].

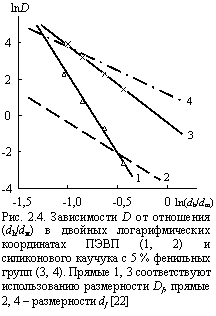
Для оценки величины D согласно уравнению (2.5) авторы [22], использовали размерность D_f в качестве D¢, а не фрактальную размерность структуры d_f. Формальная причина этого заключается в том, что D_f контролирует свойства флуктуационного свободного объема [36] и также следующее экспериментальное наблюдение. Как следует из уравнения (2.5), для одного и того же полимера величины , f_c, D¹ и l₁ являются постоянными и поэтому зависимость D от (d_h/d_м) (или 1/d_м) в двойных логарифмических координатах должна быть прямой с наклоном 2(D¢ - d_s)/d_s. На рис. 2.4 приведена такая зависимость для ПЭВП, где величины D взяты для ряда инертных газов [5]. Как и ожидалось, получена линейная зависимость, указывающая на быстрый спад D по мере увеличения d_м. наклон этой зависимости D » 8, что дает величину D¢ = 5 при d_s = 1,0. Поскольку максимальная величина d_f = d = 3 [37], то наклон зависимости D(d_h/d_м) в двойных логарифмических координатах при использовании этой размерности не может превышать 4 для линейных полимеров и ~ 2,51 - для разветвленных. Таким образом, использование d_f для ПЭВП не согласуется с экспериментальными результатами. В то же время величины D_f и d_f однозначно связаны соотношением (1.41). Исходя из D » 8 и D_f = 5 (рис. 2.4), получим для ПЭВП согласно уравнению (1.41) d_f » 2,75 и n_р » 0,375, что превосходно согласуется с оценками, сделанными другими методами [29].

На рис. 2.4 также приведена зависимость D(d_h/d_м) в двойных логарифмических координатах для силиконового каучука с 5 % фенильных групп в случае диффузии инертных газов [5]. Величина d_h для этого полимера выбрана типичной для каучуков (~ 10 Å) [22]. Как можно видеть, наклон графика D для сшитого каучука вдвое меньше, чем для линейного ПЭВП, и также превышает предельно допустимую величину D » 2,51 при использовании d_f. Таким образом, для разветвленных полимеров спад D по мере роста d_м значительно медленнее, чем для линейных, и причиной этого являются разные значения спектральной размерности d_s для указанных классов полимеров. На рис. 2.4 также приведены теоретические зависимости, использующие размерность d_f, а не D_f (прямые 2 и 4). Как можно видеть, их наклон значительно меньше, чем для экспериментальных зависимостей, т.е., они наглядно демонстрируют, что использование d_f не дает соответствия теории и эксперимента [22].

Тем не менее, как показано в [26; 27] зависимость коэффициента проницаемости Р от (1/d_м) может резко изменить свой наклон. Такое изменение наблюдалось и ранее и было объяснено изменением подвижности цепей [23]. В предлагаемой трактовке это означает, что при d_м < (где  - некоторое критическое значение d_м [26]) взаимодействие молекул газа-пенетранта со стенками микрополостей свободного объема невелико или отсутствует и тогда процесс газопереноса контролируется размерностью d_f. При d_м >  на процесс газопереноса сильно влияет взаимодействие молекул газа со стенками микрополостей, которые представляют собой поверхность макромолекул с высокой молекулярной подвижностью вследствие расстеклованного состояния аморфной фазы полиэтиленов и, следовательно, высоким значением D_f. Иначе говоря, при d_м <  газоперенос реализуется через систему микрополостей, сформированных совокупным действием аморфной и кристаллической фаз, и процесс контролируется размерностью d_f. При d_м <  основным механизмом газопереноса является взаимодействие молекул газа со стенками микрополостей расстеклованной аморфной фазы, поэтому процесс контролируется размерностью D_f. По существу, в процессе газопереноса наблюдается два разных режима для d_м <  и d_м > : структурный и молекулярный, соответственно [26; 27]. К вопросу взаимодействия газ - полимер мы неоднократно будем обращаться ниже вследствие важности этого фактора.

В уравнении (2.5) размер молекул газа выражен их диаметром d_м, хотя для этой же цели используются и другие параметры: молекулярная масса М [4] или мольный объем [38]. В работе [4] использована следующая зависимость D от размера молекул газа-пенетранта:

,                                                      (2.9)

где k_м и b_м - константы.

Авторы работы [39] обнаружили систематическое увеличение показателя b_м с ростом Т_с полимеров и объяснили наблюдаемую закономерность увеличением кинетической жесткости цепи по мере повышения Т_с. Однако, поскольку константы k_м и b_м являются эмпирическими, то это затрудняет прогнозирование величины D с помощью уравнения (2.9).

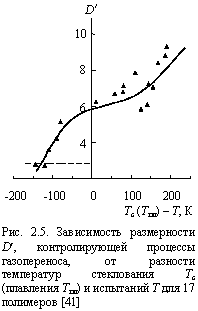
Авторы работы [40] обнаружили V-образную зависимость D от величины Т_с, соответствующую по форме зависимости частоты корреляции парамагнитных зондов n_с от Т_с. На основе этого соответствия был сделан вывод, что увеличение D обусловлено ростом относительного свободного объема про мере повышения Т_с. Однако и это объяснение носит качественный характер. Авторы [41] объяснили наблюдаемые зависимости D(T_c) в рамках одной количественной трактовки, а именно, фрактальной модели процессов газопереноса в полимерах [22]. Отметим, что авторы [41] использовали модифицированный критерий выбора размерности в уравнении (2.5): при (d_h/d_м) > 1,70 в качестве D¢ выбирается d_f, а при (d_h/d_м) £ 1,70 - D_f.

Нетрудно видеть, что уравнения (2.5) и (2.9) дают одинаковую функциональную форму зависимости D от размера молекул газа-пенетранта: в силу степенной зависимости величина D быстро снижается по мере роста d_м или М. Однако, уравнение (2.5) не содержит эмпирических (подгоночных) параметров, что позволяет использовать его для прогнозирования D. На рис. 2.5 приведена зависимость D¢ от разности температур стеклования Т_с (или плавления Т_пл для аморфно-кристаллических полимеров) и испытаний Т для 17 полимеров. Как и в случае зависимости b_м(Т_с - Т) [39], наблюдается сигмоидальная зависимость D¢[T_c(T_пл) - Т), хотя и несколько иной формы. Горизонтальные штриховые линии показывают предельные величины D¢ для реальных полимеров: d_f = 2,95 и D_f = 10,1 [42]. Как отмечалось выше, величина t₃ характеризует размер микрополости свободного объема [34]. На рис. 2.6 приведена зависимость t₃ от разности [T_c (T_пл) - Т] для 13 полимеров. Как и ранее [39; 43], получена V-образная зависимость с минимумом t₃ при Т_с = T (T_пл = Т). Эта зависимость позволяет прогнозировать величину объема микрополости свободного объема n_h согласно уравнению (2.8).

И последнее замечание необходимо сделать относительно выбора величины d_h. Как было показано в работе [44], при расчете D по уравнению (2.5) следует учитывать не номинальный диаметр микрополости d_h, а его эффективное значение . Это обусловлено тем, что стенки микрополости представляют собой шероховатые на атомном уровне поверхности сегментов макромолекул, колеблющихся вокруг своего положения равновесия [45; 46]. Условие D¢ = d_f означает, что молекула газа-пенетранта не взаимодействует со стенками микрополости и тогда в качестве  принимается [44]:

 = d_h + Dd_h,                                                   (2.10)

где Dd_h - удвоенная амплитуда колебаний сегментов, окружающих микрополость.

При D¢ = D_f указанное взаимодействие реализуется и тогда [44]:

 = d_h - Dd_h.                                                   (2.11)

Следует предположить, что глубина проникновения молекулы газа-пенетранта в стенку микрополости свободного объема будет равна амплитуде колебаний l_к сегмента, окружающего эту микрополость, поскольку в собственно сегмент молекула газа проникать не может (эффект исключенного объема). В рамках фрактального анализа это означает, что существует единственный линейной масштаб l_к, определяющий расстояние взаимопроникновения молекулы газа в стенку микрополости. В этом случае можно записать [47]:

,             (2.12)

где а - нижний линейный масштаб фрактального поведения, r_h - радиус микрополости свободного объема, d_п - размерность поверхности стенки микрополости.

Величина а принимается равной длине скелетной связи цепи полимера l₀, поскольку при а < l₀ макромолекула теряет свою индивидуальность [48], а величина d_п может быть оценена так [49]:

d_п = d_f - 0,14.                                                      (2.13)

Таким образом, теперь получен полный набор параметров уравнения (2.5) (f_c, , d_м [30], D¢ и d_s = 1,0), что позволяет прогнозирование величины D для произвольного линейного полимера. Для сшитых (разветвленных) полимеров следует использовать d_s = 1,33. В работе [40] были получены эмпирические аппроксимации, позволяющие описать зависимость D от Т_с. В случае диффузии О₂ они имеют вид [40]:

lgD = - (3,44 + 0,013 T_c) для Т £ 298К         (2.14)

и

lg D = - (9,4 - 0,0058 T_c) для Т ³ 298К.       (2.15)

На рис. 2.7 приведено сравнение зависимостей lgD от Т_с (или Т_пл для диффузии О₂, рассчитанных по уравнениям (2.14) и (2.15) (прямые линии) и уравнению (2.5) (точки). Как можно видеть, получено хорошее соответствие обоих наборов данных, причем расчет по уравнению (2.5) по точности примерно соответствует экспериментальному определению D [40].

В табл. 2.2 приведено сравнение экспериментальных и рассчитанных по уравнению (2.5) величин D для пяти полимеров и трех газов (Ar, N₂, O₂). Как можно видеть, получено удовлетворительное соответствие теории и эксперимента, которое подтверждает корректность предложенной трактовки.

Таким образом, предложенная фрактальная модель адекватно объясняет зависимость коэффициента диффузии от температуры стеклования (плавления) полимеров. Поскольку при расчете величины D в рамках фрактальной модели используются только структурные параметры, определяемые независимыми методами, то появляется возможность прогнозирования величины D с помощью двух калибровочных графиков. Такой расчет дает удовлетворительное соответствие теории и эксперимента [41].

Как известно [4; 5; 21], растворимость газов играет важную роль в процессах переноса для полимеров, в значительной степени определяя их газопроницаемость. Авторы работы [31] предложили следующее корреляционное соотношение для описания коэффициента растворимости газов s в полимерах:

lgs = K₁ + K₂(e/k)_эф,                                           (2.16)

где K₁ и K₂ - изотермические константы для данного полимера, (e/k)_эф - характеристическая силовая постоянная потенциала Леннарда-Джонса, рассчитанная для взаимодействия газ - газ.

Таблица 2.2

Сравнение экспериментальных и рассчитанных по уравнению (2.5) коэффициентов диффузии D [ 41]

Полимер	D, см2/с
	Расчет по уравнению (2.5)	эксперимент
Полидиметилсилоксан	109	108
	79	94
	107	115
Поливинилтриметилсилан	7,1	4,8
	3,9	3,6
	9,9	7,6
Поликарбонат	2,9	0,2
	1,6	1,3
	5,3	0,2
Поливинилацетат	0,05	0,16
	0,04	0,06
	0,07	0,50
Натуральный каучук	5,8	13,6
	5,3	11,7
	7,5	17,3

Соотношение (2.16) позволяет достаточно точный расчет величины s [31], но наличие двух эмпирических констант, тем более различающихся для разных температур, делает прогнозирование величины s согласно этому методу затруднительным. Кроме того, в уравнении (2.16) отсутствуют какие-либо структурные характеристики полимера, хотя они могут входить в константы K₁ и K₂ неявным образом. В работах [45; 46] была предложена новая фрактальная модель микрополости флуктуационного свободного объема, которая отличается от традиционных, вкратце описанная выше. Показано, что микрополость моделируется D_f-мерной (а не трехмерной) сферой и размерность ее стенок примерно равна D_f, т.е., связана с энергетическими характеристиками структуры [50]. На основе этой трактовки авторы работы [51] предложили фрактальную модель для количественного описания растворимости газов с учетом как структуры полимеров, так и структурных характеристик растворяющихся газов.

Предполагается, что растворимость простых газов, не взаимодействующих с полимером, реализуется осаждением их молекул на стенках микрополостей флуктуационного свободного объема, т.е., рассматривается «истинная» сорбция [23]. В этом случае можно записать [52]:

,                                                    (2.17)

где S_м - поперечное сечение молекулы растворяющегося газа.

Поскольку для серии углеводородов С₁ - С₄, рассмотренных в [51], предполагается наличие взаимодействия между молекулами растворяющегося газа [31], то этот фактор может быть охарактеризован с помощью силовой постоянной потенциала Леннарда-Джонса, рассчитанной именно для таких взаимодействий (см. табл. 2.3). Тогда фрактальную формулу для расчета s можно записать в следующем виде [51]:

,                                     (2.18)

где s₀ - константа, - эффективная площадь поперечного сечения молекулы растворяющегося газа, учитывающая возможность различных ориентацией этой молекулы в микрополости свободного объема.

Таблица 2.3

Величины диаметров d_м, эффективных для процессов растворимости диаметров  и силовых постоянных (e/k) для углеводородов С₁ - С₄ [51]

Углеводород	dм, Å [31]	, Å [31]	, Å, уравнение (2.1.9)	(e/k), K [31]
CH4	3,3 ¸ 4,2	3,18 ± 0,14	3,30	154,7 ± 15,6
C2H6	3,7 ¸ 5,2	3,69 ± 0,08	4,06	250 ± 22
C3H8	4,1 ¸ 5,8	4,09 ± 0,08	4,76	305 ± 28
C4H10	4,6 ¸ 6,9	4,40 ± 0,08	5,66	364 ± 35
C2H4	3,6 ¸ 5,5	3,57 ± 0,08	3,82	225 ± 15
C3H6	4,1 ¸ 5,4	3, 68 ± 0,13	4,63	294 ± 32
C4H8 - 1	4,5 ¸ 5,2	4,18	5,36	356
C2H2	3,5 ¸ 5,7	3,38±0,06	3,70	223 ± 23
C3H4 (м)	4,0 ¸ 4,8	3,62±0,07	4,62	321 ± 25
C4H6 (э)	4,4 ¸ 5,0	3,81	5,26	360
С3Н4 (а)	4,6 ¸ 4,9	3,64±0,07	5,38	335 ± 14
С4Н6 (б)	5,0	3,85	5,45	327

Примечание: м - метилацетилен, э - этилацетилен, а - аллен, б - бутадиен.

В справочной литературе диаметры d_м молекул углеводородов даются с большим разбросом, причем максимальный диаметр  может превышать минимальный  в 1,5 раза (например, для С₄Н₁₀, см. табл. 1 работы [31]). По существу, определение эффективного диаметра  означает оценку ориентации молекулы газа в микрополости свободного объема. Чтобы сделать расчет s достаточно точным, необходимо уметь прогнозировать величину  (и, следовательно,  в уравнении (2.18)). В противном случае в силу степенного характера уравнения (2.18) вариация s при изменении d_м в 1,5 раза может достигать одного порядка.

Выполненный обратный расчет, т.е., оценка  по известным значениям s показал систематическое увеличение отношения /  по мере роста (e/k), что показано на рис. 2.8. Аналитически указанное соотношение может быть записано так [51]:

.                                             (2.19)

В дальнейшем для расчета s авторы [51] использовали значения  (и, следовательно, ), оцененные согласно уравнению (2.19).

Отметим, что если размеры и  рассматривать как наибольший и наименьший размеры молекул газа неправильной формы, то увеличение отношения по мере роста (e/k) означает разворот молекулы растворяющегося газа в микрополости свободного объема наибольшим сечением коллинеарно стенке этой микрополости, что описывает ориентацию молекулы газа в процессе сорбции. Такой разворот или увеличение  приводит к росту s согласно формуле (2.18).

Как показали оценки константы s₀ в уравнении (2.18), для полиэтиленов (П) и поливинилтриметилсилана (ПВТМС) она имеет примерно одинаковую величину и равна 4,0 ´ 10^-8, а для каучукообразного полиизопрена (ПИ) s₀ = 4,8 ´ 10^-11, т.е., значительно ниже. Как правило, в уравнениях, подобных формуле (2.18), физический смысл константы определяется при равенстве параметра (в нашем случае s) и константы (в нашем случае s₀) при условии, что остальные члены в правой части уравнения равны единице. Для формулы (2.18) это условие означает [51]:

.                                          (2.20)

Рассмотрим условия реализации критерия (2.20). Минимальное значение d_м для гелия равно 1,8 Å [5], что соответствует = 2,54 Ų. Для минимального значения n_р = - 1, что соответствует очень пористому твердому телу, D_f = 1,33 согласно уравнению (1.25). Тогда для реализации критерия (2.20) необходимо выполнение условия (e/k) = 0,538 К. Эта величина (e/k) примерно на три порядка меньше средней величины (e/k) для углеводородов С₁ - С₄ [31], т.е., это означает практически полное отсутствие взаимодействий между молекулами растворяющегося газа. Таким образом, величина s₀ которая для T < T_c(T_пл) в среднем на 6 ¸ 7 порядков, а для T > T_c(T_пл) даже на 9 ¸ 10 порядков ниже s, определяет минимальную растворимость газа с наименьшим возможным диаметром его молекулы и наименьшей энергией структуры полимера при отсутствии взаимодействий газ - газ. Увеличение d_м, D_f и (e/k), характеризующих указанные факторы, приводит к резкому росту s [51].

На рис. 2.9, 2.10 и 2.11 показаны соотношения литературных s^лит и рассчитанных по уравнению (2.18) s^теор значений коэффициента растворимости углеводородов С₁ - С₄ в ПЭ, ПВТМС и ПИ (D_f = 5,4; 7,0 и 11,0), соответственно. Как можно видеть, получено хорошее соответствие обоих наборов величин s. Среднее расхождение между s^лит и s^теор для трех указанных полимеров составляет ~ 16 %, что вполне достаточно для теоретического прогнозирования коэффициента растворимости газов в полимерах [23].

Таким образом, фрактальная модель позволяет достаточно точное количественное описание растворимости газов в полимерах, Предложенное для этой цели уравнение (2.18) по существу показывает увеличение реальной величины s по сравнению с минимально возможной s₀. Это увеличение контролируется изменением следующих факторов: размера и ориентации молекул растворяющегося газа, взаимодействия между этими молекулами и структуры полимера. Последний фактор наиболее сильно влияет на величину s в силу степенного характера зависимости этого параметра от D_f [51].