Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

РУКОВОДСТВО ПО КЛИНИЧЕСКИМ ИССЛЕДОВАНИЯМ ВНУТРЕННИХ БОЛЕЗНЕЙ

Николаев Н. А.,

ГЛАВА 2. Принципы и методы статистического исследования

Не описывая детально весь статистический инструментарий медико-биологических исследований (этому посвящено большое количество фундаментальных классических руководств), остановимся на ключевых понятиях, которыми должен владеть каждый исследователь.

Статистические данные представляют собой наблюдаемые или измеряемые значения одного или нескольких признаков обследуемой совокупности объектов. Учитывая практическую невозможность непосредственного исследования генеральной совокупности, статистики генеральной совокупности оценивают по репрезентативной выборке.

Для проверки свойств распределения генеральной совокупности выдвигают статистические гипотезы. В качестве нулевой (Н0) обычно выдвигается гипотеза о принадлежности показателей одной генеральной совокупности, в качестве альтернативной (Н1) – о принадлежности показателей различным генеральным совокупностям. Уровнем значимости α, определяющим размер критической области Vk, устанавливают вероятность α менее 0,05.

В статистических пакетах (наиболее употребимы SPSS и Stat Soft Statistica) оценивают p-значение (p-level), принимая р = Р [Z > |zВ||Н0]. При р > α гипотезу Н0 принимают на уровне значимости р. При р < α гипотезу Н0 отклоняют, поскольку при этом zВ попадает в критическую область.

За ошибку первого рода (отклонение правильной гипотезы Н0) принимают величину α, поскольку Р [Z ∈ Vk/Н0] = α. За ошибку второго рода (неверное принятие Н0, когда верна альтернативная Н1) принимают β, вероятность которой рассчитывали:

β = Р [Z ∈ V/Vk/Н1].

Мощность критерия μ(Vk, Θ), расцениваемую как вероятность отклонения Н0 при конкретном Θ принимают равной α, так как

μ(Vk, Θ) = Р [Z ∈ Vk/Н0] = α.

Исследователь должен описать выполненный статистический анализ. Акцент следует сделать на том, какие статистические анализы, сравнения и тесты были запланированы, а не на тех, которые были фактически использованы.

Если критические измерения за время исследования выполнялись несколько раз, укажите все конкретные измерения, запланированные в качестве основы для сравнения исследуемого препарата и контроля (например, среднее значение нескольких измерений, сделанных в течение всего исследования; значения, полученные в определенное время; только по завершившим исследование пациентам, или последние значения в процессе лечения и т.д.).

Аналогично, если возможно использование нескольких аналитических подходов, например, если допускается проведение как оценки изменений показателя по отношению к исходному уровню, так и анализ таблиц дожития, конкретно укажите запланированный подход.

Если имелись какие-либо запланированные причины для исключения из анализа пациентов, по которым получены данные, они должны быть описаны. Если имеются какие-либо подгруппы пациентов, результаты которых должны рассматриваться отдельно, они должны быть указаны.

Если при анализе ответов должны были использоваться категориальные показатели (шкалы общей оценки состояния, оценки степени тяжести, оценки степени выраженности), они должны быть правильно определены и описаны.

Должны быть описаны частота и характер любого запланированного промежуточного анализа, любые конкретные обстоятельства, при которых исследование должно было быть прекращено, и любые статистические корректировки, применяемые вследствие выполнения промежуточных анализов.

Определение объемов выборок

Обязательно следует представить запланированный объем выборки и обоснование его выбора.

Методы расчета объема выборки следует представлять вместе со всеми формулами и промежуточными выкладками или указанием источника, где это приведено.

Должны быть приведены все исходные значения, используемые в расчетах, а также объяснения, как они были получены.

Минимальный объем выборки (с учетом обычно принятых в биологических и медицинских клинических исследованиях пределов ошибок α = 0,05 и β ≤ 0,1) определяют решением системы уравнений:

{Р [Z ∈ Vk/Н0] = 0,05; Р [Z ∈ V/Vk/Н1] ≤ 0,1.

Необходимый объем выборок можно рассчитать по формуле:

N = ([p1(100 – p1)] + [p2(100 – p2)])∙7,9/(p2 – p1)2,

где N – число наблюдений, достаточных для получения значимых выводов; p1 – ожидаемое значение основного критерия оценки для группы исследования; p2 – для группы сравнения.

Требуемое число наблюдений для получения значимых различий в независимых выборках можно определять как

n1,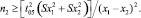

Требуемое число наблюдений для получения значимых различий показателей в связанных выборках устанавливают по формуле:

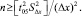
В исследованиях, предназначенных для демонстрации различия между методами лечения, должна быть указана величина клинически значимого отличия, которое исследование призвано определить.

При исследовании активным контролем, предназначенном для демонстрации того, что новая терапия, по крайней мере, так же эффективна, как и стандартная терапия, в определении объема выборки следует указать разницу между методами лечения, которая бы рассматривалась, как неприемлемо большая, и которую исследование призвано исключить.

Проверка распределений

Гипотезы о виде распределения можно проверить используя критерии Shapiro-Wilkin и χ2 Kolmogorov-Smirnov χ2.

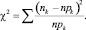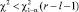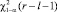По формуле для принятого уровня значимости α гипотеза Н0 признаётся согласующейся с результатами наблюдений при , где  – квантиль порядка 1 – α распределения χ2 с (r – l – 1) степенями свободы; l – число неизвестных параметров распределения, оцениваемых по выборке. Гипотезу Н0 отклоняют при .

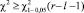Если распределение сравниваемых признаков удовлетворяет требованиям проведения параметрического исследования, целесообразно применять t-критерий Student. Расчет t-критерия в связанных выборках выполняют как

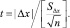
В независимых выборках для расчетов t-критерия используют формулу:

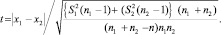
В случаях, когда распределение сравниваемых признаков не удовлетворяет требованиям проведения параметрического исследования, а также при небольших объемах выборок (n < 30) и/или когда поставленные задачи не могут быть решены параметрическими методами исследования, применяют непараметрические методы.

Проверка гипотез о принадлежности независимых выборок однородным генеральным совокупностям

Для проверки гипотезы Н0 о принадлежности двух независимых выборок (объемов n1 и n2) однородным генеральным совокупностям обычно используют критерий серий Wald-Wolfowitz (Wald-Wolfowitz runs test) и критерий Mann-Withney (Mann-Withney U test). При значительных (n > 20) объёмах выборок, вычисления выполняют, используя статистику Z.

Статистику Z критерия Wald-Wolfowitz рассчитывают по формуле:

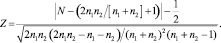
Гипотезу Н0 принимают на уровне значимости α, если выборочное значение zВ статистики Z, удовлетворяет неравенству |zВ| ≤ u1–α/2, где u1–α/2 – квантиль нормального распределения (N 0, 1) с одной степенью свободы порядка 1 – α/2; гипотезу Н0 отклоняли, если |zВ| < u1–α/2.

Статистику Z критерия Mann-Withney вычисляют как:

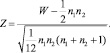
Гипотезу Н0 отклоняют на уровне значимости α, если значение zВ статистики Z, удовлетворяет неравенству zВ < uα (zВ > u1–α) при односторонней альтернативной гипотезе Н1 и |zВ| > u1–α/2 при двухсторонней альтернативной гипотезе Н1.

Для проверки гипотезы Н0 о принадлежности независимых выборок (объемов
n1, n2, …, nk) однородным генеральным совокупностям используют однофакторный дисперсионный анализ Kruskal-Wallis (Kruskal-Wallis ANOVA) и медианный критерий (median test).

Н статистику критерия Kruskal-Wallis вычисляют по формуле:

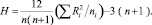
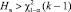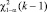Гипотезу Н0 отклоняют на уровне значимости α, когда выборочное значение Нв статистики Н удовлетворяет условию: , где  – квантиль распределения χ2 порядка 1 – α с k – 1 степенями свободы.

Мedian test используют для проверки гипотезы Н0 о том, что все k выборок получены из генеральных совокупностей, имеющих равные медианы, при этом применяют статистику χ2 по формуле:

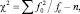
где f0 – наблюдаемые частоты; fe – ожидаемые частоты при условии, что гипотеза Н0 верна. Гипотезу Н0 отклоняют, если 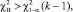, где 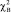 – выборочное значение статистики χ2, при том, что  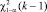– квантиль распределения порядка 1 – α.

Проверка гипотез о принадлежности связанных выборок однородным генеральным совокупностям

Для проверки гипотезы Н0 о принадлежности двух связанных выборок (объемов n)
однородным генеральным совокупностям обычно применяют критерий Wilcoxon (Wilcoxon watched pairs test).

При значительном числе наблюдений (n > 25), для расчета Wilcoxon используют Z статистику:

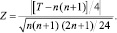
Гипотезу Н0 отклоняют на уровне значимости α, если zВ > u1–α/2, где zВ – выборочное значение статистики Z, u1–α/2 – квантиль нормального распределения N(0, 1) порядка 1 – α/2.

Для проверки гипотезы Н0 о принадлежности k связанных выборок (объемов n) однородным генеральным совокупностям применяют двухфакторный анализ Friedman (Friedman ANOVA) и коэффициент конкордации Kendall (Kendall’s concordance).

Двухфакторный анализ Friedman выполняют с помощью F статистики:

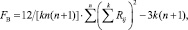
где Rij – ранг j-го объекта, присваиваемый i-м экспертом. Гипотезу Н0 отклоняют на уровне
значимости α, если 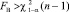, где 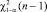 – квантиль распределения χ2 (n – 1)
порядка 1 – α. В качестве меры согласия различных ранжировок n объектов применяли коэффициент конкордации Kendall:

W = F/[k (n – 1)].

Проверка гипотез о некоррелированности признаков

Для проверки гипотезы Н0 о некоррелированности двух признаков (X, Y) измеренных в порядковых или количественных шкалах из пар наблюдений (xi, yi, i = 1, 2, …, n) в качестве мер статистической зависимости употребляют ранговые коэффициенты корреляции Spearman (ρs) и Kendall (τ).

Выборочный коэффициент ранговой корреляции Spearman вычисляют по формуле:

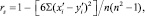
где ,  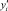– ранги переменных; n – число наблюдений. Коэффициент ранговой корреляции Spearman определяют как модуль выборочного коэффициента: ρs = |rs|. Гипотезу Н0 принимают на уровне значимости α, если rs > 0 и ρs < ρ(α, n), при альтернативной гипотезе Н1, что ρs > 0.

Коэффициент ранговой корреляции Kendall вычисляют по формуле:

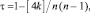
где k – число инверсий в ряду рангов второй переменной 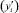при условии, что ранги первой переменной 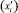упорядочены; n – число наблюдений. При n > 10 для вычисления коэффициента ранговой корреляции Kendall используют Z статистику:

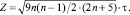
Проверка гипотез о независимости переменных

Для проверки гипотезы Н0 о независимости измеряемых в номинальной шкале двух случайных переменных вида [X, Y] используют точный двухсторонний критерий Fisher (Fisher exact p) и критерий сопряженности χ2.

Критерий Fisher, если объем наблюдений в выборке не превышает 30, вычисляют по формуле:

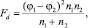
где j1 и j2 – значения углов j в радианах, соответствующие сравниваемым показателям; n1 и n2 – объемы сравниваемых выборок. В прочих случаях выполняют анализ таблиц сопряженности χ2 по формуле:

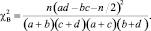
Гипотезу Н0 принимают на уровне значимости α, если 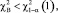, где 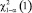 – квантиль распределения χ2 с одной степенью свободы порядка 1 – α. Средний коэффициент сопряженности (φ2) выражают в виде

.

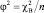Проверка гипотез об эффектах воздействия

Для проверки гипотезы Н0 об отсутствии эффекта воздействия двух связанных выборок (объемов n), для измеряемых в номинальной шкале переменных вида [X, Y] чаще всего используют критерий McNemar, а для переменных вида [X1, X2, ..., Xk] – критерий Cochran (Cochran Q-test).

Для расчета критерия McNemar с объемом выборки, превышающим 50 наблюдений, используют χ2 статистику:

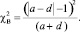
Гипотезу Н0 отклоняют на уровне значимости α, если 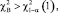, где 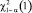 – квантиль распределения χ2 с одной степенью свободы порядка 1 – α.

Комплекс воздействий на объект исследования оценивают с помощью Q критерия Cochran по формуле:

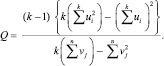
Гипотезу Н0 отклоняют на уровне значимости α, если 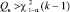, где Qв – выборочное значение Q, а  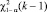– квантиль распределения χ2(k – 1).

Представление результатов статистического исследования

Количественный материал традиционно представляют в виде графиков и таблиц. Во всех случаях при сравнении выборок предпочтение отдаётся наиболее чувствительному из перечня критериев.

Средние выборочные значения количественных признаков обычно приводят в тексте в виде M ± SE, где M – среднее выборочное, SE – стандартная ошибка среднего, или как медиана ± среднее квартильное отклонение (Me ± Q).

Q = 1/2(Q1 – Me) + (Me – Q2),

где Q1 – верхний квартиль, Q2 – нижний квартиль.

В тех случаях, когда анализируемый материал представлен как медиана, указывают верхний и нижний квартили (Q1 – Me – Q2). При ненормальном распределении значений указывают медиану (V0,5), 25-процентиль (V0,25) и 75-процентиль (V0,75).

Разумеется, на этом статистические методы обработки результатов клинических исследований не исчерпываются, однако перечисленные можно смело отнести к наиболее применяемым.