Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРОГРАММНОЕ И АЛГОРИТМИЧЕСКОЕ ОБЕСПЕЧЕНИЯ АППАРАТНЫХ КОМПЛЕКСОВ ПОВЫШЕНИЯ КАЧЕСТВА ПИТАЮЩЕЙ ЭЛЕКТРОЭНЕРГИИ В РАСПРЕДЕЛИТЕЛЬНЫХ СЕТЯХ

Горева Т. С., Портнягин Н. Н.,

2.4. Вейвлет Добеши с компактным носителем

Вейвлеты Добеши имеют носители минимального размера для любого заданного числа нулевых моментов p [75, 100].

Если ψ – вейвлет с р нулевыми моментами, который порождает ортонормированный базис L2(R), то он имеет носитель, размера большего или равного 2р – 1. Вейвлет Добеши имеет носитель наименьшего размера, равный [p + 1, p]. Носитель соответствующий масштабирующей функции φ есть [0,2p – 1].

Если носитель h и φ есть [N1, N2], то носитель ψ есть [(N1 – N2 + 1)/2,
(N2 – N1 + 1)/2].

Когда р = 1, мы получаем вейвлет Хаара. Графики φ и ψ при р = 2,3,4 представлены на рис. 2.5.

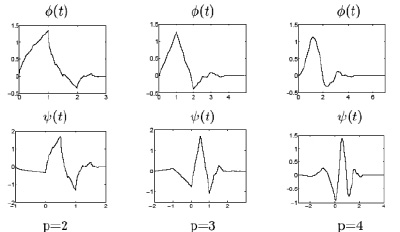
Рис. 2.5. Масштабирующая функция Добеши φ и ψ с р нулевыми моментами

Гладкость φ и ψ одинакова, так как ψ(t) есть конечная линейная комбинация φ(2t – n) [75, 100].