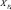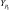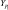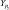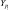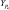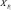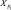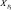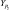Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ЭНЕРГОЭФФЕКТИВНЫЕ СИСТЕМЫ ГИДРАВЛИЧЕСКИХ ПРИВОДОВ ШАГАЮЩИХ МАШИН: МОНОГРАФИЯ
Семенов С. Е., Щербачев П. В., Тарасов О. И.,
Описание электрической части системы
Уравнения, описывающие электродвигатель, а также значения параметров содержатся в [42].
Ток в обмотках электродвигателя вычисляется с учетом активного сопротивления, индуктивности обмоток и противо-ЭДС.
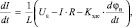
|
где I – |
ток в обмотках электродвигателя; |
|
R – |
активное сопротивление обмоток электродвигателя; |
|
Kэдс – |
коэффициент противо-ЭДС; |
|
L – |
индуктивность обмоток электродвигателя; |
|
Uε – |
напряжение, соответствующее сигналу рассогласования. |
Момент, развиваемый электродвигателем:
Mэ = Kм∙I,
где Kм – коэффициент, связывающий момент и ток.
Для корректировки динамических свойств системы применен ПИД-регулятор. Вычисление напряжения рассогласования Uε производится следующим образом:
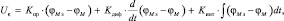
|
где Kпр, Kдиф, Kинт – |
коэффициенты настройки регулятора; |
|
φМз – |
заданный угол поворота выходного звена, соединенного с валом гидродвигателя. |
В модели учтен факт ограничения напряжения источника питания:
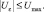
Численные значения величин, описанных выше, приведены в табл. 4.
Таблица 4
Численые значения параметров математической модели
|
Параметр |
Значение |
Размерность |
|
E |
1,5∙109 |
Па |
|
Va |
1∙10–5 |
м3 |
|
Vb |
1∙10–5 |
м3 |
|
Kун |
5∙10–14 |
(м3/с)/Па |
|
Kум1 |
1,27∙10–12 |
(м3/с)/(Па∙рад) |
|
Kум2 |
1,27∙10–12 |
(м3/с)/(Па∙рад) |
|
Kпм |
2,18∙10–12 |
(м3/с)/Па |
|
Kпн |
5∙10–14 |
(м3/с)/Па |
|
Kп |
1∙10–5 |
(м3/с)/Па |
|
V0н |
8∙10–7 |
м3 |
|
V0м |
5,5∙10–6 |
м3 |
|
Kв.тр |
8,77∙10–5 |
(Н∙м)/(рад/с) |
|
J |
1,0∙10–4 |
кг∙м2 |
|
Mтр.э |
1,6∙10–2 |
Н∙м |
|
M |
1,0 |
Н∙м |
|
R |
1,37 |
Ом |
|
Kэдс |
6,4∙10–2 |
В/(рад/с) |
|
L |
1,62∙10–4 |
Гн |
|
Kм |
6,07∙10–2 |
(Н∙м)/A |
|
Kпр |
632 |
В/рад |
|
Kдиф |
–2,19 |
В/(рад/с) |
|
Kинт |
277 |
В/(рад/с) |
В ходе проведения численного эксперимента входным сигналом системы был желаемый угол поворота выходного вала гидродвигателя. Его максимальная величина 45°. Для анализа влияния формы фронта было рассмотрено два вида сигнала: кусочно-линейный и синусоидальный. Вид входных сигналов показан на рис. 31.
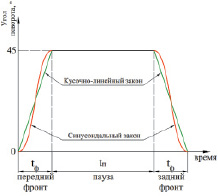
Рис. 31. Входные сигналы
Во время паузы привод отключен, поэтому его можно в расчетах не учитывать. Тогда закон можно сформировать только из переднего и заднего фронта с периодом T = 2tф. По результатам моделирования получены зависимости энергии, затраченной на один цикл поворота выходного звена на 45° и обратно за время T = 2tф. Графики зависимостей показаны на рис. 32.
Параллельно с численным экспериментом проводился физический. Для физического эксперимента был изготовлен опытный образец привода. На выходное звено был установлен дисковый тормоз, который создавал нагрузку на привод. В ходе эксперимента фиксировались следующие параметры: напряжение питания двигателя, потребляемый двигателем ток, задающий сигнал, сигнал с датчика углового положения гидромотора, нагрузка, развиваемая приводом. Вышеперечисленные данные сохранялись и выводились на график (рис. 33). Далее по результатам экспериментов было произведено вычисление количества энергии, затраченного на один цикл для сигналов синусоидальной формы с различными периодами и при различной нагрузке (рис. 34). Форма задающего сигнала – синусоида.
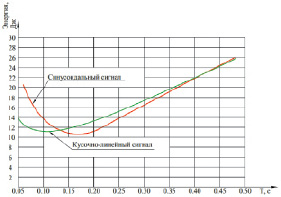
Рис. 32. Влияние формы сигнала на затраты энергии
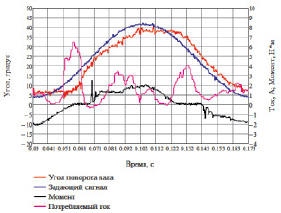
Рис. 33. Результаты физического эксперимента
На рис. 34 показаны экспериментальные данные по величинам потребления энергии приводом в зависимости от нагрузки на выходной вал гидропередачи, и от частоты задающего сигнала. Форма задающего сигнала – синусоида.
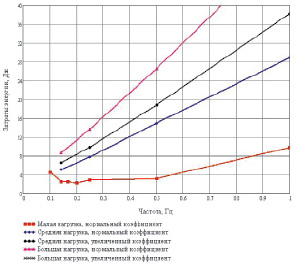
Рис. 34. Экспериментальные данные
по величинам потребления энергии приводом
На рис. 35 представлены экспериментальные данные по величинам потребления энергии приводом в зависимости от частоты задающего сигнала. Форма задающего сигнала – синусоида. Синяя линия показывает – результат математического моделирования под внешней нагрузкой 1 Н∙м. Красными точками обозначен эксперимент, в котором вместо гидромотора используется дросселирующий клапан, имитирующий нагрузку. Зеленой линией обозначен результат эксперимента опытного образца привода при нагрузке, равной нагрузке в математической модели. Розовая линия показывает затраты энергии при работе привода без внешней нагрузки.
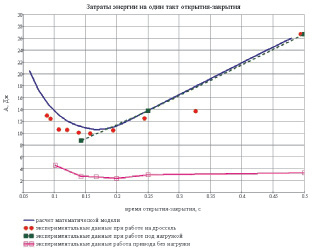
Рис. 35. Экспериментальные данные по величинам потребления энергии
Анализируя полученные результаты, можно сделать некоторые полезные для практического применения выводы:
1. Существует оптимальный с точки зрения затрат энергии закон движения выходного звена. Этот закон определяется временем выхода на заданный угол и формой фронта управляющего сигнала. При одном и той же фронте можно ограничиться оптимальным временем Топт выхода в заданное положение. Если осуществлять движение быстрее, чем за время Топт, то затраты энергии будут главным образом определяться разгоном движущихся масс. Если осуществлять движение дольше, чем за время Топт, то затраты энергии будут определяться диссипативными факторами (такими как трение, утечка жидкости), а разгонные процессы к этому моменту уже завершатся.
2. В каждом конкретном случае применения электрогидравлического привода необходимо отдельно рассматривать влияние внешних нагрузок и формы фронта управляющего сигнала на время Топт. Судя по полученным результатам, учет этого факта может до двух раз повысить энергоэффективность привода.
3. В случае, когда исполнительный механизм не должен следовать некоторой строго заданной траектории с точки зрения технологического процесса, эту траекторию можно синтезировать с точки зрения минимума затрат энергии.
Выше уже было показано, что величина затрат энергии на движение выходного звена привода зависит от траектории движения. Для получения формы оптимальной траектории следует разработать методику ее направленного поиска.
Поворот выходного вала из начального положения на некоторый заданный угол φз за время T может быть осуществлен по разным траекториям, что проиллюстрировано на рис. 36.
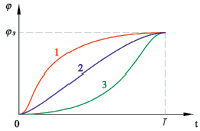
Рис. 36. Примеры траекторий
Для реализации каждой траектории, как рассматривалось выше будет затрачено свое количество энергии. В связи с этим можно предположить, что существует оптимальная с точки зрения затрат энергии траектория. Для поиска такой траектории ее необходимо
задать в общем виде некоторым набором параметров и, используя математическую модель провести процедуру минимизации по энергетическому критерию.
В случае периодического движения задавать траекторию можно при помощи разложения желаемой кривой в ряд Фурье, как это сделано в работе [44]. При задании монотонно возрастающей кривой на определенном промежутке в рассматриваемой задаче более удобно использовать параметрические кривые B-сплайны. В работах [45 и 46] такие кривые использованы для синтеза траекторий звеньев манипуляторов.
B-сплайн – это параметризированная кривая, которая задается набором управляющих точек (полюсов) и узлов. Описывается она следующим уравнением:
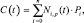
|
где p = m – n – 1 – |
степень B-сплайна; |
|
Pi – |
полюсная точка; |
|
Ni,p(t) – |
базисная функция; |
|
t – |
параметр, меняющийся в пределах от 0 до 1. |
Базисные функции вычисляются по следующим выражениям:
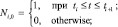
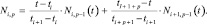
Графическая интерпретация траектории, заданной вышеприведенными зависимостями, показана на рис. 37. Данная кривая является B-сплайном 4-го порядка с пятью управляющими точками.
Кроме того, на рис. 37 показаны ограничения, наложенные на перемещения управляющих точек. Точки P0 и P4 зафиксированы для задания начального и конечного положений. Скольжение точек P1 и P3 вдоль прямой φ = φmax обеспечивает касательность траектории к прямым φ = 0 и φ = φmax в начальной и конечной точках соответственно. Целесообразно ввести декартову систему координат,
ось абсцисс которой будет совпадать с осью времени в данном случае, а ось ординат – с осью угла. Значения координат управляющих точек в выбранной системе и наложенные ограничения приведены в табл. 5.
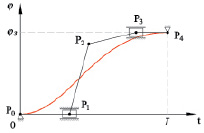
Рис. 37. Траектория, заданная B-сплайном
Таблица 5
Координаты точек
|
Координата |
Значение |
Ограничения |
Примечание |
|
|
0 |
= 0 |
начальная точка |
|
|
var |
≥ 0,05T |
варьируемый параметр |
|
|
var |
варьируемый параметр |
|
|
|
var |
≤ 0,1T |
варьируемый параметр |
|
|
T |
= T |
конечная точка |
|
|
0 |
= 0 |
начальная точка |
|
|
0 |
= 0 |
зафиксирована на φ = 0 |
|
|
var |
варьируемый параметр |
|
|
|
φmax |
= φmax |
зафиксирована на φ = φmax |
|
|
φmax |
= φmax |
конечная точка |
Таким образом, в оптимизационной задаче будет четыре варьируемых параметра.
Целью работы является минимизация затрат энергии при работе привода. Поэтому минимизируемый критерий можно записать следующим образом:
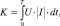
|
где U – |
напряжение источника питания привода; |
|
I – |
потребляемый приводом ток. |
В качестве первого приближения выбраны значение координат точек, приведенные в табл. 6.
Таблица 6
Значения параметров для первого приближения
|
Координата |
|
|
|
|
|
Значение |
0,25∙T |
0,5∙T |
0,75∙T |
0,5∙φmax |
Соответствующая этим значением форма кривой при T = 0,01с и φmax = π/4, а также отработка этой траектории приводом показаны на рис. 38.
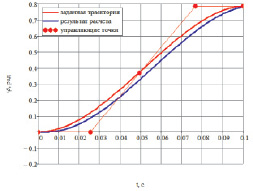
Рис. 38. Траектория первого приближения
Для проведения процедуры поиска минимума выбранного критерия использован метод Нелдера – Мида, известный так же как метод «деформируемого многогранника».
Была проведена серия численных экспериментов, в ходе которой изучалось влияние нагружающего момента и присоединенного момента инерции на форму оптимальной траектории. Выбранные значения нагружающего момента, момента инерции и расчетные затраты энергии приведены в табл. 7.
Таблица 7
Расчетные точки и результаты
|
Момент инерции |
Нагружающий момент |
Затраты энергии |
|
1 кг∙см2 (Jном) |
0,0 Н∙м |
1,37 Дж |
|
0,2 Н∙м |
1,71 Дж |
|
|
1,0 Н∙м |
3,88 Дж |
|
|
5,0 Н∙м |
16,62 Дж |
|
|
5 кг∙см2 (5∙Jном) |
0,0 Н∙м |
1,51 Дж |
|
0,2 Н∙м |
1,77 Дж |
|
|
1,0 Н∙м |
3,88 Дж |
|
|
2,0 Н∙м |
7,05 Дж |
|
|
25 кг∙см2 (25∙Jном) |
0,0 Н∙м |
2,60 Дж |
|
0,2 Н∙м |
2,67 Дж |
|
|
1,0 Н∙м |
4,51 Дж |
|
|
2,0 Н∙м |
7,22 Дж |
На рис. 39 приведены результаты расчета оптимальных траекторий для момента инерции 1 кг∙см2.
На рис. 40 приведены результаты расчета оптимальных траекторий для момента инерции 5 кг∙см2.
На рис. 41 приведены результаты расчета оптимальных траекторий для момента инерции 25 кг∙см2.
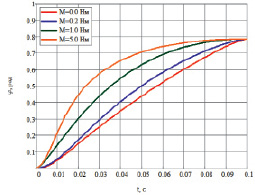
Рис. 39. Результаты расчета для J = 1 кг∙см2
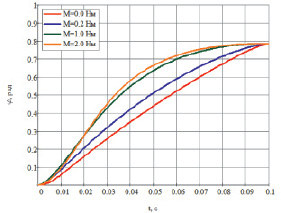
Рис. 40. Результаты расчета для J = 5 кг∙см2
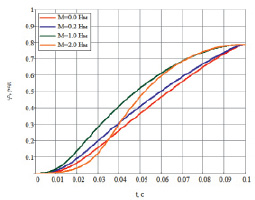
Рис. 41. Результаты расчета для J = 25 кг∙см2
Анализируя полученные результаты, можно сделать ряд выводов:
Форма оптимальной с точки зрения затрат энергии траектории зависит от ряда параметров. Определяющие среди них – нагружающий момент и момент инерции нагрузки. Все результаты даны для времени процесса T = 0,01 с, но оптимизацию следует проводить отдельно для каждого требуемого времени.
Как видно из табл. 7 при малых нагружающих моментах рост затрат энергии не пропорционален увеличению самого момента, из чего можно сделать вывод, что в этом случае они в большей степени определяются инерционной нагрузкой.
В некоторых случаях точность позиционирования и жесткость привода выходят на первый план по сравнению с энергоэффективностью. Особенно, если шагающая машина не является автономной. В этом случае стоит обратить внимание на дроссельный привод.