Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭМПИРИЧЕСКАЯ ТЕОРИЯ ВСЕЛЕННОЙ

Курков А. А.,

3.5. Осциллятор солнечной системы, решение квантовой системы

В квантовой механике существует понятие осциллятор. Теперь покажем, что планетная система образует связанную систему маятников (осциллятор). Критерием устойчивости планетных орбит и планетной системы в целом служит условие кратности периода обращения планеты к периоду встреч 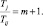[10]:

(10)

Здесь m = 1, 2, ... – целое положительное число.

Для планет с периодами обращения Ti и Tj (при Ti < Tj) период встречи Tij равен:

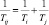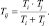или (11)

Подставляя уравнение (11) в (10), получим уравнение осциллятора:

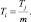(12)

В качестве Tj выберем период обращения Солнца вокруг центра масс системы Tj = Tc и вычислим 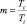(табл. 5). Здесь Ti уже период обращения планет-гигантов.

Таблица 5

Осциллятор Солнечной системы

Объект	Солнце	Юпитер	Сатурн	Уран	Нептун	Плутон
Ti, лет	179,77	11,86	29,45	84,01	164,8	247,7
Tij, лет	–	11,12	25,29	57,15	85,75	103,8
m	–	15,07	6,07	2,13	1,09	0,72

Астрономы уже не относят Плутон к планетам, что подтверждается не только физическими характеристиками планеты, но и дробным значением числа осциллятора 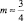. Дробные значения m показывают, что объект находится на траектории «резонанса». Для остальных планет условие устойчивости выполняется достаточно точно.

В табл. 5 величина m пробегает значения не по порядку, что даёт основания предполагать конечное количество уровней в системе:

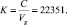
Из этого количества уровней системы планеты Нептун и Уран представлены одним уровнем осциллятора каждая (табл. 5 значение m), а количество уровней Сатурна, Юпитера и Солнца определяется количеством уровней осциллятора над каждой ямой суперпозиции гравитационных волн Солнца.

Рассмотрим графический аналог решения уравнения Э. Шредингера для Солнечной системы на рис. 5 по результатам разложения потенциала Солнца на структурные коэффициенты k и на основании данных табл. 5. Для этого разложим гравитационный потенциал Солнца на суперпозицию гравитационных волн и наложим на него осциллятор, полученный выше.

Длина периода основной гравитационной волны Солнца равна:

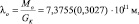
период волны:

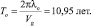
На рис. 5 гравитационный потенциал Солнца представлен суммой двух волн (имеет два энергетических состояния). Основная волна имеет длину периода ?o и одну планету в этом состоянии (Юпитер). Вторая волна имеет период длиной 2*?o и три состояния на этом энергетическом уровне (Сатурн, Уран, Нептун) по количеству проекций «спина».

Разложение гравитационного потенциала Солнца по энергетическим состояниям системы демонстрирует рис. 5.

Поскольку все уровни осциллятора тождественны, то массы планет-гигантов и Солнца определяются количеством уровней осциллятора над ямой каждой из планет в суперпозиции гравитационных волн Солнца. Масса одного уровня осциллятора Солнечной системы Ml равна:

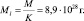
Здесь M – масса Солнечной системы, которая с высокой точностью равна массе Солнца M ? Mo = 1,99*1033 г.

На рис. 5 сверху показан осциллятор, внизу суперпозиция гравитационных волн. Вертикальные пунктирные линии выделяют «ямы» и количество уровней объектов. Сноски указывают название объекта (планету). Чтобы наложить полученный осциллятор на суперпозицию волн время пересчитывается в расстояние по закону Кеплера. В табл. 6 приведены результаты расчета масс планет-гигантов.

Рис. 5. Квантовые состояния Солнечной системы

Выполненные расчеты показывают, что Солнечная система обладает определенной иерархией структуры. По этой причине истинными спутниками Солнца являются планеты – гиганты, так как их массы кратны массе уровня в соответствие с табл. 6:

- масса Юпитера равна 22*Ml;

- Сатурна – 6*Ml;

- Урана и Нептуна – по одному уровню Ml.

Отклонения расчетных масс планет от наблюдаемых масс довольно высоки. Для проверки адекватности выполненных расчетов в нижней строке табл. 6 приведены наблюдаемые и расчетные суммы масс всех планет-гигантов. Отклонение расчетной суммы масс от наблюдаемой суммы масс, в этом случае, не превышает 0,5 %. Из этого следует, что расчеты выполнены адекватно, но в них не учтены некоторые детали второго порядка малости (например, «спин»).

Таблица 6

Результаты вычислений масс планет-гигантов

Планета	Масса, кг		Ошибка расчета, %	Количество уровней
	Наблюдаемая	Расчётная
Солнце	1,99*1030	–		22321
Юпитер	1,90*1027	1,96*1027	3,1	22
Сатурн	5,68*1026	5,34*1026	–6,4	6
Уран	8,7*1025	8,91*1025	2,4	1
Нептун	10,3*1025	8,91*1025	–15,6	1
Планеты	265,8*1025	267,1*1025	0,487	30

Выше говорилось об иерархии структуры Солнечной системы и о том, что планеты земной группы находятся в области интерференции основной гравитационной волны Солнца. Благодаря интерференции сумма масс всех планет земной группы должна быть меньше массы одного уровня системы Ml.

Спутники планет-гигантов подчиняются тем же правилам иерархии, которым подчиняются они сами при расположении вокруг Солнца (по орбитам и массам), то есть сумма масс спутников планеты не должна превышать 30 масс ее уровня:

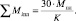
Однако расчёт их орбит и масс усложняется из-за интерференции гравитационных волн, из-за сохранения момента движения и проблем учета «спина».

В соответствие с правилом для спутников планет-гигантов, массы спутников (истинных спутников) планет земной группы будут меньше возможно допустимой массы для космического тела, поэтому истинных спутников у планет земной группы нет. Другая причина состоит в малой длине их основной волны по сравнению с радиусом самой планеты. Те спутники, которые наблюдаются у планет земной группы, имеют такую же природу, что и сами планеты из-за интерференции гравитационных волн. Поскольку планета Марс существует в поясе астероидов, то он сам больше похож на астероид, а его спутники – тем более. По этой же причине Луна похожа на Землю. Законы сохранения момента движения и проблема «спина» по-видимому, являются причиной разницы в массах Земли и Луны, но это пока предположение. По-видимому, порядок интерференции определяет количество спутников: у Марса – 2 спутника; у Земли – 1; у Венеры и Меркурия спутников нет.