
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ
Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,
1.1. История математики как история развития представлений о специфике математического эксперимента
Многие математические результаты, как на заре развития математики, так и на протяжении всей истории ее развития, вплоть до сегодняшних дней были получены посредством экспериментов и индуктивных рассуждений, лишь позднее они были доказаны дедуктивно. Правда, прямых свидетельств этому мало. Во все времена ученые не любят рассказывать о процессе своего творчества, показывать, как создавались те или иные математические теории, путем каких догадок, проверок, отбраковки ошибочных догадок приходили они к своим выводам. Публикуются только конечные результаты. Среди математиков, наверное, только Л. Эйлер писал о процессе своего творчества. Этим и уникальны его работы.
Рассмотрим более подробно как на основе экспериментов, наблюдений, догадок формулировались математические результаты, и начнем с древности.
1.1.1. Древность. Натурные эксперименты в математике
Математические знания существовали во многих древних землевладельческих государствах, однако восстановить уровень знаний, который в них существовал, можно лишь по сохранившимся документам, найденным при археологических раскопках. Далеко не всегда документы сохранялись, и поэтому сколько-нибудь подробные данные мы имеем лишь о математике Древнего Египта и Древнего Вавилона. Вавилоняне умели правильно вычислять площади прямоугольников, треугольников, трапеций, объемы куба, параллелепипеда, призмы, пирамиды. Однако мы не найдем у них самого привычного нам элемента математики – доказательства. Правила вычисления, по всей видимости, возникали как эмпирические соотношения в результате многочисленных измерений, затем заучивались как догма и передавались от одного поколения писцов к другому. Порукой истинности утверждений также служила вековая практика их использования. При этом не разделялись точные и приближенные формулы, при этом приближенная формула должна была удовлетворять практическим требованиям.
Характерным примером служит использовавшееся еще в древнем Египте правило для вычисления площади произвольного четырехугольника со сторонами a, b, c, d. Египтяне считали, что площадь четырехугольника равна произведению полусумм пар противоположных сторон, то есть
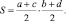
Эта формула дает точные результаты лишь для прямоугольников, в остальных случаях результат приближенный, и можно привести примеры четырехугольников, для которых ее погрешность сколь угодно велика. Так, например, площадь ромба с острым углом. Чем меньше острый угол, тем больше погрешность. Однако на практике эта формула применялась в Египте для расчета площади земельных участков, форма которых обычно была близка к прямоугольнику, а в этом случае формула давала достаточную точность. Сознавали ли древние землемеры, что формула является приближенной, этого мы не знаем.
На основе натурных экспериментов египетским математикам удалось решить и другую, гораздо более трудную задачу. Они нашли способ, хоть и приближенный, вычисления площади круга по поперечнику (диаметру): по их правилам площадь круга считалась равной площади такого квадрата, сторона которого есть  поперечника круга. В данном случае п ? 3,16. Правило было получено, скорее всего, эмпирически. Его происхождение пытались объяснить по-разному, но почти все гипотезы неубедительны. Одна из наиболее правдоподобных гипотез описана в книге А.Е. Раик [73].
поперечника круга. В данном случае п ? 3,16. Правило было получено, скорее всего, эмпирически. Его происхождение пытались объяснить по-разному, но почти все гипотезы неубедительны. Одна из наиболее правдоподобных гипотез описана в книге А.Е. Раик [73].
Сначала впишем круг в квадрат со стороной 1. Вырежем из этого квадрата четыре квадратика со стороной  . Площадь оставшейся части равна
. Площадь оставшейся части равна 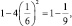 но она еще явно больше площади круга. Вырежем еще восемь квадратиков со стороной
но она еще явно больше площади круга. Вырежем еще восемь квадратиков со стороной  . Их площадь равна
. Их площадь равна 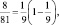 а площадь оставшейся части равна
а площадь оставшейся части равна 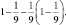
Возможно, что египтяне поступали именно так, и решили, что площадь оставшейся части равна площади круга [72, с. 14].
В Древнем Вавилоне площадь круга находилась по формуле 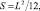 где S – площадь круга; L – длина окружности. Логика рассуждений ученых, приведшая к получению этой формулы, пока не воссоздана.
где S – площадь круга; L – длина окружности. Логика рассуждений ученых, приведшая к получению этой формулы, пока не воссоздана.
Самое удивительное, что египтяне и вавилоняне умели находить объем пирамиды, а египтяне даже объем усеченной пирамиды с квадратными основаниями. Точный вывод формул требует знаний, которыми египтяне и вавилоняне наверняка не обладали, поскольку для нахождения объема усеченной пирамиды требовалось применение предельного перехода.
Объем пирамиды, вообще говоря, нельзя найти путем разрезания куба. Это можно сделать лишь для некоторых пирамид. Например, в вавилонских глиняных табличках вычисляется лишь объем пирамиды, угол между основанием (квадратным) и боковыми гранями которой равен 45°, а куб можно разрезать на шесть таких пирамид, взяв в качестве их общей вершины центр куба, а в качестве оснований – его грани. Так поступали при нахождении правила для вычисления объема пирамиды и египтяне. И хотя этот вывод годится не для всех пирамид, египтяне спокойно пользовались этим правилом для любой пирамиды [72].
1.1.2. Древняя Греция. Мысленный эксперимент в форме механических интерпретаций
Важный шаг в развитии научных представлений об экспериментальных методах в математики был сделан Архимедом. Им были найдены площади круга и параболических сегментов, объемы шара, эллипсоида, сегментов шара. В сочинениях Архимеда все найденные им зависимости для площадей и объемов доказываются строго геометрически, Например, методом исчерпывания, по Евдоксу доказывается, что разность между объемом шара и величиной 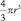 может быть сделана сколь угодно малой, но откуда берется сама величина
может быть сделана сколь угодно малой, но откуда берется сама величина 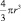 – не поясняется. И поскольку Архимед нашел не только объем шара, но и объемы многих других тел (а также площади целого ряда фигур), то ясно, что Архимед владел способом, позволяющим находить (а не только доказывать) формулы для площадей и объемов. Но в чем состоял этот способ, долгое время оставалось неясным. И лишь в 20 веке (1908 год) была найдена рукопись Архимеда «Послание к Эратосфену». Это была работа о механическом
– не поясняется. И поскольку Архимед нашел не только объем шара, но и объемы многих других тел (а также площади целого ряда фигур), то ясно, что Архимед владел способом, позволяющим находить (а не только доказывать) формулы для площадей и объемов. Но в чем состоял этот способ, долгое время оставалось неясным. И лишь в 20 веке (1908 год) была найдена рукопись Архимеда «Послание к Эратосфену». Это была работа о механическом
методе решения геометрических задач. В ней приводятся следующие эвристические рассуждения.
Пусть, например, необходимо вычислить объем шара. Одновременно с шаром строят конус и цилиндр, радиусы оснований и высоты которых, равны диаметру шара (рис. 1). Через все эти тела проводят сечение, параллельное основаниям, на некотором произвольном фиксированном расстоянии от оснований.
АК2 = ОК2 + ОА2 = ОК2 + OL2.
В то же время АК2 = АВ·ОА, что позволяет сделать вывод о том, что
ОК2 + OL2 = АВ·ОА.
Таково же соотношение между величинами, пропорциональными слагаемым
п*АВ2·ОА = п*ОК2·АВ + п*OL2·AB.
Так получается соотношение между горизонтальными сечениями шара, цилиндра и конуса.
Этому соотношению Архимед дает механическую интерпретацию, основанную на правиле рычага, или, что то же самое, двуплечных весов. Другими словами, если принять точку А за точку опоры рычага, то элемент цилиндра, закрепленный в точке О, уравновесит элементы шара и конуса, закрепленные в Т (AT = AB). Переходя к объемам тел как к суммам всех произвольных сечений, параллельных друг другу, он получает
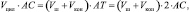
отсюда
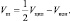
Но так как 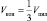 , то
, то
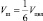 или
или 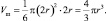
Тот же способ механической аналогии Архимед применил в сочинении «О квадратуре параболы». Параболическая пластинка представляется подвешенной к одному плечу неравноплечного рычага и разделенной на элементы, каждый из которых уравновешен соответствующей нагрузкой на другом плече [76].

Рис. 1. Вычисление объема шара
В соответствии с научной традицией своего времени Архимед переводил доказательства, полученные методом механической аналогии, на общепринятый язык метода исчерпывания с обязательным завершением последнего в каждом отдельном случае доказательством от противного.
Вместе с тем Архимед продолжал широко использовать для получения соотношений и натурные эксперименты. Так, например, он очень ясно и понятно описал, как измерить угловые размеры Солнца [54, с. 23]. Он определил видимый поперечник Солнца, как заключенный между 1/200 и 1/164 долями прямого угла (или между 27 и 35 минутами, в действительности 32 минуты).
«Укрепив длинную линейку на вертикальной подставке, расположенной в месте, откуда виден восход Солнца, поставим на линейку вертикально небольшой точенный цилиндр. Когда Солнце близко к горизонту и на него можно смотреть, линейка поворачивается в сторону Солнца и глаз располагается на краю линейки. При этом цилиндр, находясь между Солнцем и глазом, закрывает все Солнце. Затем постепенно перемещают цилиндр от глаза, пока Солнце не начнет слегка показываться со всех сторон цилиндра; на этом месте цилиндр закрепляется» [55, с. 13–14].
Сходным образом рассуждал и Эратосфен при определении размеров Земли. Эратосфен жил в Александрии в III веке до н.э. Южнее Александрии на берегу Нила лежит город Сиена. В день летнего солнцестояния – самый длинный день года – в Сиене солнце заглядывает на дно самых глубоких колодцев, а в Александрии в этот день дно колодцев остается в тени. Там солнечные лучи падают на Землю не отвесно, как в Сиене, а под углом и освещают только стенку колодца. Эратосфен измерил угол между направлением солнечного луча и стенкой колодца. Оказалось, что этот угол равен 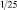 развернутого угла. Вероятно, Эратосфен рассуждал так: солнечные лучи всюду параллельны, а колодцы всегда копают по отвесу. Солнце может по-разному освещать колодцы в Сиене и Александрии только потому, что Земля не плоская. Скорее всего, она круглая, как шар. Но раз угол между Солнечным лучом и отвесом в Александрии равен
развернутого угла. Вероятно, Эратосфен рассуждал так: солнечные лучи всюду параллельны, а колодцы всегда копают по отвесу. Солнце может по-разному освещать колодцы в Сиене и Александрии только потому, что Земля не плоская. Скорее всего, она круглая, как шар. Но раз угол между Солнечным лучом и отвесом в Александрии равен 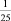 развернутого угла, то расстояние между Александрией и Сиеной в 25 раз меньше длины меридиана, соединяющего полюсы земного шара. Расстояние от Александрии до Сиены было приблизительно известно. Умножив его на 25, Эратосфен определил длину меридиана. Ошибка, сделанная Эратосфеном, была совсем невелика, особенно если учитывать, как неточны были в то время измерения расстояний и углов [39, с. 149.].
развернутого угла, то расстояние между Александрией и Сиеной в 25 раз меньше длины меридиана, соединяющего полюсы земного шара. Расстояние от Александрии до Сиены было приблизительно известно. Умножив его на 25, Эратосфен определил длину меридиана. Ошибка, сделанная Эратосфеном, была совсем невелика, особенно если учитывать, как неточны были в то время измерения расстояний и углов [39, с. 149.].
1.1.3. Численные эксперименты в трудах Пифагорейцев
Пифагорейцы сопоставили три последовательности чисел:
1) натуральный ряд;
2) квадраты чисел натурального ряда;
3) разности последовательных квадратов:
|
1) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
. |
. |
. |
|
2) |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
121 |
144 |
169 |
196 |
. |
. |
. |
|
3) |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
. |
. |
. |
Наблюдение обнаружило следующий факт: когда число третьей последовательности квадратное, то оно в сумме со стоящим над ним квадратным числом даёт квадратное число, стоящее во второй последовательности на следующем справа месте:
9 + 16 = 25; 25 + 144 = 169 или 32 + 42 = 52; 52 + 122 = 132.
Этот факт можно доказать и в общем виде.
Также на основе многочисленных вычислений были изучены свойства некоторых групп натуральных чисел, которые получили название «Треугольники Тартальи».
1) 1 + 2 = 3
4 + 5 + 6 = 7 + 8
9 + 10 + 11 + 12 = 13 + 14 + 15
16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24
. . . . . . . . . . . . . . . . . . . . . . . . . . .
2) 32 + 42 = 52
102 + 112 + 122 = 132 + 142
212 + 222 + 232 + 242 = 252 + 262 + 272
362 + 372 + 382 + 392 + 402 = 412 + 422 + 432 + 442
552 + 562 + 572 + 582 + 592 + 602 = 612 + 622 + 632 + 642 + 652
. . . . . . . . . . . . . . . . . . . . . . . . . . .
3) Существует еще такой «числовой треугольник»:
13 = 1
23 = 3 + 5
33 = 7 + 9 + 11
43 = 13 + 15 + 17 + 19
53 = 21 + 23 + 25 + 27 + 29
. . . . . . . . . . . . . . . . . . [38, с. 182–183].
1.1.4. Математика в Западной Европе к XVI–XVII векам. Рождение методологии прикладной математики
Ученые Западной Европы XVI–XVII веков – это, прежде всего, инженеры, изобретатели, астрономы, философы. К математическим задачам их толкала потребность решить встававшие перед ними практические проблемы, которые они решали в тесном контакте с мастерами и ремесленниками того времени. Решение практических задач открывало новые математические объекты, которые становились предметом дальнейшего изучения, в свою очередь, стимулируя теоретическую мысль.
Рассмотрим характерный пример, связанный с работами Христиана Гюйгенса (1629–1695). Началом послужила одна из важнейших практических задач XVII века – усовершенствование маятниковых часов. Было подмечено, что период колебаний простого кругового маятника зависит от размаха и не позволяет ему быть точным измерителем времени. А между тем, именно в это время точные часы были очень нужны,
прежде всего, для целей навигации. Широту в XVII веке уже умели определять довольно точно, измеряя высоту над горизонтом небесных светил. Теоретически долготу любого места в ходе плавания можно определять путем сравнения местного времени, определяемого по кульминации Солнца или звезд, со временем пункта отправления, если только это время достаточно точно хранят хорошие часы. В качество часов долгое время все и упиралось: обычные маятниковые часы, в которых центр тяжести маятника движется по окружности, нужной точности не обеспечивали, особенно в условиях качки корабля. Лучше других это понимал Христиан Гюйгенс, соединивший в своем лице талант изобретателя, выдающегося часового мастера с талантом математика. Гюйгенс предположил и разработал несколько остроумных конструкций маятниковых часов, повышающих точность, и он же заметил, что главным препятствием к дальнейшему увеличению точности служит принципиальное свойство обычного маятника – зависимость периода колебаний от их амплитуды. На качающемся корабле не удавалось сохранить постоянную амплитуду колебаний, и часы неизбежно теряли точность. Гюйгенс поставил интереснейшую задачу: «По какой кривой (вместо окружности) должен двигаться центр тяжести маятника для того, чтобы период колебаний не зависел от амплитуды?» Гюйгенс нашел эту кривую с помощью удивительно остроумных рассуждений, приведенных в его трактате «Маятниковые часы», опубликованном в 1673 году. Искомая кривая оказалась циклоидой – кривой, которую описывает закрепленная точка окружности, катящаяся по прямой без скольжения. Заметим, что Гюйгенс весьма живо и остроумно определял циклоиду: это та кривая, «которую описывает в воздухе гвоздь, вбитый в обод колеса, при его качении». Как раз незадолго до этого, в работах учеников Галилея Вивиани и Торричелли эта кривая была впервые описана, название «циклоида» было придумано самим Галилеем. Однако, как заставить центр тяжести маятника двигаться точно по циклоиде? Гюйгенс нашел оригинальное решение: Пусть нить подвеса маятника колеблется между двух «щек», изогнутых по кривым – эволютам циклоиды. Для того, чтобы правильно изогнуть «щеки», нужно было найти эти кривые – эволюты циклоиды. Гюйгенс нашел их, создав по пути теорию эволют и эвольвент. Эта теория позволила Гюйгенсу построить часы, в которых центр тяжести маятника двигался по циклоиде, в результате чего период колебаний перестал зависеть от амплитуды. Работа Гюйгенса показала с особенной наглядностью пользу соединения математики и практики, плодотворность применения математических методов и теорем к решению конкретных технических задач [70, с. 45–47].
Метод «неделимых» И. Кеплера. В 1613 году И. Кеплер женился. Когда он покупал вино для свадьбы, он был изумлен тем, как продавец определял вместимость бочки. Продавец брал палку, на которой были нанесены деления, и с ее помощью узнавал расстояние от наливного отверстия до самой дальней точки бочки – края днища. Проделав это одно измерение, он сразу же говорил, сколько литров вина в данной бочке.
Кеплера заинтересовало, насколько точно торговец определил объем бочки при помощи всего одного измерения. Так ученый первым обратил внимание на класс задач, исследование которых привело к созданию интегрального исчисления. Вначале Кеплер нашел формулу для вычисления объема бочки, а затем и других тел вращения (всего для 92 тел вращения), которым он дал названия «лимон», «яблоко», «груша», «айва», «слива», «земляника» и т.п. Для нахождения объемов этих неправильных тел ученый применял метод исчерпывания, разбивая тело на множество элементарных частей и заполняя его фигурами, объемы которых поддавались вычислению.
Так, для нахождения объема тора Кеплер разбил его меридиальными сечениями на бесконечное количество кружков, толщина которых с внешней стороны несколько больше, чем с внутренней. Объем такого кружка равен объему цилиндра с основанием, равным сечению тора, и высотой, равной высоте кружка в его средней части. Отсюда сразу получается, что объем тора равен объему цилиндра, у которого площадь основания равна площади сечения тора, а высота равна длине окружности, которую описывает точка – центр круга, образующего тор [54, с. 63].
1.1.5. Численные эксперименты и вопросы аддитивной арифметики
Аддитивная арифметика – это область арифметики, которая в основном занимается вопросами о представлении целых чисел в виде суммы целых чисел наперед заданного вида. Многие теоремы этой арифметики были сформулированы на основе рассмотрения различных частных случаев.
Проблема Варинга. Еще у Диофанта возникла идея о представлении натуральных чисел суммами квадратов натуральных же чисел, в частности, о представлении суммой не более четырех квадратов. Клод Гаспар Баше (1625) проверил это положение для всех чисел, не превышающих 325. В 1636 году П. Ферма заявляет, что имеет доказательство этой теоремы, но в 1659 году сообщает о трудностях её доказательства. Доказательство теоремы, что всякое натуральное число есть сумма не более четырех квадратов натуральных же чисел, было дано Л. Эйлером в 1751 году и уточнено Ж. Лагранжем в 1772 году с указанием об использовании им идеи доказательства Л. Эйлера. Очень многие математики занимались в дальнейшем родственными этой теореме вопросами (Э. Варинг, Д. Гильберт, И.М. Виноградов, Ю.В. Линник).
Проблема Гольдбаха. Христиан Гольдбах (1690–1764) в 1742 году в письме к Л. Эйлеру о разных недоказанных математических предложениях, которые подтверждаются проверкой, упоминает и о предложении, что всякое число есть сумма трех простых чисел, причисляя к простым числам единицу. Л. Эйлер отвечает: «Предложение о том, что всякое четное число есть сумма двух простых чисел, я считаю настоящей теоремой, хотя я и не в состоянии ее доказать». Л. Эйлер указывает, что если эта теорема доказана, то из нее вытекает, что всякое нечетное число есть сумма трех простых чисел.
Накопился громадный эмпирический материал, подтверждающий высказанное Х. Гольдбахом предположение. С тех пор как Х. Гольдбах выдвинул эту гипотезу, математики не сомневались, что она, как и Великая теорема Ферма, верна. Тем не менее, в отличие от теоремы Ферма, никто никогда не претендовал на то, что сумел ее доказать. К решению этой проблемы существует подход «в лоб» – надолго запустить компьютерную программу, которая бы последовательно проверяла это утверждение на всё больших и больших четных числах. Таким способом можно было бы опровергнуть теорему, будь она неверна. Но невозможно и доказать, поскольку никогда нельзя гарантировать, что очередное число, проверяемое программой, не окажется первым исключением из правила. В действительности мы знаем, что гипотеза Гольдбаха верна, по крайней мере, для всех четных чисел, не превышающих 100 000. В 30-е годы XX века группа русских математиков установила, что существует такое конечное n, что любое четное число может быть представлено в виде суммы не более чем n простых слагаемых, а также что гипотеза Гольдбаха верна для большого класса четных чисел. Однако доказательство теоремы до сих пор не найдено [38, с. 174–175].
1.1.6. Численные эксперименты как основа создания генераторов простых чисел
Простые числа так причудливо расположены в натуральном ряду, что у математиков не было надежды вывести формулу, которая давала бы все такие числа и никакие другие. Поэтому попытались достичь более легкой цели – найти формулу, подставляя в которую вместо n одно за другим натуральные числа, получать каждый раз простое число. Одну из первых таких формул предложил П. Ферма. Она имела вид: 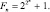 Но в данном случае интуиция подвела ученого. При n = 0, 1, 2, 3, 4 действительно получаются простые числа, но значение n = 5 он не проверял, иначе он обнаружил бы, что число 232 + 1 = 4294967297 делится на 641. Не удались попытки записать желанную формулу и в виде многочлена. Л. Эйлер установил, что многочлен f(n) = n2 – n + 41 принимает простые значения для всех n = 0, 1, 2, …, 40. Но f(41) = 412 – 41 + 41 – составное число. Еще больше простых чисел дает многочлен g(n) = n2 – 79n + 1601 – они получаются при всех целых n от 0 до 79. Но при n = 80 получаем составное число. Неизвестно, бесконечно ли множество простых значений многочленов f(n) и g(n).
Но в данном случае интуиция подвела ученого. При n = 0, 1, 2, 3, 4 действительно получаются простые числа, но значение n = 5 он не проверял, иначе он обнаружил бы, что число 232 + 1 = 4294967297 делится на 641. Не удались попытки записать желанную формулу и в виде многочлена. Л. Эйлер установил, что многочлен f(n) = n2 – n + 41 принимает простые значения для всех n = 0, 1, 2, …, 40. Но f(41) = 412 – 41 + 41 – составное число. Еще больше простых чисел дает многочлен g(n) = n2 – 79n + 1601 – они получаются при всех целых n от 0 до 79. Но при n = 80 получаем составное число. Неизвестно, бесконечно ли множество простых значений многочленов f(n) и g(n).
В дальнейшем попытки отыскать формулу для простых чисел в виде многочленов были оставлены в связи с результатами Л. Эйлера и Х. Гольдбаха [27, с. 33].
1.1.7. Статистические эксперименты в разрешении парадоксов теории вероятностей
Рассказывают, что однажды к Галилею обратился один игрок с просьбой разъяснить ему непонятное явление: почему при бросании трех игральных костей сумма 10 выпадает чаще, чем 9? Это кажется странным, ведь сумма 10, так же как и сумма 9, выпадает в шести комбинациях:
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4;
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3.
Галилей разъяснил этот парадокс в работе «О выходе очков при игре в кости». Оказывается, не все перечисленные комбинации равновозможны. Работа Галилея была опубликована в 1718 году.
До этого Ж. Мере обращался к Б. Паскалю с такими задачами:
– почему при бросании трех костей чаще выпадает сумма, равная 11, чем 12?
– подтвердить наблюдение, что вероятность выпадения хотя бы одной шестерки при четырех бросаниях игральной кости больше 1/2;
– сколько раз надо подбросить две игральные кости, чтобы число случаев, благоприятствующих выпадению хотя бы однажды двух шестерок сразу, было больше, чем случаев, когда ни при одном бросании не появляются две шестерки одновременно? [99, с. 164–166].
1.1.8. Математика XVIII века. Эксперименты с бесконечностью
Математики XVIII века – это, прежде всего математики-прикладники. Все они много работали над решением прикладных задач, и их теоретические работы возникали на основе обобщения этих решений. Тесная связь с практикой влияла на стиль и характер изложения математических работ того времени. Первостепенное внимание уделялось не строгости изложения, а получению новых результатов.
Л. Эйлер довольно свободно обращался с бесконечными величинами и рядами, его методы были далеки от современных требований к строгости, и, тем не менее, окончательные выводы Л. Эйлера были, безусловно, верны.
Иногда говорят, что «от ошибок Эйлера оберегала интуиция». Сами по себе эти слова верны. Надо лишь уточнить, что речь идет не об интуиции как о каком-то врожденном качестве, присущем Эйлеру от природы. Интуиция Эйлера – это результат огромного количества выполненных им реальных расчетов и всесторонних проверок, которым подвергались результаты этих расчетов. Рассмотрим для иллюстрации одну работу Л. Эйлера. Она представит путь, на котором Л. Эйлер и другие математики XVIII века достигали правильных результатов.
Еще Я. Бернулли поставил задачу о вычислении суммы ряда обратных квадратов:
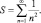 (1)
(1)
Однако задача оказалась трудной, и самим Я. Бернулли не была решена. Для ее решения Л. Эйлер использовал новый метод, основанный на смелом предельном переходе от конечных полиномов к бесконечным степенным рядам.
Современникам Эйлера было хорошо известно, что если полином степени 2n имеет вид
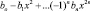
и имеет 2n различных корней:
?1; –?1; ?2; –?2; ...; ?n; –?n,
то его можно представить в виде:
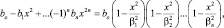
при этом коэффициент:
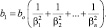 (2)
(2)
Л. Эйлер рассматривает функцию 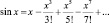 как «полином бесконечной степени», имеющий бесконечное число корней: 0; ?; –?; 2?; –2?… и т.д.
как «полином бесконечной степени», имеющий бесконечное число корней: 0; ?; –?; 2?; –2?… и т.д.
Далее Эйлер переходит к полиному 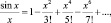 имеющему корни: ±?; ±2?; ...; ±n?, и по аналогии с конечными полиномами заключает, что
имеющему корни: ±?; ±2?; ...; ±n?, и по аналогии с конечными полиномами заключает, что
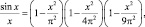 (3)
(3)
тогда с учетом равенства (2) имеем:
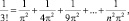
откуда и следует
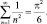 (4)
(4)
Л. Эйлер сам понимал, что его заключение о сумме ряда (1) «дерзко». Перенос свойств конечных полиномов на бесконечные степенные ряды мог привести и к ошибке, поэтому Эйлер счел необходимым многократно проверить свой метод и свой результат. Вот каковы были проверки, проделанные Эйлером.
1. Л. Эйлер вычислил сумму (1) приближенно, с точностью до шестого знака и нашел полное совпадение во всех знаках.
2. Пользуясь тем же методом исследования, но, сравнивая коэффициенты при х2 в равенстве (3), Л. Эйлер нашел сумму ряда 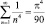 ,
,
и снова, вычисляя приближенно эту сумму прямым подсчетом, нашел полное совпадение до шестого знака.
3. Применяя тот же метод перехода от конечного полинома к бесконечному ряду для функции 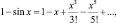 имеющей двойные корни, Л. Эйлер нашел сумму ряда
имеющей двойные корни, Л. Эйлер нашел сумму ряда 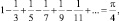 что совпало с уже известным результатом Г. Лейбница. «Для нашего метода, – писал об этом совпадении Л. Эйлер, – который некоторым может показаться недостаточно надежным, здесь обнаруживается великое подтверждение. Поэтому мы вообще не должны сомневаться в других результатах, выведенных тем же методом».
что совпало с уже известным результатом Г. Лейбница. «Для нашего метода, – писал об этом совпадении Л. Эйлер, – который некоторым может показаться недостаточно надежным, здесь обнаруживается великое подтверждение. Поэтому мы вообще не должны сомневаться в других результатах, выведенных тем же методом».
И все же Л. Эйлер не жалел сил для дальнейших проверок своего метода.
4. Л. Эйлер другим путем вычислил сумму ряда (1) и снова нашел, что 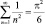 . Совпадение результатов, полученных двумя разными методами, было дополнительным доводом в пользу их правильности.
. Совпадение результатов, полученных двумя разными методами, было дополнительным доводом в пользу их правильности.
5. Даниил Бернулли (1700–1782) обсуждая результат Л. Эйлера, обратил внимание, что Л. Эйлером не доказано отсутствие комплексных корней в уравнении sinx = 0, наличие которых поставило бы под сомнение равенство (4). В ответ на эти сомнения Эйлер дополнительно доказал, что уравнение sinx = 0 не может иметь комплексных корней.
Легко убедиться, что все проверки, проделанные Л. Эйлером, не абсолютны, например, ясно, что из совпадения первых шести десятичных знаков суммы ряда (1) и числа 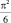 еще не следует с абсолютной достоверностью, что совпадут и все остальные знаки. Такие же замечания можно высказать и по поводу остальных пяти проверок. Но в целом проверки, проделанные Л. Эйлером, обеспечивали (по выражению А.Н. Крылова) «ту разумную строгость, которая, избавляя от ошибок, сообщает непреложность выводам».
еще не следует с абсолютной достоверностью, что совпадут и все остальные знаки. Такие же замечания можно высказать и по поводу остальных пяти проверок. Но в целом проверки, проделанные Л. Эйлером, обеспечивали (по выражению А.Н. Крылова) «ту разумную строгость, которая, избавляя от ошибок, сообщает непреложность выводам».
Проверки, проделанные Л. Эйлером, для подкрепления достоверности вычисления суммы (1) с особенной ясностью проявляют характерную черту математики XVIII века – преобладание прикладной математики и ее методов. Тщательные и многосторонние проверки – характерная черта прикладной математики (прикладной математикой мы называем решение задач физики, техники и т.п. математическими средствами). Естественно, что в прикладной математике проверка окончательного результата необходима и именно она гарантирует, что задача решена правильно. Пример с суммой ряда (1) показывает, насколько глубоко проникнут Л. Эйлер духом прикладной математики. Он применяет ее методы прямых проверок даже к задаче чистой математики – суммированию ряда несмотря на то, что любая прямая проверка относительна; она лишь повышает степень достоверности результата, не гарантируя его абсолютной истинности. Эйлер это понимал и именно поэтому не ограничивался одной единственной проверкой, он проверял свои результаты всесторонне, самыми различными методами.
Это приводит к пониманию причин того, что практически все результаты Эйлера (за самыми ничтожными исключениями) оказались справедливыми [70, с. 71–75].
1.1.9. Статистический эксперимент и вычисление числа ?
Французский естествоиспытатель Ж. Бюффон (1707–1788) в 1777 году опубликовал оригинальный способ вычисления числа ?, известный в литературе под названием «задача Бюффона». Существо этого способа кратко можно изложить так. Лист бумаги (плоскость) разграфлен параллельными прямыми, отстоящими друг от друга на расстоянии 2a. На него бросается («наудачу») игла длины 2l (l < a). Требуется найти вероятность пересечения иглы с какой-либо из этих прямых.
При решении этой задачи обозначают через x расстояние от центра иглы до ближайшей параллели, а угол, составленный иглой с этой параллелью, через ?. Требуется найти вероятность пересечения иглы с какой-либо из этих прямых. Все возможные положения иглы определяются точками прямоугольника со сторонами a и ?. Из рис. 2 видно, что для пересечения иглы с параллелью необходимо и достаточно, чтобы
x l sin .


Рис. 2. Задача Бюффона
Из сделанных предположений следует, что искомая вероятность равна отношению площади заштрихованной области к площади прямоугольника со сторонами a и ?. Следовательно, вероятность
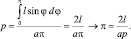
Поскольку вероятность p приближенно (в зависимости от числа бросаний иглы) равна отношению числа пересечений к числу бросаний иглы, то получается приближенная формула для вычисления числа ?:
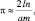
где n – число бросаний иглы; m – число наблюдаемых при этом пересечений. Этот способ в дальнейшем проверялся многими лицами. Так, например, Лаццарини в 1901 году бросал игру 3408 раз и получил значение ? = 3,1415929 [18, с. 95–96].
Многие способы приближенного вычисления числа ? были получены в результате большого числа проб. Например, итальянский геометр Маскерони (1750–1800) в 1779 году дал простой и практически ценный прием приближенного спрямления окружности с помощью одного циркуля. Как это делается? Описываем окружность с радиусом r = 1 (см. рис. 3). Этим же раствором циркуля, начиная от некоторой точки окружности А делаем засечки B, C, D. Тогда точки А, В, С, D будут вершинами правильного шестиугольника. Из точек А и D, как из центров, радиусом АС = DB проводим дуги СЕ и ВЕ. Затем из точки В, как из центра, радиусом ВЕ проводим дугу ЕМ, где М – точка пересечения этой дуги с основной окружностью. Тогда
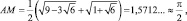
(«точное» же значение 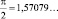 ) [18, с. 96].
) [18, с. 96].
1.1.10. Численный эксперимент как основа получения теорем геометрии
Теорема Л. Эйлера о многогранниках. Каждый многогранник имеет определенное число граней (Г), вершин (В) и ребер (Р). Соотношение между ними подметил впервые Л. Эйлер в 1750 г., оно выражалось формулой:
Г + В – Р = 2. (5)
Зная методы работы Эйлера (напомним, что из всех математиков Л. Эйлер писал о своих методах наиболее откровенно), нетрудно восстановить тот путь, которым Л. Эйлер пришел к формуле (5). Он начал с подсчета числа вершин, граней и ребер у конкретных многогранников. Экспериментируя с конкретными многогранниками, Л. Эйлер мог составить, например, следующую таблицу:
Многогранники | Г | В | Р |
Трехгранная пирамида | 4 | 4 | 6 |
Четырехгранная пирамида | 5 | 5 | 8 |
Трехгранная призма | 5 | 6 | 9 |
Куб | 6 | 8 | 12 |
Октаэдр | 3 | 6 | 12 |
Икосаэдр | 20 | 12 | 30 |
Додекаэдр | 12 | 20 | 30 |
Внимательно рассматривая подобные таблицы, он и подметил соотношение (5). От частного эксперимента к обобщению – это обычный путь естествоиспытателя. Однако для математики этого мало: формула (5) должна быть установлена не только для приведенных в таблице семи видов многогранников, но и для всех видов, а это означает, что формулу (5) требуется доказать. И Л. Эйлер представил такое доказательство, усовершенствовал которое О. Коши в 1811 году [70, с. 142–143].
Л. Эйлер обладал удивительной способностью открывать новые соотношения для натуральных чисел, изучая свойства некоторых первых чисел. Лишь потом ему (далеко не всегда!) удавалось найти строгие доказательства угаданных свойств. Так, с помощью индукции Л. Эйлер открыл замечательное тождество, связанное с суммой делителей натурального числа. Эйлер заметил, что для любого n выполняется равенство
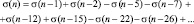
Здесь числа 1, 2. 5. 7, 12, 15, 22, 26, … попеременно выражаются формулами 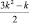 и
и 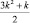 , где k = 1, 2, …, а знаки чередуются так, что после двух положительных слагаемых идут два отрицательных. Суммирование ведется до тех пор, пока аргументы функции ? неотрицательны; если последнее значение аргумента окажется нулем, то считается, что ?(0) = n.
, где k = 1, 2, …, а знаки чередуются так, что после двух положительных слагаемых идут два отрицательных. Суммирование ведется до тех пор, пока аргументы функции ? неотрицательны; если последнее значение аргумента окажется нулем, то считается, что ?(0) = n.
Эйлеру не удалось сразу найти доказательство формулы, он нашел его через год. Сам Эйлер по поводу наблюдений, приведших его к замечательным открытиям, написал следующее: «…в теории чисел, которая все еще не совершенна, наши самые большие надежды мы можем возлагать на наблюдения, они непрерывно будут вести нас к новым свойствам, которые позже мы будем стараться доказать. Этот вид знания, которое подкрепляется только наблюдениями и все еще не доказано, следует тщательно отличать от истины; оно, как обычно говорим, приобретается индукцией. … мы должны пользоваться таким открытием как возможностью более точно исследовать эти открытые свойства и доказать их или опровергнуть; в обоих случаях мы можем научиться кое-чему полезному» [27, с. 21–22].
1.1.11. Математика XIX–XX веков. Рождение компьютерного эксперимента
Проблема четырёх красок – математическая задача, предложенная Ф. Гутри в 1852 году. Теорема утверждает, что на сфере достаточно четырех красок для правильной раскраски любой возможной географической карты (т.е. такой раскраски, при которой любые две страны с общей границей не закрашены в один цвет). Первое доказательство было опубликовано А. Кемпе в 1879 году. Оно было признано достаточным выдающимися математиками того времени, и теорема считалась строго доказанной более десяти лет, пока в 1890 году П. Хивудом не была обнаружена ошибочность доказательства А. Кемпе. С тех пор, несмотря на многочисленные и упорные попытки многих математиков, доказательства теоремы не удавалось построить вплоть до семидесятых годов двадцатого века, когда к поиску были подключены быстродействующие цифровые вычислительные машины. Найденное с их помощью доказательство было опубликовано в 1976 году.
На этот раз «мысленный эксперимент» – математическое доказательство – оказался столь сложен, что оказалась полезной и необходимой помощь вычислительных машин.
Теорема о «четырех красках» оказалась первой, но, безусловно, не последней важной теоремой, доказанной уже не только человеком, но и машиной, а точнее – человеком, прибегнувшим к помощи вычислительной техники при доказательстве [70, с. 149–150].
Приведенные примеры из истории развития математической науки показывают, что к математическому решению и прикладных проблем, и теоретических ученые часто приходили используя эксперимент с объектами исследования (числовыми последовательностями, рядами, аналитическими выражениями, геометрическими фигурами, их реальными прототипами, моделями и т.п.). В математике, в отличие от естественных наук, эксперимент принимал и принимает самые различные формы: натурные эксперименты для получения эмпирических соотношений, модельные имитационные эксперименты для получения выводов по аналогии, численные эксперименты для получения обобщенных выводов и др.
Это ставит вопрос о связи естественнонаучных экспериментов и экспериментов, проводимых в математике. Требует раскрытия содержания понятие «математический эксперимент». В этой связи нашу точку зрения мы представим в следующем параграфе, исследуя специфику компьютерных экспериментов и методологии экспериментальной математики.