Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

2.1. Дидактическая модель исследовательского обучения в стиле экспериментальной математики

При построении модели мы будем опираться на следующие исходные данные, которые вытекают из информации, представленной в первой главе:

1. Исследовательское обучение математике в массовой школе – это включение на всех или некоторых этапах дидактического цикла в деятельность, сходную с деятельностью ученых в области экспериментальной математики.

2. Своеобразие методологии экспериментальной математики состоит в целесообразном использовании возможностей, предоставляемой экспериментальным и теоретическим подходами с привлечением средств компьютерной техники.

3. При проектировании каждого дидактического цикла учитель всякий раз принимает решение, какой подход: репродуктивный или исследовательский, и с какой степенью полноты применять на каждом из этапов с учетом, по крайней мере, трех основных факторов: М-уровня базовой математической подготовки учащихся (для обозначения фактора выбрана первая буква слова «mathematics», I-уровня сформированности у учащихся качеств математика-экспериментатора и математика-теоретика (для обозначения фактора избрана первая буква слова «inquiry») и Т-лимита учебного времени, отведенного на изучение материала (для обозначения уровня избрана первая буква слова «time»).

Метод компьютерного эксперимента применим для достижения целей любого этапа дидактического цикла.

Целью построения дидактической модели является исследование влияния сочетания текущих значений факторов: M(t); I(t); T(t), на принятие учителем решения о степени отражения стиля экспериментальной математики на отдельных этапах дидактического цикла обучения математике.

Теперь разберемся с тем, какой смысл мы будем вкладывать в термин «модель». Наиболее часто, в основу кладут определение, данное В.А. Штоффом: «Под моделью понимается такая мысленно представляемая или материально реализованная система, которая, отражая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает нам новую информацию об объекте» [100, с. 19].

Данное определение включает в себя четыре свойства этого понятия:

– мысленная или материальная система;

– заместитель объекта исследования;

– носитель значимых свойств объекта исследования, отраженных в исходной информации о нем;

– средство для получения новой информации об объекте исследования.

В данном параграфе мы вынуждены будем несколько отойти от такого понимания модели в силу следующих причин:

1. Дидактическая модель, которую мы собираемся представить, является заместителем не одного, а двух объектов: дидактического цикла обучения математике (А) и гносеологического цикла экспериментальной математики (В).

2. Описываемая нами дидактическая может быть призвана отражать не только основные свойства этих объектов, но и тесноту связи (С) между их свойствами.

3. Значение тесноты связи между свойствами этих объектов не может быть зафиксировано в модели однозначно, так как зависит от текущих (изменяющихся во времени t) значений набора, по крайней мере, трех факторов: М (t) – уровня базовой математической подготовки учащихся достигнутого к моменту времени t, I (t) – уровня сформированности у них качеств математика-экспериментатора и математика-теоретика достигнутого к моменту времени t и Т (t) – имеющегося в данный момент лимита учебного времени на изучение материала.

4. Назначение этой модели также отличается от указанного В.А. Штоффом, так как дидактическая модель носит предпроектный характер, то есть призвана служить информационной основой для проектирования такого процесса исследовательского обучения математике в стиле экспериментальной математики, который обеспечивает становление у учащихся элементов стиля мышления математика-экспериментатора, находящихся в зоне ближайшего развития в момент времени t.

В рамках данного исследования, в связи с этими причинами, под дидактической моделью исследовательского обучения в стиле экспериментальной математики мы будем понимать информационную систему, характеризующую полноту реализации на этапах дидактического цикла обучения математике гносеологического цикла экспериментальной математики.

В основу представления данной модели мы положили граф соответствия, предложенный А.В. Ястребовым:

«Определение. Графом соответствия между двумя рядами объектов A1, A2, ..., Ak и B1, B2, ..., Bn называется прямоугольная таблица, обладающая следующими свойствами:

1) строки таблицы занумерованы с помощью объектов A1, A2, ..., Ak;

2) столбцы таблицы занумерованы с помощью объектов B1, B2, ..., Bn;

3) в клетке, соответствующей строке Ai и столбцу Bj, содержится информация Сij о взаимосвязи этих объектов» [104, с. 92].

В качестве объектов графа будут выступать две группы однородных элементов, между которыми должна быть раскрыта связь:

– Этапы дидактического цикла процесса обучения[15], описанные Л.Я. Зориной в [41], которые мы адаптировали к особенностям процесса обучения математике: A1 – постановка дидактической цели и принятие ее учащимися; А2 – актуализация базовых знаний; А3 – изучение нового; А4 – освоение нового материала в ходе решения задач на его применение; А5 – рефлексия результатов обучения и определение направлений дальнейшей работы.

– Этапы элементарного цикла научного познания в экспериментальной математике: В1 – постановка математической задачи; В2 – обоснование необходимости привлечения компьютерного эксперимента; В3 – планирование эксперимента; В4 – создание или выбор средств проведения компьютерного эксперимента; В5 – сбор и анализ данных эксперимента; В6 – использование результатов компьютерного эксперимента для решения задачи; В7 – развитие идеи решенной задачи.

Для решения главного вопроса о том, целесообразна ли организация исследовательского обучения в стиле экспериментальной математики на данном этапе дидактического цикла и насколько полно должны быть представлены в нем все этапы гносеологического цикла экспериментальной математики, нам придется воспользоваться числовым представлением значения тесноты связи (Сij) между Аi и Bj. Теснота связи представляет собой расчетную переменную, так как ее значение зависит от значений факторов Мij(t); Iij(t); Tij(t).

	А1	А2	А3	А4	А5
В1	С11	С12	С13	С14	С15
В2	С21	С22	С23	С24	С25
В3	С31	С32	С33	С34	С35
В4	С41	С42	С43	С44	С45
В5	С51	С52	С53	С54	С55
В6	С61	С62	С63	С64	С65
В7	С71	С72	С73	С74	С75

Силой тесноты связи Сij определяется целесообразность включения учащихся на этапах дидактического цикла в деятельность проведения эксперимента и их степень самостоятельности в реализации его этапов.

Смысл рассматриваемых нами величин Сij, несколько варьируется и определяется занимаемой в матрице позицией:

С1j, 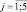– характеризуют наличие действий учащихся по постановке исследовательской математической задачи и степень отражения в этих действиях методологии экспериментальной математики.

С2j, 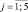– характеризуют наличие в деятельности учащихся по решению поставленной задачи действий, направленных на обоснование необходимости привлечения компьютерного эксперимента и степень отражения в этих действиях методологии экспериментальной математики.

С3j, 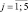– характеризуют вовлеченность учащихся в деятельность планирования компьютерного эксперимента.

С4j, 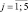– характеризуют вовлеченность учащихся в деятельность выбора или создания средств проведения компьютерного эксперимента.

С5j, 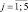– характеризуют степень полноты реализации учащимися действий по проведению эксперимента и анализа его ре-
зультатов.

С6j, 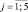– характеризуют степень отражения методологии экспериментальной математики в деятельности учащихся по использованию результатов экспериментального исследования для дальнейшего решения задачи.

С7j, 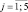– характеризуют наличие и степень отражения методологии экспериментальной математики в деятельности учащихся по постановке новых задач на базе решенной.

Значения Сij, при фиксированном значении j в некоторой степени зависят от значения С1j. Например, если С1j = 0, то и осталь-
ные Сij = 0.

Смысл Сij, при фиксированном значении j определяется видом эксперимента, который проводится на j-м этапе дидактичес-
кого цикла.

Перечень образовательно значимых видов экспериментов представлен нами в табл. 1 с указанием их возможных функций, отнесенных к этапам дидактического цикла.

Приведем примеры перечисленных видов экспериментов в табл. 1.

Таблица 1

Виды экспериментов, применяемых
в ходе исследовательского обучения математике

Аi	Вид	Функции
А1, А5	Конструктивный эксперимент	конструктивная проверка существования объекта исследования (изучения), оценка адекватности модели объекта исследования (изучения) исходным данным, конструирование инструментов (средств, оборудования) или объяснение механизмов их работы, разработка инструкций, рекомендаций по их использованию
А2, А4	Иллюстративный эксперимент	визуализация утверждений как поддержка работы памяти или достижение понимания
А3	Разведочный эксперимент	использование модели для сбора экспериментальных данных, позволяющих выдвинуть гипотезы о свойствах и связях изучаемых объектов
А2, А4	Контрольный эксперимент	контроль преобразований и вычислений, фальсификация, верификация гипотез
А1, А5	Модифицирующий эксперимент	обнаружение ограниченности знаний, определение направления развития идеи, постановка новых задач

Пример 1 (модифицирующий эксперимент этапа А1).

Тема урока «Взаимное расположение прямых в пространстве». Решите серию заданий на динамическом листе GeoGebra (рис. 14 и 15) и сформулируйте вопросы, поиску ответов на которые будет посвящен этот урок.

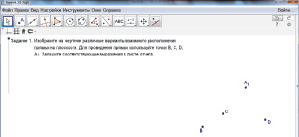
Рис. 14. Задание для актуализации планиметрических понятий

В ходе решения первой задачи учащиеся актуализируют знания о существовании двух видов отношений взаимного расположения прямых на плоскости (пересечение, параллельность). Иллюстрируют актуализированные понятия построением прямых, проходящих через представленные на экране точке с использованием инструментов GeoGebra: «Прямая», «Параллельная прямая».

При выполнении второго задания, ученики обнаруживают, что выразительных возможностей их математического языка недостаточно для записи результатов наблюдения за изменением отношения взаимного расположения построенных прямых при «выходе в пространство». Это приводит к постановке познавательных вопросов: «Какие прямые можно называть параллельными в пространстве?», «Существуют ли в пространстве прямые, которые нельзя назвать ни пересекающимися, ни параллельными?»

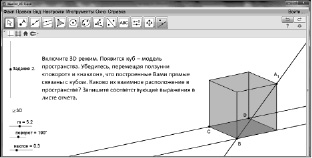
Рис. 15. Задание для «выхода в пространство»

Пример 2 (иллюстративный эксперимент этапа А2).

В учебнике геометрии для 9 класса дано следующее определение правильного многоугольника: «Правильным называется выпуклый многоугольник, у которого все стороны равны и все углы равны». Покажите, что все свойства, указанные в этом определении важны. Для этого постройте: 1) невыпуклый многоугольник, у которого все стороны и все углы равны; 2) равноугольный, но не равносторонний выпуклый многоугольник; 3) равносторонний, но не равноугольный выпуклый многоугольник.

Учащиеся могут выполнять построение как на клетчатой бумаге, пользуясь только линейкой и карандашом, или на нелинованной бумаге с использованием циркуля и линейки, так и на компьютере (рис. 16). В результате формируется набор фигур, которые не удовлетворяют определению правильного многоугольника, но обладают некоторыми свойствами данного понятия. Это примеры звездчатых и полуправильных многоугольников.

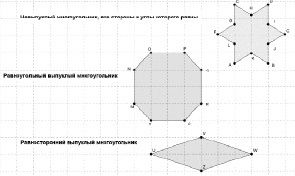
Рис. 16. Пример результата иллюстративного эксперимента

Пример 3 (разведочный эксперимент этапа А3).

Проведите эксперимент, позволяющий выяснить, существует ли неравносторонний треугольник, в котором наименьшая медиана равна наибольшей высоте [19]. Найдите способ доказательства справедливости Вашей гипотезы.

Создадим модель треугольника АВС с наибольшей стороной АС и наименьшей – АВ. Проведем к его наибольшей стороне медиану ВЕ, а к наименьшей – высоту СН. Меняя положение вершины С при фиксированном положении точек А и В можно добиться такого положения точки С чтобы медиана ВE имела длину равную высоте СH с заданной точностью (рис. 17).

Малые шевеления точки С показывают, что при малых изменениях длины СН длина отрезка ВE также меняется не значительно. Это наводит на мысль о непрерывности, связывающей их функции.

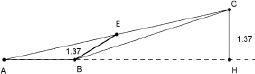
Рис. 17. Результат разведочного эксперимента

Допустим, что длины отрезков CH и BE связаны непрерывной функцией. Пусть вершина С движется по окружности радиуса ВС (рис. 18). Тогда, если угол АВС прямой, то СН и ВС совпадают. Так как ВС – больший катет, то BE < СH. Если угол АВС близок к развернутому, то BE приближается по длине к BS, S – середина AD, СH – приближается к нулю. Следовательно, BE > СH. В силу непрерывности функции существует такое промежуточное значение, при котором BE = СH.

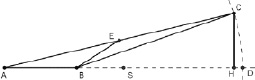
Рис. 18. Чертеж для поддержки доказательных рассуждений

Пример 4 (контрольный эксперимент этапа А4).

Обобщим теорему Пифагора. Получим следующее утверждение: «Если на сторонах прямоугольного треугольника построены правильные многоугольники с одинаковым числом сторон, то площадь многоугольника построенного на гипотенузе равна сумме площадей многоугольников, построенных на его катетах». Проверьте допустимость такого обобщения компьютерным экспериментом.

Для проверки утверждения, учащиеся должны сначала подготовить динамический чертеж, позволяющий просмотреть ситуацию для целого спектра прямоугольных треугольников. Для этого можно задать прямоугольник по произвольно выбранному катету и угловому параметру ? ? [0; 90°], h = 1°. На сторонах треугольника во внешнюю сторону с помощью инструмента «правильный многоугольник» отложить многоугольники, число сторон которых зависят еще от одного параметра n, принимающего целочисленные значения, например из промежутка
[3; 300]. С помощью инструмента «Площадь» вычислить их площади. Затем, пользуясь строкой ввода, создать переменную, равную сумме площадей многоугольников, построенных на катетах (рис. 19). Эксперимент состоит в изменении значений параметров n и ? (последовательном или хаотичном) с оценкой сохранения равенства при разных наборах значений параметров.

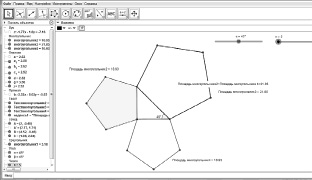
Рис. 19. Рабочий динамический чертеж для проведения контрольного эксперимента

Пример 5 (конструктивный эксперимент этапа А5).

Создайте инструмент для построения ГМТ, равноудаленных от заданной окружности и некоторой точки плоскости.

Построение данного инструмента требует от учащихся сначала переосмысления имеющегося знания о понятии «расстояние», формулировании на этой основе понятия «расстояние от точки до окружности», а затем создания способа построения элемента ГМТ (рис. 20).

Полученный динамический чертеж и становится основой для создания требуемого виртуального инструмента (рис. 20).

Текущие значения тройки основных факторов (M(t); I(t); T(t)) позволяют определить целесообразность включения в процесс обучения экспериментов разных видов, перечисленных выше, а также выявить и осмыслить степень самостоятельности, с которой учащиеся могут и должны участвовать в этих экспериментах на отдельных этапах. Рассмотрим подробнее значения, которые может принимать каждая из этих переменных.

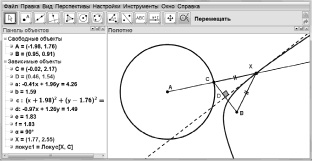
Рис. 20. Чертеж для создания нового инструмента

Возможность всякого исследования, как известно, определяется уровнем математической подготовки исследователя и уровнем овладения математическими основами исследования. В этой связи мы будем говорить не об общекультурном уровне математической подготовки учащегося, а об уровне его математической подготовки, достаточном для освоения запланированного учителем элемента предметного содержания в исследовательской деятельности.

Объем имеющихся у учащихся знаний должен быть таким, чтобы обеспечить им возможность создания чувственного образа объекта исследования на основе исходных данных, конструирования его исследовательской модели, преобразования исходных данных и чувственного образа. Этими соображениями определяется принятие следующей квалиметрической шкалы оценки уровня математической подготовки учащегося (М) (см. шкалу 1).

Значения 0 и 3 в этой шкале являются предельными, так как М = 0 закрывает возможность организации продуктивной деятельности не только теоретического характера, но и экспериментального; М = 3 предоставляет возможность свободного выбора или даже сочетания стилей продуктивной деятельности в учебном познании.

Шкала 1

Значения		Характеристика достаточности теоретического базиса для осуществления исследовательских действий
Mt
0	0	Учащийся не обладает математическими знаниями, которые необходимы для осознанного восприятия исследования в стиле экспериментальной математики
1	0,17	Учащийся имеет знания для осознанного восприятия образца исследования, но этих знаний недостаточно для самостоятельной реализации данного этапа исследования
2	0,33	Учащийся не имеет знаний для самостоятельной реализации теоретической части исследования, но обладает знаниями для реализации его экспериментальной части
3	0,5	Учащийся обладает знаниями как для реализации экспериментальной, так и теоретической частей исследования
6	1	Сумма

Вторым важнейшим фактором, обеспечивающим возможность освоения содержания в исследовательской деятельности, является владение методологическими основами исследования. Степень самостоятельности учащихся в проведении учебных исследований, отнесенных к стилю экспериментальной математики, определяется уровнем развития у них соответствующих методологических знаний об экспериментальных методах в математике. В монографии [96] нами было показано, что развитие методологических знаний сопровождается изменением формы их существования (неявные личностные знания – неявные; затем частично-выявленные межличностные знания – объективизированные надличностные знания), сопровождаемым двумя процессами: их рационализацией и генерализацией. Методологические знания зарождаются в момент инсайта (озарения) или передаются в процессе восприятия образцов деятельности, предъявляемых учителем. Осознание экстрапознавательной значимости методологического знания происходит постепенно в ходе накопления представления о других ситуациях успешного применения возникшей идеи. Объективизация методологического знания начинается со столкновения с ситуациями его неэффективности при попытках вскрытия причин этой неэффективности. Объективизация является необходимой основой для возникновения способности к осознанной саморегуляции использования методологических знаний, включая способность критической оценки типичного стиля, варьирования и сочетания стилей. Эти соображения положены нами в основу построения квалиметрической школы уровня сформированности опыта исследовательской деятельности (I) в стиле экспериментальной математики (см. шкалу 2).

Шкала 2

Значения		Показатели уровня методологических основ деятельности в стиле экспериментальной математики
It
0	0	Учащийся не имеет образца деятельности в стиле экспериментальной математики в сходной ситуации
1	0,07	Учащийся обладает представлениями (неявными методологическими знаниями), которые тесно связаны с конкретным образцом познавательной деятельности
2	0,13	Учащийся обладает частично-выявленными методологическими знаниями, которые являются отражением речевых комментариев учителя при демонстрации образцов, но не имеет собственного опыта их использования
3	0,2	Учащийся обладает частично-выявленными методологическими знаниями, которые являются отражением текста инструкций, наводящих вопросов, указаний учителя, а также имеет опыт реализации плана экспериментального исследования по инструкции
4	0,27	Учащийся обладает частично-выявленными методологическими знаниями, которые являются отражением результата эвристических бесед и методологической саморефлексии в сократовском диалоге, а также опытом использования этих знаний для планирования познавательной деятельности в стиле экспериментальной математики
5	0,33	Учащийся обладает объективизированными методологическими знаниями, а также опытом их использования для определения методологической базы исследования, включающей методы, отнесенные как к экспериментальному, так и теоретическому подходам
15	1	Сумма

Значения 0 и 5 являются предельными в данной шкале: I = 0 делает невозможным включения учащихся в продуктивную деятельность в стиле экспериментальной математики даже при активной помощи учителя; I = 5 обеспечивает учащимся возможность самостоятельного выбора и сочетания подходов к исследованию для решения поставленной проблемы.

Исследовательская деятельность даже при достаточном уровне подготовки учащегося требует значительных затрат времени. В связи с этим выбор способа учебного познания и степень самостоятельности учащихся определяются лимитом учебного времени, который целесообразно описать с использованием шкалы 3.

Шкала 3

Значения		Лимит времени на достижение цели дидактического этапа
Tt
0	0	Нет времени на организацию продуктивной деятельности учащихся
1	0,17	Организация продуктивной деятельности возможна, но на ее реализацию отведена лишь часть урока
2	0,33	На реализацию продуктивной деятельности отведен целый урок или учебная пара
3	0,5	Продуктивная деятельность осуществляется во внеурочное время, т.е. не ограниченна лимитом времени
6	1	Сумма

Значения 0 и 3 также являются предельными в данной шкале. T = 0 требует организации на уроке лишь репродуктивной деятельности или предъявления учащимся готовых образцов исследовательской деятельности в стиле экспериментальной математики; Т = 3 позволяет реализовать гносеологический цикл в полном объеме с наибольшей степенью самостоятельности учащегося.

Таким образом, принятие решения о степени отражения методологии экспериментальной математики в процессе обучения (Cij) является многокритериальной задачей оптимального выбора, т.е. (Cij) = f (M; I; T). Формальное решение этой задачи требует использования такого обобщенного критерия, при котором (Cij) = f (M; I; T), где f (M; I; T) ? [0; 1], поскольку значения функции f (M; I; T) интерпретируются нами как теснота связи элементов дидактического цикла с элементам гносеологического цикла в стиле экспериментальной математики.

Кроме того мы задали начальные значения шкал таким образом, что (Cij) = f (0; I; T) = f (M; 0; T) = f (M; I; 0) = 0. Это определяет необходимость использования мультипликативного критерия: (Cij) = k · M · I · T. Значение коэффициента k определено тем, что f (0,5; 0,33; 0,5) = 1. В результате получаем формулу:

(Cij) = k·M·I·T. (*)

Классификация уровней исследовательского обучения по степени полноты отражения в нем черт исследовательской деятельности ученых Х. Банчи и Р. Белла [109] позволяет нам интерпретировать значения мультипликативного критерия для средних значений Сij 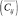c фиксированным значением j следующим образом:

Уровень 1 (Reproductive education or Confirmation Inquiry). Репродуктивное обучение или Экспериментальное подтверждение элемента содержания, вводимого в готовом виде на данном этапе дидактического цикла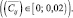

Поскольку в условиях, соответствующих значениям ,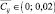
элемент дидактического цикла i не может быть реализован в соответствии с элементом j гносеологического цикла экспериментальной математики при активном участии учащихся, учитель предъявляет учащимся информацию в готовом виде, дополняя ее демонстрацией образца применения экспериментального подхода для ее получения или понимания.

Уровень 2 (Structured Inquiry). Проведение исследований в стиле экспериментальной математики по заданному плану .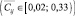

Условия, соответствующие значениям 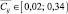, требуют инструктивной помощи учащимся при осуществлении ими исследовательских действий элемента j на этапе дидактического цикла i. Степень и характер этой помощи определяется конкретным набором значений
(M; I; T). Он варьируется от синхронных действий учителя и учащихся до действий, степень свободы которых определяется свойствами динамического рабочего листа или степенью подробности плана.

Уровень 3 (Guided Inquiry). Проведение исследований в стиле экспериментальной математики под руководством учителя .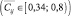

Условия, соответствующие значениям 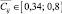определяют возможность реализации этапа i дидактического цикла в соответствии с характером исследовательской деятельности элемента j гносеологического цикла экспериментальной математики, но с помощью учителя. Однако, в отличие от предыдущего этапа, помощь реализуется посредством вовлечения учащихся в эвристическую беседу или сократовский диалог, оказанием им помощи за счет предъявления динамического листа ограниченного уровня интерактивности без указания способа его использования.

Уровень 4 (Open/True Inquiry). Свободные подлинные исследования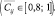

Условия, соответствующие значениям 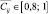достаточны для реализации i-го этапа дидактического цикла в полном соответствии с характером исследовательских действий, определенным j-м этапом экспериментального исследования. Они достаточны также и для принятия учащимся решения об отказе от использования экспериментального подхода или сочетания с теоретическим подходом.

В зависимости от набора конкретных значений Сij при фиксированном j исследовательское обучение на каждом уровне реализуется по-разному:

– учащимся предоставляется различная степень самостоятельности с учетом актуального уровня математической подготовки и подготовки к исследовательской деятельности;

– для оказания помощи учащимся при деятельности в зоне ближайшего развития используются разные средства помощи: образцы, инструкции, планы, динамические листы разного уровня интерактивности, эвристические и сократовские диалоги.

Для простоты использования модели все возможные значения Сij, определяемые наборами (М, I, T), нами рассчитаны и представлены в приложении 1.

Прежде чем переходить к демонстрации конкретных примеров использования представленной модели нам необходимо осветить вопросы, связанные с отбором тех экспериментов, методологией которых учащиеся общеобразовательной школы должны овладеть в период обучения в школе. Также важно раскрыть суть разработки и применения предлагаемых нами средств оказания помощи учащимся. Эти вопросы мы собираемся осветить в последующих параграфах.