Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

2.2. Содержательные основы воспитания математика-экспериментатора

В данном параграфе мы остановимся на содержательных основах исследовательского обучения в стиле экспериментальной математики.

Для того, чтобы становление мировоззрения математика-экспериментатора не проходило стихийно и бесконтрольно, в содержании школьного курса математики, по нашему мнению, должна быть выделена и специально спроектирована особая содержательно-методическая линия. Мы ее назвали линией экспериментальной математики.

Выделение данной линии, по нашему мнению, может быть осуществлено без каких-либо существенных расширений учебных программ по математике, а лишь за счет «вывода из подполья» математических экспериментов, так или иначе привлекаемых к процессу обучения. Для демонстрации этого обратимся к теоретическим основам проектирования содержательно-методических линий.

Данное понятие вошло в теорию и методику обучения математике в 50-е годы XX века в результате длительного поиска учеными (В.Л. Гончаров и др.) специфической категории, при помощи которой можно было бы вводить требования к реализации внутрипредметных связей при проектировании содержания обучения математике и описывать результаты логико-дидактического анализа развертывания содержания обучения в учебниках математики разных авторов [34].

А.Я. Блох определил это понятие как «сечение курса школьной математики, в которое попадают тематически и идейно связные, но композиционно разъединенные фрагменты учебников. Материал, относящийся к каждой линии, изучается длительное время, нередко на протяжении всего курса, так что ее можно рассматривать с точки зрения установления и внутрипредметных преемственных связей» [21, с. 35].

Первоначально данное понятие применялось только к раскрытию связей тех элементов содержания математического образования, которые представлены учебным материалом учебников, объединенным вокруг фундаментального понятия математики (ведущего понятия линии):

– определениями или, по крайней мере, описаниями, фундаментального понятия и видовых понятий;

– свойствами и признаками, по крайней мере, видовых понятий;

– утверждениями о связи данного понятия с другими понятиями математики.

Выделялись семь основных линий: числа и выражения, выражения и их преобразования, уравнения и неравенства, функций и элементы математического анализа, геометрические фигуры и измерение геометрических величин, позднее стохастическая линия.

Впоследствии стали говорить о целесообразности рассмотрения линий, которые представлены в учебниках лишь задачным материалом и описаниями образцов математической деятельности, что является проявлением деятельностно-продуктивного дуализма математики: алгоритмическая (ведущее понятие «алгоритм»), прикладная (ведущее понятие «математическая модель»), логическая (ведущее понятие «доказательство») и др.

Далеко не все фундаментальные понятия этих линий терминологически обозначены в учебниках, об их содержании и объеме учащиеся могут получить представление лишь в результате саморефлексии, а также рефлексивного анализа представленных в учебниках образцов деятельности.

А.Я. Блох назвал такие содержательно-методические линии невыявленными, обратив при этом внимание на относительность разделения линий на выявленные и невыявленные: «Следует сказать, что выявленность – относительная характеристика линии. Она зависит от многих причин, в частности, от той эпохи или исторического периода, к которой относится создание анализируемого курса, от учебника, в которых эти курсы реализованы» [21, с. 51]. В подтверждение этому он привел пример функциональной линии, которая до 50-х годов XX века была представлена в учебниках лишь образцами применения линии функциональной зависимости.

Е.И. Лященко описала содержательно-методологические линии, подчеркнув тем самым их деятельностный характер, отнеся к ним линию математического языка, доказательств, сюжетных задач: «Материал этих линий и его функции находятся «над» конкретным математическим содержанием, организованным в содержательно-методические линии, и помогает раскрыть специфику и общность материала разных предметных линий. Реализация методологических линий помогает лучше познать и понять предметные линии» [56, с. 129].

Обращая внимание на связь содержательно-методических линий школьного курса математики с математическими структурами, В.А. Тестов назвал линии этого типа «схемами мышления». Значимость их выделения и целенаправленного формирования обосновывается им следующим образом: «… для обеспечения математического развития школьников и студентов должны быть сформированы не только алгебраические, порядковые и топологические структуры, которые представляют собой, прежде всего, системы хранения знаний. Необходимо сформировать и структуры, которые выше мы назвали математическими когнитивными схемами (термин М.А. Холодной) и которые представляют собой определенные качества математического мышления, которые являются, прежде всего, средствами, методами познания. Поэтому такие структуры можно также назвать схемами математического мышления» [87, с. 82]. К математическим схемам мышления от отнес: логические, алгоритмические, комбинаторные и образно-геометрические структуры.

Таким образом, речь не идет о дополнении учебных программ по математике новым содержанием, а об оформлении в отдельную содержательно-методическую линию образцов деятельности, раскрывающих содержание и объем фундаментального (ведущего) понятия «математический эксперимент», с целью создания условий для формирования на этой основе у учащихся качеств математика-экспериментатора.

Сегодня, на наш взгляд, сложились исторические условия, благоприятные для решения этой задачи, подобные тем, которые в математической науке вывели «из подполья» экспериментальные методы и привели к оформлению методологии экспериментальной математики.

Подчеркивая эту аналогию, а также аналогию с экспериментальной и теоретической частью школьного курса физики и химии, мы посчитали возможным назвать ее линией экспериментальной математики.

Таким образом, под линией экспериментальной математики мы понимаем содержательно-методологическую линию школьного курса математики, ведущим понятием которой является понятие математического эксперимента.

А.Я. Блох сформулировал несколько проблем проектирования таких линий. По его мнению, главной проблемой является «выбор материала, на котором происходит формирование содержания этой линии. Этот материал может быть специфическим для ведущего понятия линии, характеризующим его теоретическое содержание, или неспецифическим, относящимся к основному содержанию курса» [21, с. 51].

Проблему проектирования неспецифического содержания данной линии мы решаем, опираясь на данные о той роли, которую сыграли экспериментальные методы в получении научных результатов, описанных в параграфе 1.1 и составляющих сегодня содержание школьного курса математики. Специфическое содержание линии определяется нами на основе данных о методологических основах экспериментальной математики, представленных в параграфе 1.2.

Второй, из обозначенных А.Я. Блохом проблем, является определение оптимального уровня и полноты выявленности специфического содержания ведущего понятия данной линии – понятия «математический эксперимент».

В решении этого вопроса мы будем опираться на разработанную нами концепцию проектирования методологической составляющей школьного курса математики [97].

Главным положением этой концепции является постепенность выявления элементов специфического содержания содержательно-методологической линии, подчиняющегося общим закономерностям процессов рационализации и генерализации методологических оснований деятельности.

Процесс рационализации – это процесс эволюции методологических знаний (МЗ), сопровождающийся изменением формы их существования и содержания.

Поскольку методологическое знание исторически возникло в связи с потребностью обобщения опыта (генерализации) познавательной деятельности для его передачи, установления условий эффективности, решения вопросов выявления фальсификаций и верификации гипотез, то процесс рационализации сопровождается и генерализацией методологических знаний.

Характеристика методологических знаний на различных этапах их эволюции и условия наступления этапа представлены в табл. 2.

Таблица 2

Основные этапы эволюции методологических знаний

Кроме того, процесс эволюции методологических знаний характеризуется следующими основными особенностями:

– основным условием, обеспечивающим динамику этого процесса, является развитие научных знаний;

– одновременно в процессе познания функционируют методологические знания, находящиеся на разных стадиях процесса своего развития;

– процесс эволюции различных методологических знаний наряду с общими чертами имеет и свои особенности;

– некоторые методологические знания могут быть опредмечены математической наукой (т.е. превращены в предметные знания математики).

В монографии «Методология учебного познания как цель изучения математики» М.В. Шабановой показано, что по характеру ведущей формы познания в школьном курсе математике можно выделить: метаэмпирическую форму познания (1–6 классы) и метаэмпирическую форму познания с элементами дедукции (7–11 классы). Первые создают благоприятную содержательную основу реализации первых двух этапов развития методологических знаний об экспериментах (зарождение и распространение), использовавшихся в период зарождения математики. Вторые актуальны для реализации третьего этапа (объективизация) сформированных неявных знаний, а также для развития представлений (с последующей объективизацией) о специфике математических экспериментов, включая мыслительные и компьютерные; о возможностях и ограничениях экспериментальных методов, их связи с теоретическими методами познания; возможностях и условиях рационального использования экспериментов на разных этапах гносеологического цикла.

Анализ рабочих программ по математике позволяет наметить неспецифическое содержание линии экспериментальной математики, обеспечивающее развитие перечисленных выше методологических знаний.

1. Развитие линии экспериментальной математики в начальной школе. Изучение математики в начальной школе предоставляет возможности и условия для продуктивного формирования базовых умений, связанных с реализацией экспериментального подхода при изучении математики, так как все правила математических действий формируются в этот период как индуктивные обобщения частных закономерностей, к обнаружению которых учащиеся пришли случайно или по заданию учителя.

Первые математические знания складываются у учащихся на основе предметных действий (пересчет и сравнение групп предметов). Это является благоприятной основой для зарождения и накопления представлений опыта использования натурных экспериментов бэконовского типа. К потребности их проведения обычно приводят вопросы, типа «Что, если попробовать сделать так?» «А что произойдет, если …?» и т.п., которые возникают в ходе решения задач других линий.

Овладение этим видом экспериментов проявляется в способности подмечать закономерности при выполнении одних и тех же заданий с объектами разной природы, абстрагируясь от их природы, а также в способности видеть причины сходства и различия результатов одних и тех же практических действий в, казалось бы, сходных условиях и использовать их для рационализации рутинных действий.

Зарождению представлений об экспериментах бэконовского типа способствует постановка заданий на выполнение серии практических действий, с последующей вербализацией способа их выполнения.

Пример 1. Задание на сравнение количеств объектов.

1. На столе лежат коробочки со счетными палочками. Определите, в какой коробочке палочек больше всего, в какой – меньше всего.

2. На столе расставлены куклы, машинки и кубики. Определите, каких игрушек на столе больше всего, каких – меньше всего.

3. На столе разбросаны разные письменные принадлежности и стоят три стаканчика. Соберите в стаканчики письменные принадлежности так, чтобы в каждом оказались принадлежности только одного вида. Определите, каких игрушек на столе было больше всего, каких – меньше всего.

Расскажите, что общего в этих заданиях. Расскажите, как вы сравнивали множества предметов в каждом задании.

Переход от осуществления действий с предметами к действиям с числами и геометрическими фигурами, который начинается с вопроса изучения нумерации чисел в пределах десятка, создает условия для распространения бэконовского типа экспериментирования на деятельность с вещественными моделями математических объектов и математическими символами. Для этих целей могут быть использованы задания, в ходе выполнения которых у учащихся возникают естественные потребности рационализации выполняемых математических действий.

Пример 2. Найдите сумму пересчетом:

а) 6 + 2;

б) 7 + 3;

в) 3 + 5;

г) 1 + 8;

д) 3 + 7;

е) 2 + 6.

Предложите способ, который позволит сэкономить время.

Данное задание выполняется учащимися на основе сформированных навыков вычисления суммы пересчетом предметов. Серия примеров составлена так, чтобы, вовлекая учащихся в деятельность применения метода пересчета в концентре «Десяток», вызвать у них неудовольствие от определения суммы данным методом. Это неудовольствие усиливается в серии примеров за счет включения в нее пар, содержащих одинаковые результаты, но значительно отличающихся по трудности пересчета (a–e; б–д). Это создает условия для обнаружения учащимися переместительного закона сложения, который позволяет сократить пересчет присоединяемой груп-
пы объектов.

Подобного типа задания могут быть использованы на более поздних этапах изучения математики.

Пример 3. На листе бумаги нарисовано три многоугольника (рис. 21). Найдите их площади. Придумайте способ, как сделать это быстро.

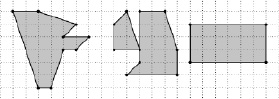
Рис. 21. Многоугольники

Эта задача может быть предложена ученикам 8 класса при изучении темы «площадь». Они легко найдут площадь прямоугольника по известной формуле. Так как виды остальных фигур им неизвестны, то им придется придумывать способы, связанные с достраиванием фигур до известной или разрезанием на части. В ходе реализации второй идеи они быстро догадаются, что все фигуры состоят из одного и того же набора частей, а значит, площади их равны. Этот вывод, как полезный и важный, будет зафиксирован с помощью учителя в виде теоремы о равенстве площадей равносоставленных планиметрических фигур.

Следующим видом экспериментов, с которыми знакомятся учащиеся при изучении математики в начальной школе, являются эксперименты аристотелевского типа. Их главным отличием от экспериментов бэконовского типа является активный характер по отношению к объекту изучения. На этом этапе происходит обучение планированию экспериментов, целенаправленному их проведению и получению адекватных выводов. Вводится специальные термины, учащиеся узнают о различном назначении экспериментов в математическом познании, кроме того учащиеся знакомятся с различными видами вещественных (интерпретационные) модели изучаемых математических объектов, осваивают способы их создания и целесообразного использования.

Зарождению первых представлений о возможности активного воздействия на объект изучения способствует введения правил математических действий, которые на первый взгляд кажутся искусственными. Для их оправдания требуется найти подходящую интерпретацию. Первым примером такого правила является правило нахождения неизвестного слагаемого. Оно оправдывается интерпретацией этой задачи как задачи нахождения длины части отрезка.

Пример 4. Придумайте правило нахождения неизвестного слагаемого x, т.е. a + x = b, где a – известное слагаемое; b – известная сумма.

Для этого представьте, что b = AB, a = AC, x = DC (рис. 22). Изменяйте отрезок АС, заполняя таблицу (см. табл. 3). Придумайте, как найти ВС не измеряя его. Проверьте свои выводы измерениями.

Рис. 22

Таблица 3

Аналогичные задачи могут быть поставлены для организации деятельности учащихся при изучении правил решения других задач на нахождение неизвестного компонента арифметического действия: неизвестного уменьшаемого, вычитаемого, множителя, делимого, делителя.

Активный характер постановки экспериментов аристотелевского типа требует формирования частично-выявленных знаний об экспериментальном методе: введении и раскрытии содержания терминов эксперимент, цель эксперимента, таблица экспериментальных данных, экспериментальное оборудование, план проведения эксперимента, количество испытаний, модель объекта изучения.

Распространение знаний об экспериментальном методе идет в трех взаимосвязанных направлениях:

1) развитие представлений о функциях экспериментальных методов в учебном познании (оправдание, объяснение, разведка, контроль);

2) развитие представлений о видах интерпретационных моделей математических объектов (геометрические, физические, вещественные, аналитические);

3) накопление представлений о частных разновидностях экспериментов и условиях их использования (метод оригами, метод разрезания и складывания, метод измерения, метод наложения, метод взвешивания, метод переливания / пересыпания, численный эксперимент и т.п.).

Содержательной основой для реализации этих направлений выступают вопросы, связанные с изучением различных конструктивных и измерительных инструментов, оперирования с мерными величинами.

Пример 5. Придумайте, как использовать детские качели-качалки (рис. 23) для того, чтобы методом эксперимента:

1) сравнивать массы детей на них качающихся;

2) сравнивать длины плеч самой качели (если они регулируются);

3) решать задачи на определения отношения, в котором точка делит отрезок.

Рис. 23. Детская качель-качалка

Пример 6. Из бумаги вырезаны несколько треугольников (рис. 24).

1) Найдите методом наложения и отметьте стороны, которые у всех этих треугольников равны.

2) Придумайте способ сравнения длин их высот, опущенных на отмеченные стороны, без использования линейки.

3) Придумайте эксперимент, который позволяет сравнить их площади, и показать, что площади таких треугольников равны.

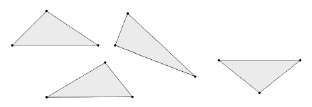
Рис. 24. Равновеликие треугольники

Все выше сказанное позволяет описать развитие линии экспериментальной математики в начальной школе в терминах целей, специфического и неспецифического содержания и результатов обучения (табл. 4).

Таблица 4

Развертывание линии экспериментальной математики
в начальной школе (1–4 классы)

2. Развитие линии экспериментальной математики в основной школе. Основная школа является наиболее важным периодом в развитии линии экспериментальной математики, так как здесь учащимся предстоит не только освоить компьютерное экспериментирование во всем его многообразии, но и осознать ограниченность экспериментального подхода, значимость разумного сочетания экспериментальных методов с теоретическими.

В 5–6 классах учащиеся продолжают экспериментировать с вещественными моделями математических объектов, делают выводы о математических закономерностях, убеждаются в целесообразности вводимых правил математических действий с опорой на различные типы интерпретационных моделей (диаграммы, графики, масштабные и схематичные изображения геометрических фигур, изображение чисел точками числовой прямой, игральная кость, монета, урна с шарами, дерево вариантов и т.п.). Большие возможность для решения этих задач предоставляет линия числа и вычислений в органичном сочетании с мерными величинами и геометрическими фигурами, введение буквенного обозначение числа, пропедевтика функциональных зависимостей, начала комбинаторики и теории вероятностей.

Пример 7. Пусть два игрока играют в такую игру: Точка находится в начале координат. Первый игрок бросает красный игральный кубик и передвигает точку вправо по координатной прямой на столько единиц, сколько выпало на кубике. Затем записывает свой ход, прибавляя к первоначальной координате точки количество выпавших на кубике единиц (например, «5 + 4»). Второй игрок бросает синий кубик и передвигает эту же точку влево по координатной прямой на столько единиц, сколько выпало на его кубике. Затем он также записывает свой ход, вычитая из координаты точки количество выпавших единиц. Выигрывает тот игрок, которому удалось за 10 ходов перетянуть точку на свою сторону координатной прямой. Если точка окажется на положительной полуоси, то выигрывает первый игрок, если на отрицательной полуоси, то выигрывает второй.

1) Сыграйте в эту игру со своим соседом по парте.

2) Повторите игру, но точку при этом не перемещайте. Можно ли узнать, кто победил в игре лишь по записям ходов? Объясните, как.

В 5–6 классах учащиеся должны получить представления об особенностях компьютерного эксперимента (вычислительных в Excel, геометрических в DGS). Об его преимуществах по сравнению с экспериментами на вещественных моделях, об ограниченности компьютерных экспериментов по сравнению с дедуктивными и аналитическими методами.

Пример 8. Зависит ли сумма углов треугольника от его формы? Что покажут эксперименты, в основе каждого из которых лежит один из трех разных методов (метод измерения, метод оригами, компьютерный метод)?

Эксперимент 1 (метод измерения). Нарисуйте на листе бумаги три треугольника: тупоугольный, остроугольный и прямоугольный. Измерьте транспортиром углы каждого и найдите их сумму. Результаты занесите в таблицу (см. табл. 5):

Таблица 5

Сделайте вывод.

Эксперимент 2 (метод оригами). Вырежьте из листа бумаги три треугольника: тупоугольный, остроугольный и прямоугольный. Найдите и отметьте наибольшую сторону каждого. Наметьте сгибанием на отмеченной стороне основание высоты каждого треугольника. Уложите в эту точку все вершины треугольников (рис. 25). Сделайте вывод.

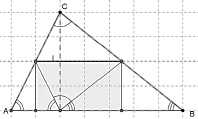
Рис. 25. Складывание треугольника

Эксперимент 3 (компьютерный). Постройте в графическом окне GeoGebra произвольный треугольник, измерьте его углы. С помощью строки ввода создайте величину, равную сумме всех углов. Перемещайте по экрану вершины треугольника и следите за изменением суммы углов. Повторите эксперимент несколько раз, меняя настройки точности измерения. Сделайте вывод. К одинаковым ли выводам привели вас все три эксперимента? Какой из экспериментов позволил получить более надежные выводы? Почему?

Систематическое применение компьютерных экспериментов приводит к постепенному накоплению представлений о ситуациях появления парадоксальных результатов (см. пример 9, подробнее об этом написано в параграфе 2.4), которые порождают мотивационную основу для выявления знаний о причинах ограниченности метода компьютерного эксперимента, его возможностях и ограниченности; для развития знаний в курсе информатики и ИКТ о возможных причинах появления ошибок при проведении компьютерного эксперимента (ошибки процессора, ошибки программы, ошибки модели); для развития знаний в курсе математике о статистических методах обработки экспериментальных данных.

Пример 9. В ходе компьютерного эксперимента была обнаружена ситуация, показанная на рис. 26.

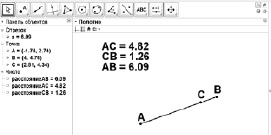
Рис. 26. Ситуация, полученная в ходе компьютерного эксперимента

Какой из выводов является правильным:

1. На отрезке АВ можно найти такое положение точки С, при котором АС + СВ ? АВ.

2. Неравенство АС + СВ ? АВ является следствием неточности измерения.

3. Неравенство АС + СВ ? АВ, является следствием округления данных о величинах отрезков?

С развитием знаний учащихся 7–9 классов, во-первых, о дедуктивном методе и его роли в математике, во-вторых, о месте натурных и модельных экспериментов в естественнонаучном познании, об автоматизированных системах поддержки экспериментальных исследований, начинают складываться обобщенные представления об экспериментальном и теоретическом подходах к исследованию, о видах экспериментов и специфике компьютерных экспериментов. Компьютерный эксперимент предстает перед учащимися, как разновидность модельного эксперимента, отличительной особенностью которого является изучение поведения не вещественной, а математической модели объекта исследования или самого математического объекта в той или иной его интерпретации. Компьютерный эксперимент направлен на получение дискретного конечного набора данных о согласованных значениях двух или большего количества параметров, которые характеризуют поведение модели. Погрешности данных носят систематический (а не случайный) характер и обусловлены особенностями программно-аппаратного комплекса, избранного способа моделирования, степени точности модели.

В этот период содержание в линии экспериментальной математики целесообразно включить лабораторные работы (подробнее в параграфе 3.3). Это облегчит учащимся понимание сходства и различий применения экспериментальных методов в математике и дисциплинах естественнонаучного цикла.

С развитием визуального, логического и абстрактного мышления учащихся ситуации, в которых учащиеся могут отказаться от реального экспериментирования с вещественными или компьютерными моделями математических объектов и перейти к мысленному экспериментированию по канторовскому типу, все более усложняются.

Зарождению представлений о мысленном экспериментировании способствуют ситуации, в которых построение модели является более трудоемким, чем получение данных о результатах экспериментирования с этой моделью, а также ситуации столкновения с неэффективными алгоритмами построения модели.

Пример 10. Придумайте физический эксперимент, позволяющий выяснить, существует ли многоугольник и такая точка внутри него, из которой перпендикуляры, проведенные ко всем его сторонам, попадают только на продолжения сторон.

Решение данной задачи требует доказательства невозможности существования такого многоугольника. В основу может быть положен следующий мысленный эксперимент. Допустим, что такой многоугольник и такая точка внутри него существуют. Представим, что такой многоугольник вырезан из тонкого материала и поставлен на ребро. Так как линия действия силы тяжести не пересекает ребро, то многоугольник перевернется на соседнее ребро. Но, следующее ребро, линия действия силы тяжести снова не пересекает. Многоугольник вновь поворачивается. Так будет продолжаться бесконечно. Таким образом, если такой многоугольник существует, то существует вечный движитель. Вечного движителя не существует, следовательно, не существует и такого многоугольника.

Таблица 6

Развертывание линии экспериментальной математики
в основной школе

Таким образом линия экспериментальной математики в основной школе имеет следующий вид (см. табл. 6).

3. Развитие линии экспериментальной математики в старшей школе. Изучение в старшей школе начал математического анализа создает условия для распространения мысленных экспериментов на новую область, а также для развития представлений учащихся о значимости компьютерных экспериментов в расширении возможностей мысленного экспериментирования.

Благоприятные условия складываются под влиянием необходимости работы с абстракциями актуальной и потенциальной бесконечности.

Как известно, ознакомление с началами математического анализа в старшей школе может быть осуществлено только с опорой на правдоподобные рассуждения и наглядность. Базовая математическая подготовка учащихся недостаточна не только для доказательства теорем математического анализа, но даже и для введения строгих определений фундаментальных понятий: переменной, функции, бесконечности, предела, производной и интеграла. В этих условиях авторы учебников по Алгебре и началам анализа используют методические решения, которые способствуют формированию адекватных представлений об идейной основе математического анализа. Так, например, в учебнике А.Г. Мордковича [58, с. 140], предлагается сопроводить введение определения понятия предела последовательности образами «точки сгущения» для членов числовой последовательности и асимптоты графика функции, заданной на множестве натуральных чисел.

Подобные методические решения создают благоприятные условия для дальнейшего развития линии экспериментальной математики.

По существу, они основаны на использовании эвристических возможностей метода неделимых, опирающегося на идею геометрического атома; метода исчерпывания, неявно апеллирующего к понятию предела; нестрогого метода линейной аппроксимации, исторически предопределивших появление интегральных и дифференциальных методов.

С первыми образцами применения методов, основанных на интуиции бесконечно малой, учащиеся сталкивались уже в основной школе: вывод формул длины окружности и площади круга, установление факта существования иррационального числа, получение формулы для вычисления суммы бесконечно убывающей геометрической прогрессии.

Переход к изучению начал математического анализа создает условия для расширения области применения этих методов, выявления и уточнения смысла используемых математических абстракций.

Так, например, введение понятия предела функции на бесконечности (аналогично, введение понятий предела последовательности, предела функции в точке) может быть предварено постановкой заданий на экспериментальное исследование поведения функции при неограниченном увеличении значения аргумента, на создание визуализаций, иллюстрирующих это поведение.

Пример 11. Исследуйте поведение функции 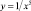при неограниченном увеличении и уменьшении значения аргумента. На этом основании сделайте вывод о значении .

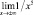Подобные задания довольно распространены в школьных учебниках (например, учебник С.М. Никольского, М.К. Потапова и др. [1]). При этом авторами предполагается, что учащиеся будут проводить исследование, заполняя таблицу соответственных значений. Однако сделать выводы на основе данных, которые учащиеся могут собрать за отведенное время, довольно сложно. В этом случае могут помочь компьютерные расчеты или визуализация процесса перебора значений. Например, они могут проводить наблюдение за изменением координат при перемещении точки по графику функции, неограниченно расширяя наблюдаемую область с помощью инструмента Переместить чертеж (рис 27).

Экспериментирование позволяет учащимся обоснованно отказаться от применения компьютерных инструментов и заменить их математическим инструментом создания образа поведения функции за пределами наблюдаемой области, которым, как известно, является понятие «асимптота».

Несколько экспериментов, подобных представленному на рис. 27, приведут учащихся к обнаружению общего правила отыскания уравнения горизонтальной асимптоты: y = k, где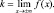

Аналогичным образом, при рассмотрении вопроса о пределе функции в точке могут быль сформированы представления о непрерывности функции в точке и видах разрывов функции, а также обнаружено аналитическое условие существования вертикальных асимптот.

В некоторых случаях компьютерный эксперимент выступает не столько условием, облегчающим проведение правдоподобных рассуждений и мысленного экспериментирования, сколько условием выхода за пределы возможностей, предоставляемых образами. Например, в случаях, когда вывод о предельном значении нужно сделать относительно функции неизвестного вида (I и II замечатель-
ные пределы).

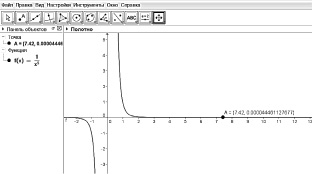
Рис. 27. Рабочий динамический лист для наблюдений

Пример 12. В точке x = 0, как известно, не определены функци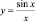и и 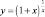. Экспериментально установите поведение каждой функции при приближении значения аргумента к нулю. На этой основе сформулируйте гипотезу о существовании и значении предела каждой из этих функций в точке 0.

Наиболее естественно для учащихся провести эксперимент по аналогии с тем, что был представлен в примере 11. Перемещая точку по графику, легко убеждаемся, что в момент, когда x = 0, точка с экрана пропадает. При этом видим, что график функции кажется непрерывным в этой точке, приближаясь слева и справа, к конкретному значению (рис. 28).

Этот факт является основанием для выдвижения гипотез о существовании пределов данных функций в точке x = 0 и о том, что 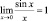и 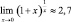. Выводы относительно первого замечательного предела могут быть верифицированы учащимися посредством эксперимента, основанного на геометрической интерпретации исследуемого выражения (рис. 29).

Компьютерный эксперимент может быть использован и для распространения ранее изученных понятий на новые объекты. Например, для введения понятия касательной к графику функции.

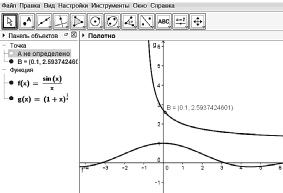
Рис. 28. Рабочий динамический лист
для определения значений I и II замечательных пределов

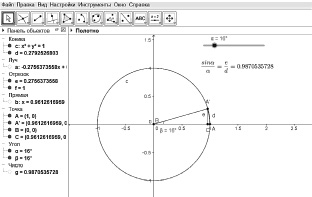
Рис. 29. Рабочий динамический лист
для верификации значения I замечательного предела

Пример 13. На динамическом чертеже изображена окружность с и отмечена точка А на ней. Проведите касательную к окружности через эту точку. Меняя значение параметра а, исследуйте, зависит ли и как, взаимное расположение построенной прямой от вида коники. Уточните условия существования этой прямой.

Результат выполнения этого задания представлен на рис. 30.

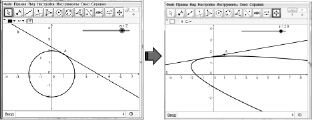
Рис. 30. Результат выполнения задания

Возможность применения инструмента «касательная» к построению касательных к кривым, не являющимся кониками, подсказывает учащимся направление дальнейшего обобщения данного понятия. Мотивационной основой такого обобщения является необходимость обращения к идее линеаризации, позволяющей заменить вопрос об исследовании локальных свойств функции (свойств функции в точке) вопросом об исследовании глобальных свойств касательной, проведенной к графику функции в данной точке. Ситуация, приводящая учащихся к необходимости обращения к данной идее, может возникнуть, например, при постановке следующей задачи.

Пример 14. Пользуясь представленным на динамическом чертеже графиком движения автомобиля, найдите момент времени, в который его скорость впервые превысила допустимую скорость для движения по прилегающей территории – норму 6 км/ч.

Системы динамической математики позволяют создавать динамические визуализации для сопровождения рассуждений и аналитических выкладок в ходе вывода формул, апеллирующих к понятию предельного перехода. Такая необходимость, например, возникает при решении задачи о нахождении уравнения касательной. Образ касательной для этого должен быть соотнесен с образом секущей графика функции и осмыслен как ее предельное положение.

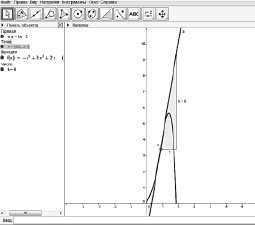
Рис. 31. Динамическая визуализация

Пример 15. Мы можем, пользуясь инструментом «Касательная», построить касательную к графику любой функции в выбранной точке и увидеть на панели объектов уравнение этой касательной. Однако хотелось бы иметь возможность получать уравнения касательных без помощи компьютера. Для этого нужно получить формулу, описывающую зависимость координат точек касательной от формулы, задающей функцию f (x), и координат точки касания A (x0; f (x0)).

Для вывода этой формулы поступим следующим образом. На динамическом чертеже построим график функции f (x). Отметим на нем
A (x0; f (x0)). Придадим аргументу x0 малое приращение ?x. Это позволит нам получить еще одну точку A? (x0 + ?x; f (x0 + ?x)). Теперь вместо задачи о нахождении уравнения касательной, мы можем решить хорошо знакомую нам задачу о разыскании уравнения секущей графика функции, заданной двумя точками А и А?.

Решая систему уравнений:

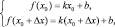
получаем:

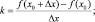
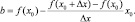
Будем уменьшать заданное приращение ?x. Для того, чтобы увидеть, как это влияет на изменение положения секущей АА? построим динамический чертеж, на котором ?x задано с помощью инструмента «Ползунок» и принимает значения из промежутка [0; 1], c шагом 0,0001 (рис. 32).

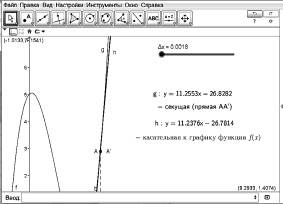
Рис. 32. Динамическая визуализация к выводу формулы

Видим, что секущая осуществляет поворот вокруг точки А, постепенно приближаясь к положению, занимаемому касательной. Обозначим предел отношения 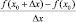при ?x ? 0 символом f ?(x0). Уравнение касательной примет вид:

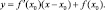
Компьютерные эксперименты при изучении начал математического анализа в школе целесообразно использовать не только для демонстрации новых возможностей инфинитезимальных методов и идей
математического анализа, лежащих в основе современных представлений о дифференциальном и интегральном исчислении, но для формирования представлений о недостаточной строгости их описания.

Пример 16. Разрешите софизм: «Если треугольники имеют хотя бы одну пару равных сторон, то их площади равны».

Доказательство (методом неделимых). Представим, что каждый из данных треугольников состоит из отрезков, параллельных сторонам АВ и DE, таким, что АВ = DE (рис. 33). Длины отрезков, которые заполняют эти треугольники, пробегают все значения от 0 до АВ = DE. Следовательно, для каждого отрезка из треугольника АВС, найдется равный ему в треугольнике DFE. Площадь треугольника равна сумме длин отрезков, которые его заполняют, следовательно, площади треугольников равны как суммы, состоящие из попарно равных слагаемых. Что и требовалось доказать.

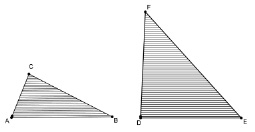
Рис. 33. Динамическая визуализация парадоксов метода неделимых

Важным элементом развития представлений учащихся о значении компьютерных экспериментов в математике является постановка аналитически неразрешимых задач на уровне общего образования.

К числу таких задач относится интересный для учащихся вопрос о раскрытии неопределенностей, который вытекает из обсуждения причин запрета деления на ноль, о сравнении бесконечно малых, скоростей изменения функций и т.п.

Пример 17. Расположите данные функции в порядке убывания скорости их возрастания на плюс бесконечности: y = x, y = x3, y = x10, y = 2x.

Сначала задача кажется учащимся не сложной, так как для решения вопроса о сравнении скоростей изменения пар функций y = x и y = x3, y = x и y = x10, y = x и y = 2x, достаточно найти их производные и сравнить их значения при x ? ?. Чуть сложнее решение задачи для пары y = x и y = x10. Здесь нужно догадаться о возможности рассмотрения отношений функций и выработать новый критерий: «Пусть даны две бесконечно большие на + функции f(x) и g(x) одного знака. Если 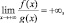то f(x) имеет более высокий порядок роста, чем g(x). Если 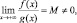то функции имеют одинаковый порядок роста. Если 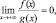то функция g(x) имеет более высокий порядок роста». Однако во всех этих случаях ответ может быть получен учащимися аналитически. Сравнение скоростей изменения пар функций y = x10 и y = 2x; y = x3 и y = 2x является для них аналитически неразрешимой задачей. В этом случае естественным будет обращение к компьютерному эксперименту (рис. 34 и 35).

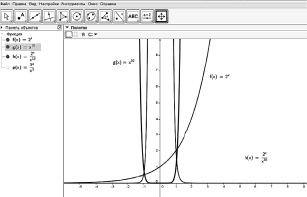
Рис. 34. Компьютерный эксперимент для решения задачи
о сравнении скоростей изменения первой пары функций

Вывод может быть получен на основе чтения графиков отношений этих функций с опорой на предположение, что поведение графиков за пределами области наблюдения сохраняется.

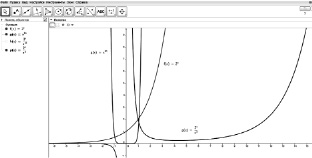
Рис. 35. Компьютерный эксперимент для решения задачи
о сравнении скоростей изменения второй пары функций

На старшей ступени общего образования развиваются знания учащихся и о модельных экспериментах в математике. В их перечень включаются статистические эксперименты, идеи стохастического моделирования и метод Монте-Карло.

Пример 18. Дан отрезок ОЕ, равный единице. Оцените вероятность события, состоящего в том, что две случайно выбранные на отрезке ОЕ точки разобьют его на части, из которых можно будет составить треугольник.

Решение задачи может быть начато с использования статистического способа оценки вероятности, который опирается на данные компьютерного эксперимента (рис. 36).

В качестве счетчика благоприятных исходов опыта задается функция Если[периметрмногоугольник1?1?периметрмногоугольник3?1,1,0].

Результаты статистического эксперимента позволяют выдвинуть гипотезу о том, что вероятность приблизительно равна 1/4.

Для аналитического обоснования справедливости выдвинутой гипотезы учащимся необходимо обнаружить иную интерпретацию опыта, описанного в условии задачи.

Рассмотрим случайное событие А = «из полученных отрезков можно составить треугольник». Совместим точку О отрезка с началом координат оси Х, тогда координата точки Е равна 1. Мы можем рассмотреть отрезок [0; 1].

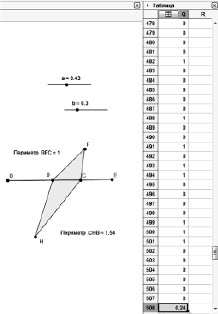
Рис. 36. Компьютерный статистический эксперимент
для решения задачи об оценке вероятности существования треугольника

Опыт состоит в том, что отрезок [0; 1] случайным образом делят на три части. Это равносильно случайному выбору двух точек на отрезке [0; 1]. Координату левой точки В обозначим х, а правой точки С – у (см. рис. 37).

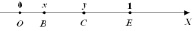
Рис. 37

Таким образом, множество точек (х; у) задается системой:

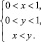
Данная система определит треугольник площадью S, который является областью всевозможных исходов опыта (рис. 38).

Треугольник из полученных трех отрезков можно составить, если каждая сторона меньше суммы двух других сторон (неравенство треугольника). Следовательно, координаты точки (х; у) должны удовлетворять условиям:

Построим фигуру, описанную системой неравенств средствами GeoGebra. Она представляет собой треугольник площадью s, который изображает множество благоприятных исходов опыта (см. рис. 38).

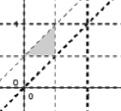
Рис. 38

Полученное изображение позволяет оценить вероятность интересующего события с использованием геометрического способа:

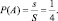
Курс стереометрии также представляет массу возможностей для развития знаний учащихся об экспериментальных методах. В силу ограниченности познавательных функций статических проекционных изображений, изучение стереометрии осуществляется с применением вещественных моделей, а также компьютерных динамических моделей геометрических фигур.

Пример 19. Постройте сечение куба плоскостью, проходящей через точки К, F и L. Исследуйте зависимость вида сечения от положения данных точек на ребрах куба.

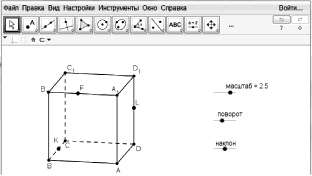
Рис. 39. Рабочий динамический лист для решения задачи
на построение сечений куба и его исследования

Проведение экспериментов с использованием проекционных динамические моделей (рис. 39) требует от учащихся знания свойств, сохраняемых и не сохраняемых проекционных чертежом, а также использования возможностей изменения ракурса изображения, введения дополнительных построений и построения развертки для «настройки» проекционных изображений по заданным метрическим свойствам геометрических фигур, получения данных об этих свойствах в ходе компьютерного эксперимента.

Таким образом, линия экспериментальной математики в старшей школе имеет следующий вид (табл. 7).

Таблица 7

Развертывание линии экспериментальной математики в старшей школе

Представленное описание содержательно-методической линии экспериментальной математики, не претендует на полноту. Оно призвано лишь наметить и проиллюстрировать примерами основные ориентиры ее развертывания в содержании базовых математических курсов по ступеням общего образования.

Отметим лишь, что данная линия с полным правом относится к методологической составляющей математического образования, что определяет необходимость реализации при ее проектировании следующего набора принципов [96].

Принцип функциональной значимости – включение в школьный курс лишь тех знаний об использовании экспериментального подхода в математике, которые значимы для ее изучения (в соответствии с идеями исследовательского обучения в математике)

Принцип функциональной полноты – включение в школьный курс такого комплекса знаний об экспериментальном подходе в математике, который обеспечит готовность учащихся к саморегуляции деятельности по использованию экспериментальных методов в рациональном сочетании с теоретическими.

Принцип предметной обусловленности – использование для развития содержания линии тех возможностей, которое предоставляет методика обучения содержанию основных линий школьного курса математики.

Принцип комплексности источников – использование в качестве источников содержания линии образцов реализации экспериментального подхода к математике, которые предоставляются научными данными, опытом деятельности создателей учебников и учителей.