Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

2.3. Методические особенности организации исследовательского обучения математике в модели «Экспериментальная математика» на разных этапах обучения

В данном параграфе, мы остановимся на организационно-деятельностных условиях, которые, по нашему мнению, обеспечат постепенное становление качеств математика-экспериментатора.

Эти качества должны обеспечивать учащимся ту степень самостоятельности в исследовательской деятельности, которая определена Х. Банчи и Р. Беллом [109] для различных уровней исследовательского обучения и позволять учащимся выход в зону ближайшего развития их исследовательской компетентности.

Х. Банчи и Р. Белл в своем исследовании отмечают, что на первом уровне – уровне конфирматорного исследования – учитель должен продемонстрировать учащимся образец решения исследовательской задачи или предъявить результат исследования ученых в готовом виде, организуя их деятельность по сбору подтверждающих этот результат фактов, конструированию примеров и контрпримеров. На втором уровне – уровне проведения исследований по плану учителя – учитель должен поставить перед учащимися задание на проведение исследования по готовому плану, инструкции или направлять учащихся в исследовании с помощью указаний.

На третьем уровне – уровне проведения исследований под руководством учителя – должен быть организован сократовский диалог/полилог с учащимися, вовлекающий их в деятельность постановки исследовательской задачи на основе уточнения условий поиска ответа на вопрос учителя, разработки и реализации замысла ее решения, оценки полученных результатов. На четвертом уровне – уровне свободных исследований – учащиеся сами ставят исследовательские вопросы, планируют ход поиска ответов на них, оформляют и представляют результаты, учитель выступает при этом в роли более опытного партнера, предлагая альтернативные стратегии деятельности, но, не отвергая стратегий учащихся.

Описанный авторами характер взаимодействия учителя и учащихся на разных уровнях исследовательского обучения позволяет осмыслить уровневую модель организации исследовательского обучения с позиции теории Л.С. Выготского [31] о связи обучения с зонами психического развития. Положения этой теории позволяют описать каждый уровень исследовательского обучения с точки зрения достигнутых результатов формирования опыта исследовательской деятельности (зона актуального развития) и тех результатов, на достижение которых должны быть направлены обучающие воздействия (зона потенциального развития). Они представлены в табл. 8.

Достижение образовательных результатов, находящихся в зоне ближайшего развития, как было показано Л.С. Выготским, обеспечивается вовлечением учащихся в исследовательскую деятельность, которую они осуществляют с помощью учителя. При этом помощь должна быть дозирована и адекватна поставленным образовательным задачам.

Остановимся более подробно на тех методах и средствах, которые могут быть использованы учителем для оказания помощи учащимся в исследовательской деятельности на разных уровнях исследовательского обучения в стиле экспериментальной математики.

Одним их специфических средств являются рабочие динамические листы – электронные образовательные ресурсы, созданные средствами систем динамической математики и допускающие активность пользователя по отношению к контенту. Рабочие динамические листы могут иметь различное устройство, которым определяется уровень допустимой активности пользователя. Это позволяет классифицировать их по уровням интерактивности.

В своем изложении мы будем придерживаться общей шкалы уровней интерактивности электронных образовательных ресурсов, предложенной А.В. Осиным:

1 уровень – условно-пассивные формы деятельности.

«Сценарий воспроизведения контента предусматривает лишь простейшие реакции, повышающие комфортность восприятия и управления. Такой контент нельзя называть интерактивным: пользователь лишь выбирает фрагмент для усвоения, но не оперирует с его элементами» [68, с. 68]. Примерами ЭОР, разработанных на базе систем динамической геометрии, и относящихся к данному уровню являются анимированные изображения и линейные манипуляторы. Главным назначением таких динамических листов в исследовательском обучении является визуализация закономерности, выявленной в ходе исследования, представление работы с образом объекта, которая привела к получению результата, наведение на обнаружение ситуации, мотивирующей к поиску доказательства. Таким образом, динамические листы этого уровня интерактивности мы рекомендуем использовать на уровне конфирматорного исследования.

Таблица 8

Зоны актуального и потенциального развития опыта исследовательской деятельности учащихся, отнесенные к различным уровням исследовательского обучения

2 уровень – активные формы деятельности.

Данный уровень характеризуется простым взаимодействием пользователя с контентом на уровне элементарных воздействий/откликов. К активным формам автор относит следующие: множественный выбор, вращение объемных тел, изменение угла зрения, активизация различных элементов композиции по выбору пользователя, изменение состава, компоновки элементов и др. К ЭОР данного уровня интерактивности, разработанным на базе систем динамической геометрии, можно отнести нелинейные манипуляторы. Примером нелинейного манипулятора предназначенного для целей исследовательского обучения может служить динамический лист с системой подсказок, которым по желанию может воспользоваться учащийся на различных этапах исследования. Нелинейный манипулятор мы относим к уровню исследований, проводимых по плану учителя, так как большая степень самостоятельности учащихся в исследовании делает невозможным предварительное задание системы подсказок.

3 уровень – деятельностные формы.

Деятельностные формы «характеризуются конструктивным взаимодействием пользователя с учебными объектами/процессами по заданному алгоритму с контролем отклонений» [68, с. 69]. Деятельностные формы, как отмечает А.В. Осин, отличаются от активных форм тем, что создают у пользователя иллюзию свободы действий. Предоставляют ему право самостоятельно принимать решения, связанные с планированием деятельности, выбором средств реализации плана. Однако свобода пользователя ограничена набором предоставленных ему инструментов. Они заданы таким образом, что каждый шаг, не позволяя отклоняться от цели, ведет к единственно верному решению, и путь решения учебной задачи предопределен. Ярким представителем ЭОР этого уровня интерактивости являются интерактивные чертежи, в которых ограничен набор инструментов, доступных пользователю. Динамические листы этого уровня интерактивности хороши для организации исследовательского обучения на третьем уровне, так как они не содержат прямых указаний относительно характера деятельности учащихся, лишь направляя ее, создавая иллюзию самостоятельного и свободного принятия решений.

4 уровень – исследовательские формы.

«Исследовательские формы взаимодействия с контентом характеризуются возможностью получения множества комбинаций / состояний объектов / процессов, в том числе – не определенных заранее. Пользователь манипулирует представленными или сгенерированными в процессе взаимодействия с ЭУМ объектами и процессами. Учебные цели не внедрены в контент, т.е. пользователю не навязывается последовательность действий, которая заведомо приведет к заданному результату. На любом шаге позволяется сделать любой выбор и далее производить следующие шаги до получения некоторого результата. При этом ни один выбор не квалифицируется как неверный» [68, с. 70]. Этот уровень интерактивности по нашему мнению, может быть представлен готовыми динамическими чертежами (шаблонами многогранников, развертками и т.п.), которые каждый учащийся может использовать по своему усмотрению.

Безусловно, готовый динамический чертеж несколько ограничивает исследовательскую свободу пользователя, так как он обладает уже заданным характером динамики и способом контроля изменений. Между тем работа с самой средой позволяет поддерживать практически все этапы цикла, все этапы учебного математического познания при реализации исследовательского подхода к обучению.

Таким образом, можно говорить о возможности установления соответствия между уровнями интерактивности рабочих динамических листов, создаваемых средствами систем динамической математики, и уровнями исследовательского обучения математике (см. табл. 9).

Представленные виды рабочих динамических листов являются средствами помощи, имеющими невербальный характер. Кроме них на разных уровнях исследовательского обучения применимы и средства, оговоренные в самой модели Х. Банчи и Р. Белла. Для первого уровня – это инструкции и указания по выполнению исследовательских действий практического характера. Для второго уровня – планы хода исследования, представленные перечнем шагов решения, серией вспомогательных задач и т.п. Для третьего уровня – методической схемой построения сократовского диалога или полилога. На четвертом уровне – тематикой консультаций с научным руководителем, вопросов для обсуждения на семинарах.

Остановимся на описании специфики сократовского метода построения беседы как наиболее трудного для практической реализации и наиболее ценного с точки зрения развивающих воздействий.

Основу сократовского метода построения беседы составляет восходящее к Сократу убеждение, что процесс приобретения истинного знания человеком – это процесс рождения этого знания в самом человеке. Именно поэтому, как утверждают ученые [47], сам Сократ называл этот метод ведения диалога «майевтикой» – повивальным искусством. Сегодня термин «майевтика» применяется для обозначения ключевых приемов ведения сократовского диалога/полилога:

– «Положительная майевтика» – демонстрация непонимания, побуждающая собеседника к конкретизации (детализации) или обобщению высказанных положений.

– «Деструктивная майевтика» – демонстрация непонимания, побуждающая собеседника к переоценке и корректировке своих позиций, к переосмыслению высказанных положений.

Таблица 9

Классификация рабочих динамических листов и рекомендации
по их использованию в исследовательском обучении

Наряду с этими приемами при ведении сократовского диалога используются такие приемы как «ирония» и «агон». Они выполняют те же функции, что и положительная и деструктивная майевтики соответственно, но имеют более прямолинейный характер: прямая критика представленного способа изложения позиции, прямое противоречие высказанной позиции.

Структуру сократовского метода беседы мы представили следующей обобщенной методической схемой (см. табл. 10).

Таблица 10

Методическая схема построения сократовского диалога/полилога

Данная схема показывает, что сократовский метод построения беседы (или каждый его виток) состоит из трех этапов. Первые два этапа отнесены к уровню актуального развития субъектного опыта учащихся и предназначены для того, чтобы актуализировать его, побудить его к вербализации, конкретизации (детализации) и обобщению. Третий этап имеет целью вывести собеседника в зону ближайшего развития за счет демонстрации искусственности барьеров, созданных опытом.

Проиллюстрируем теперь все описанные средства помощи конкретными примерами методики работы с задачей на различных уровнях исследовательского обучения в стиле экспериментальной математики.

1. Уровень конфирматорного исследования

Пример 1. Изучение теоремы о площади круга (8 класс).

Выбор первого уровня реализации исследовательского обучения определен следующей ситуацией (см. табл. 11):

На этапе постановки задачи учитель представляет учащимся проблему поиска квадратуры круга. Здесь целесообразно актуализировать их знания об известных формулах вычисления площадей фигур в логике их изучения, а также напомнить учащимся, что все они получены с использованием метода квадратур, основанного на теореме о равновеликости равносоставленных планиметрических фигур.

Таблица 11

На этапе обоснования необходимости перехода к компьютерному эксперименту полезно организовать деятельность учащихся по проверке формулы площади круга с помощью эксперимента, связанного с разрезанием вырезанного из бумаги круга на сектора и складыванию из них модели параллелограмма или прямоугольника (рис. 40). Погрешность, которую они получат при измерении и вычислении, станет достаточным основанием для обращения к компьютерному эксперименту.

Рис. 40. Результат замены круга равновеликой фигурой для сведения вопроса о вычислении его площади к вопросу о вычислении площади прямоугольника

Этапы планирования компьютерного эксперимента и разработки средств для его проведения целесообразно реализовать в форме представления учащимся готового рабочего динамического листа (рис. 41) и рассказа учителя об идее метода исчерпывания со ссылкой на Евдокса Книдского.

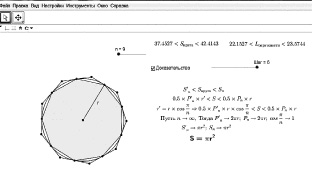
Рис. 41. Линейный манипулятор
для представления вывода формулы площади круга

Для организации деятельности учащихся по сбору и анализу данных может быть поставлено задание на поиск значения n, начиная с которого площадь круга может быть определена с заданной точностью (до целых, десятых, сотых и т.п.). На этапе использования результатов компьютерного эксперимента учащимся можно предложить прокомментировать доказательство теоремы по его представленной динамической записи.

В представленном примере активность учащихся ограничена проведением модельных экспериментов двух типов: компьютерного и модельного (с вещественной моделью). Оба эти эксперимента направлены на верификацию утверждения, предъявленного в готовом виде, и обеспечение понимания идейного сходства и различия метода квадратур и метода исчерпывания.

Пример 2. Методика работы с теоремой о сумме углов треугольника (7 кл.).

Причины выбора первого уровня организации исследовательского обучения сходны с указанными в предыдущем примере (см. табл. 12).

Таблица 12

Однако здесь имеется возможность вовлечь учащихся в деятельность не только по проведению компьютерного эксперимента, но и по созданию динамической модели, а также средств фиксации данных эксперимента.

Мотивационной основой для поиска свойства суммы углов треугольника может служить задача на оценку возможности определения вида треугольника, если известно соотношение его углов, например: 1:2:3. На этапе докомпьютерного решения данной задачи можно попросить учащихся попросить подобрать опорные углы так, чтобы в результате получался: остроугольный, прямоугольный и тупоугольный треугольник. Для проверки существования треугольников с выбранными углами учащимся предлагается выполнить компьютерные построения по инструкции (см. табл. 13).

Обобщая и уточняя объяснения учащихся, учитель формулирует теорему и просит использовать изготовленный ресурс для проверки этого утверждения. С этой целью нужно лишь дополнительно создать вычисляемую переменную – сумму углов треугольника с помощью строки ввода. Затем учитель предъявляет одно из доказательств теоремы и организует работу учащихся по поиску других способов доказательства в литературе.

Таблица 13

Построение треугольника

2. Уровень проведения исследований по плану учителя.

Пример 3. Методика работы на занятии кружка с исследовательской задачей: «Лестница вертикально стоит возле стены. На нее забрался котенок. Вдруг лестница начала соскальзывать. Установите, зависит ли траектория движения котенка, не перемещающегося по лестнице, от места его положения на лестнице. Если да, то как?»

Методику работы с данной задачей мы отнесли ко второму уровню исследовательского обучения в связи со следующими соображениями (см. табл. 14).

Таблица 14

Данная задача имеет сюжетную постановку. Для перевода ее на язык математики полезно включить учащихся в деятельность проигрывания ситуации, описанной условием задачи. Для моделирования ситуации учащиеся используют картонную коробку, из которой вырезают трехгранный угол. Лестницу изображает карандаш, а котенка – кусок пластилина, к которому прикреплен еще один небольшой карандаш так, чтобы при движении лестницы он вычерчивал на задней стенке траекторию движения котенка. Проигрывание ситуации создает у учащихся образ, на основе которого учитель вводит понятие геометрического места точек (ГМТ), рассказывает о способах задания ГМТ, раскрывает смысл требования «Найти ГМТ». Все это необходимо для осмысления учащимися заданной ситуации как математической задачи и предъявления учащимся плана исследования:

1. Создать динамическую модель задачной ситуации, зависящую от двух параметров: с – высота расположения верхней части лестницы (меняется от 0 до l, где l – выбранная длина лестницы); k – величина части лестницы от верхнего ее края до места расположения котенка.

2. Провести серию экспериментов по исследованию зависимости формы ГМТ от места положения котенка. Для формулировки гипотезы определить вид кривой, являющейся искомым ГМТ, используя инструмент «Коника по пяти точкам».

3. Собрать в сети Интернет информацию о способах задания кривых данного вида.

4. Использовать информацию для описания зависимости ГМТ от k уравнением кривой.

5. Постановить новые задачи, развивающие идею решенной.

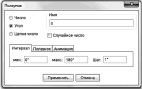
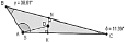
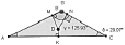
Помощь учащимся в реализации данного плана может оказать нелинейный манипулятор (рис. 42). Если ученик не может самостоятельно создать динамическую модель ситуации или хочет проверить себя, то он может вывести на экран готовую модель, отобразить вспомогательные элементы модели или протокол построения. Если ученик затрудняется в получении уравнения кривой, то он может вывести на экран Аналитическое решение и исследовать последовательность производимых шагов/действий. Если затрудняется в формулировке гипотезы или результата исследования, то он выводит на экран готовый результат.

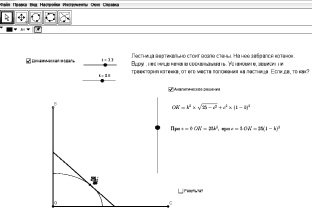
Рис. 42. Нелинейный манипулятор с подсказками к решению задачи

Все эти средства помощи учащимся могут быть дополнены прямыми указаниями учителя или наводящей системой вопросов. Необходимость этих дополнительных воздействий наиболее вероятна на этапе выбора теоретических оснований получения уравнения и их применения к конкретной ситуации.

3. Уровень проведения исследований под руководством учителя.

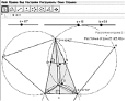
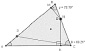
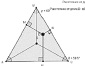
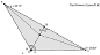
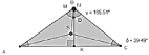
Пример 4. Методика работы на занятии кружка с исследовательской задачей: «На необитаемый остров, имеющий форму правильного треугольника, каждая сторона которого представляет собой пляж, попали двое. Питер, занимаясь сбором моллюсков, хочет построить хижину так, чтобы суммарное расстояние до всех трёх пляжей было минимально. Майкл проводит всё время на мысах (в вершинах треугольника) в ожидании спасительного корабля. Он хочет построить хижину так, чтобы суммарное расстояние до мысов было минимально. Где каждому из них нужно построить хижину? Существует ли на таком острове место для их общей хижины? Зависит ли результат решения задачи от формы острова? Если да, то как?».

Возможность реализации исследовательского обучения третьего уровня при работе с данной задачей определяется следующей ситуацией (см. табл. 15).

Таблица 15

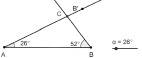
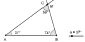
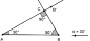
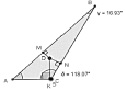
На данном уровне для оказания помощи учащимся используется сократовский метод построения беседы и рабочий динамический лист с ограниченным набором инструментов (рис. 43).

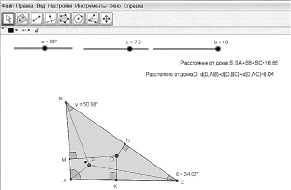
Рис. 43. Рабочий динамический лист для проведения эксперимента с ограниченным набором инструментов

Выбор параметров, задающих треугольник, ориентирует учащихся в выделении значимых условий для исследования зависимости. Готовый динамический чертеж снимает трудности учащихся, связанные с заданием отрезков, изображающих расстояние от точки внутри треугольника до его сторон. Оставленные инструменты ориентируют в поиске способа построения точки Торричелли, а также в исследовании свойств второго ГМТ.

В рамках данного примера на первом этапе работы с задачей учащиеся должны преодолеть психологические трудности, связанные с осмыслением поставленных вопросов в сюжетной задаче как вопросов математической задачи на нахождение геометрических мест точек и с исследованием зависимости виды ГМТ от параметров, задающих треугольник. Результат решения первоначально кажется учащимся очевидным – центр равностороннего треугольника (центры вписанной и описанной окружностей для треугольников других видов). Однако требуется более глубокое осмысление задачи через преодоление психологических трудностей. С этой целью учитель использует сократовский метод построения беседы (в форме полилога), методическая схема которого представлена ниже в табл. 16.

Таблица 16

Методическая схема сократовского метода построения беседы
(в форме полилога)

На этапе сбора данных компьютерного эксперимента и получения выводов учащихся подстерегают трудности, связанные с осмыслением понятия «расстояние от точки до отрезка», а также с отказом от первоначальной гипотезы о единственности точки, сумма расстояний от которой до сторон треугольника является наименьшей. Для снятия этих затруднений вновь можно обратиться к организации, теперь уже индивидуальной беседы (диалога) по схеме сократовского метода (см. табл. 17).

Таблица 17

Организация индивидуальной беседы (диалога)
по схеме сократовского метода

На этапе послекомпьютерного решения сократовский метод используется:

– для подведения учащихся к необходимости доказательства выдвинутых гипотез;

– в поиске способа проведения доказательства.

Наличие двух последовательных целей требует реализации на этом этапе двух циклов сократовской беседы. Первый направлен на то, чтобы зародить у учащихся сомнения в полноте и согласованности экспериментальных данных, а второй на то, чтобы навести их на идею использования метода площадей. Представим пример первого цикла (см. табл. 18).

Таблица 18

Подведение учащихся к необходимости доказательства
выдвинутых гипотез

Сократовский диалог на этапе развития идеи задачи применяется для оказания помощи учащимся в определении направлений дальнейших исследований за счет частичного видоизменения задачной ситуации. В данном случае он направлен на оказание помощи учащимся в выделении свойств треугольников, значимых для изменения вида ГМТ (см. табл. 19).

Таблица 19

Сократовский диалог на этапе развития идеи задачи

В заключение заметим, что наиболее типичными целями применения сократовского метода при работе с задачей экспериментальной математики являются:

– переосмысление гипотез, выдвинутых под влиянием экспериментов, проводимых вручную;

– переоценка степени убедительности результатов эксперимента;

– преодоление ограниченности привычных поисковых стратегий и базовых знаний.

4. Уровень свободных исследований.

Рассмотрим организацию помощи учащимся на этом уровне на примере исследования, являющегося продолжением рассмотренной выше задачи о строительстве хижин (см. табл. 20). Данная работа получила диплом третьей степени на конкурсе «Математика и проектирование» в 2015 году.

Для подготовки учащегося к систематизации данных компьютерного эксперимента учитель организует подготовительный семинар, на котором представляет особенности решения алгебраических и геометрических задач с параметрами, вводит понятие контрольной оси,
критических значений параметра, демонстрирует образцы решения задач и записи результатов решения. В заключении предлагает осмыслить возможность рассмотрения исследовательской задачи как геометрической задачи с параметрами.

Таблица 20

Организация помощи учащимся на этом уровне

Результаты своих размышлений учащийся представляет на следующем семинаре. Здесь же представляются результаты компьютерных экспериментов, уточняется и обосновывается набор критических значений параметров. Создается схема систематизации данных экспериментов (рис. 44 и 45).

Рис. 44. Результаты компьютерного эксперимента для определения ГМТ,
сумма расстояний от которых до вершин треугольника наименьшая

Рис. 45. Результаты компьютерного эксперимента для определения ГМТ,
сумма расстояний от которых до сторон треугольника наименьшая

Следующий этап исследования – это оценка степени новизны полученных результатов. Учащемуся предлагается найти в Интернет информацию, касающуюся постановки и решения сходных задач и представить ее на семинаре. Результатом сбора данных является историко-научное сообщение о теореме Вивиани и теореме Б. Кавальери, П. Ферма, Э. Торричелли, Т. Симпсона, Ж. Бертрана: вклад ученых, доказательство, построение точек. Результатом семинара является выделение недоказанных ранее утверждений (рис. 46).

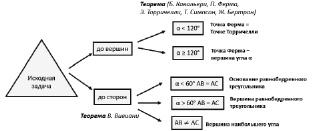
Рис. 46. Схема выделения части недоказанных утверждений

Результаты поиска учащимся способа доказательства оставшихся утверждений также обсуждаются на семинаре или целой серии семинаров.

Завершающий семинар – это предзащита исследовательской работы.

Таким образом, учащийся имеет возможность обсудить с научным руководителем, другими учащимися и специалистами, присутствующими на семинаре, результаты каждого этапа исследования, а также получить задания для его продолжения (см. табл. 21).

Таблица 21

Этапы гносеологического цикла экспериментальной математики

В заключение хотелось бы отметить, что описанными в параграфе педагогическими сценариями не описывается все многообразие способов реализации модели исследовательского обучения в стиле экспериментальной математики. Опыт применения модели, накопленный участниками Российско-Болгарского проекта «Методики и информационные технологии в образовании», будет представлен в третьей главе.