Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

2.4. Эффекты и риски исследовательского обучения в стиле экспериментальной математики

В этом параграфе мы хотим, во-первых, обозначить основные эффекты и риски, связанные с применением предлагаемой нами модели исследовательского обучения математике в условия образовательной практики, а, во-вторых, опираясь на опыт учителей-экспериментаторов Российско-Болгарского проекта «Методики и информационные технологии в образовании» [144], дать некоторые рекомендации по профилактике возникновения этих рисков.

2.4.1. Формирование опыта исследовательской деятельности в области математики и риск деформации исследовательского стиля

Исследовательское обучение в стиле экспериментальной математики позволяет целенаправленно формировать у учащихся опыт математика-экспериментатора. Основой для этого служит широкое вовлечение учащихся в деятельность проверки существования математических объектов с заданными свойствами, построением их виртуальных моделей; установления свойств, инвариантных относительно заданной динамики изменения параметров модели; исследования характера зависимости одних свойств модели от других; контроля аналитических выкладок компьютерными расчетами; верификации выдвинутых гипотез экспериментальными данными, постановки новых задач на базе решенных, модификацией исследовательской модели.

Однако при освоении экспериментального подхода в отрыве от теоретического возникает риск деформации стиля математического мышления учащихся.

Экспериментальный подход к познанию окружающего мира является врожденным, реализация представленных возможностей лишь переносит его в область математических абстракций, но не обогащает теоретическим подходом. Более того, нами установлено, что его привлекательность настолько сильна, что даже учителя математики с большим стажем работы быстро отказываются от применения более трудных теоретических методов при собственном решении задач и объяснении нового материала школьникам.

Для снижения данного риска, по нашему мнению, желательно насытить школьную программу задачами, решение которых делает экспериментальный поиск бесполезным, или требует привлечения теоретических соображений для его реализации. Приведем примеры таких задач.

Пример 1. Существуют ли нетождественные нулю функции, композиция которых тождественна нулю? Если существуют, то каковы ориентиры для подбора таких пар функций?

Решение данной задачи начинается с перебора пар известных функций, т.е. с мысленного эксперимента. Результатом этой работы является обнаружение примеров, положительно решающих вопрос о существовании. Например, y = [x] и y = {x}. Следующий этап – это попытки сконструировать для каждой известной функции парную известными учащимся способами: сужением естественной области определения или созданием кусочно-заданной функции. Результатом этой работы является обнаружение функций, для которых сконструировать парную функцию не удалось. Например, y = x2. Это направляет мысль на собственно теоретический поиск, поиск необходимых и достаточных условий, обеспечивающих возможность подбора парной функции: y(0) = 0, Ef ? R, $ x0 ? 0: y(x0) = 0.

2.4.2. Расширение математического кругозора учащихся и риск утраты потребности к дедуктивному обоснованию математических утверждений

Средства экспериментальной математики в науке наиболее часто привлекаются к решению тех задач, попытки решения которых аналитическими методами долгое время оставались безуспешными (см. параграф 1.1 и параграф 1.2).

Подобное использование компьютерных средств особенно соблазнительно в педагогических ситуациях, когда учителям недостаточно учебного времени или уровня базовой математической подготовки учащихся для представления дедуктивного доказательства утверждения. Компьютерные динамические визуализации не только делают утверждения легко воспринимаемыми, но и убеждают учащихся в их истинности.

Пример 2. Теорема о сумме углов треугольника.

Учитель просит детей изобразить в GeoGebra произвольный треугольник, измерить его углы и создать на панели объектов функцию, вычисляющую их сумму (рис. 47). Он просит нескольких учащихся сообщить ему результат вычисления суммы углов треугольника. Затем просит всех убедиться в справедливости гипотезы, проведя эксперимент со свободным перемещением вершин построенного треугольника, изменением в каждой серии экспериментов настроек точности отображения данных. Для того чтобы развеять последние сомнения и скорректировать формулировку утверждения он просит найти и прочитать теорему в учебнике.

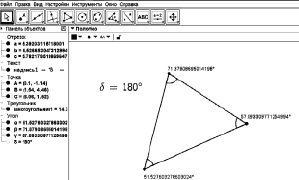
Рис. 47. Компьютерная визуализация теоремы о сумме углов треугольника

Психологические критерии убедительности, к которым учитель обращался в представленном сценарии, сродни тем, что использовались в древнем Египте и Индии: авторитетный источник и наглядность. Однако массовость полученных таким образом экспериментальных данных и степень их согласованности столь высока, что создается иллюзия превалирования этих критериев над дедуктивным доказательством. Ситуация усугубляется низким уровнем строгости представляемых в некоторых учебниках дедуктивных выводов данного утверждения, искусственностью предлагаемых дополнительных построений.

Несмотря на очевидность опасности частого обращения к таким сценариям для формирования потребности и навыков дедуктивных
доказательств, учителя часто злоупотребляют ими. Свои действия они объясняют тем, что введение математических утверждений посредством компьютерных визуализаций и контрольных экспериментов позволяет:

– экономить учебное время, высвобождая его для обучения решению задач;

– значительно расширить спектр известных учащимся опорных утверждений без существенной потери учебного времени;

– расширить математический кругозор учащихся за счет ознакомления с красивыми утверждениями, которые ранее могли быть включены в программу лишь для школ и классов с углубленным изучением математики.

Уменьшению обозначенных рисков, на наш взгляд, будут способствовать следующие профилактические мероприятия:

– демонстрация везде, где это возможно, неполной согласованности экспериментальных данных (подробнее об этом будет рассказано в параграфе 2.5);

– представление зависимости выводов от степени адекватности модели объекту исследования;

– расширение представлений учащихся о спектре функций дедуктивных рассуждений в математике: объяснение экспериментально установленных фактов, систематизация утверждений, логический контроль алгоритмов деятельности и т.п.

2.4.3. Помощь математическому видению учащихся и риск деградации визуального мышления

Системы динамической геометрии часто привлекаются к образовательному процессу не только для обеспечения возможности организации исследовательского обучения, но и в качестве средств создания динамической наглядности, которая позволяет компенсировать недостаток развития способности учащихся к математическому видению.

Так, например, разработчики программного продукта 1С: Математический конструктор включают в комплект электронных образовательных ресурсов не только саму среду, но и коллекцию готовых динамических листов, анимаций для постановки задач, а также наглядного представления аксиом и теорем. Подобные коллекции размещены и на официальных сайтах аналогичных программных продуктов [143, 151], а также в блогах учителей математики [139, 138], на сайтах профессиональных сообществ [142].

Динамическая наглядность в отличие от статической позволяет учащимся преодолеть сложившиеся стереотипы воображения, обнаружить множественность и многовариантность ситуаций, определяемых условием задачи, сделать видимой динамику реконструкции образов объекта исследования в ходе решения задачи.

Приведем конкретный пример, иллюстрирующий преимущества динамической наглядности над статической.

Пример 3. ABCD – параллелограмм, AB = 1, ВС = 2, а угол ABC – тупой. BE и DF перпендикулярны BС, BF и DE – стороне ВС. Найти площадь параллелограмма BFDE, подобного АВСD.

Стереотипным для учащихся является образ, представленный на рис. 48.

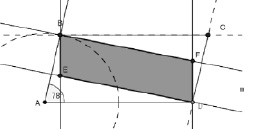
Рис. 48. Стереотипный образ задачной ситуации

Использование стереотипного чертежа приводит к уравнению:

,

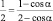где .

Результат решения этого уравнения противоречит условию «угол ABC – тупой». Обнаружить другую возможность образного представления задачной ситуации помогает динамический чертеж (рис. 49).

Однако увлечение учителей использованием готовой динамической наглядности, как показали проведенные нами исследования, негативно сказывается на развитии собственного визуального мышления учащих. Понятие визуального мышления было введено в научный оборот Р. Арнхеймом [107], под визуальным мышлением он понимает невербальное (не языковое) мышление, которое направлено на переработку информации, полученной от зрительных каналов восприятия. Несмотря на то, что математика имеет дело с абстракциями, высокий уровень развития визуального мышления имеет большое значения для математической
деятельности и успешного овладения математикой. Этот факт убедительно доказан исследованиями В.А. Далингера [37]. В своей монографии он показывает, что визуальное мышление выполняет в математической деятельности ряд важнейших операций: подбор зрительных образов для оказания помощи вербальному мышлению, создание чувственно не воспринимаемых образов или их частей под воздействием информации, хранящейся в памяти, упорядочивание, оценка и переоценка значимости образов, варьирование их структуры, перекодирование образов и др.

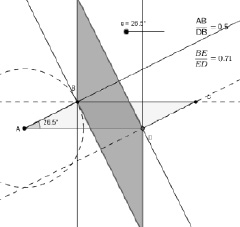
Рис. 49. Динамический чертеж для выделения ситуаций, соответствующих условию задачи

Снижению риска деградации визуального мышления, на наш взгляд, способствует уменьшение доли готовых динамических изображений в системе средств обучения математике. А именно, замещение их заданиями на самостоятельного создание динамических визуализаций и постановка задач, требующих внесения изменений в готовый динамический чертеж для решения задачи: изменения в наборе скрываемой части элементов, введение дополнительных построений, варьирование динамики изменений чертежа.

2.4.4. Формирование навыков компьютерного моделирования математических объектов и риск утраты навыков построения классическими конструктивными инструментами

Системы динамической геометрии обладают богатым набором инструментов для построения моделей геометрических объектов и геометрической интерпретации математических объектов иной природы. Они удобны и просты в использовании. Так, например, для построения графика функции достаточно записать ее уравнение в строке ввода. Для построения правильного многоугольника достаточно указать две его соседние вершины и общее количество вершин.

Однако набор инструментов среды не исчерпывает многообразие всех учебных объектов, поэтому наиболее часто визуализация объектов изучения требует построения собственных динамической моделей с использованием комплекса инструментов. Создание таких моделей в большинстве своем требует от учащихся знаний определений и признаков математических понятий.

Пример 4. Построить график производной функции y = f(x), представленной своим графиком.

Решение задачи начинается с построения точки D, принадлежащей графику производной функции и опирается на знания учащихся о том, что координатами такой точки являются: (x0; tg), где – угол наклона касательной к графику функции в точке А с абсциссой x0 (рис. 50).

Постановка подобных заданий очень полезна для освоения теоретических положений, поэтому изучение приемов построения динамических моделей целесообразнее всего осуществлять на уроках изучения нового материала или формирования навыков использования изученных фактов. Проведенные нами исследования показывают, что такая работа не требует больших затрат учебного времени. Однако обучение компьютерному моделированию не должно подменять обучение использованию классических конструктивных инструментов, так как в основе использования инструментов среды лежат принципы построения циркулем и линейкой. Полезно начинать осваивать инструменты среды с обучения построению циркулем и линейкой, затем освоенные приемы учиться реализовывать виртуальными инструментами. И лишь только после того, как сформированы прочные навыки использования приема, можно разрешить учащимся создать и применять виртуальный инструмент, представляющий собой результат решения базовой задачи на построение.

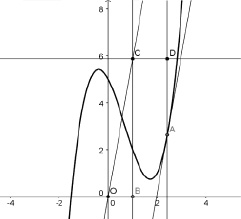
Рис. 50. Построение точки D, принадлежащей графику касательной заданной функции

Снижению риска утраты способности учащихся к построению классическими инструментами способствуют также задачи, где построения в среде носят лишь вспомогательный характер.

Пример 5. Построить окружность, которая проходит через точки А и В, и касается окружности с.

Компьютерное решение данной задачи оказывается весьма простым. Достаточно отметить на заданной окружности произвольную точку С, затем построить окружность, проходящую через три точки А, B и C соответствующим инструментом программы. Построенная окружность пересекает данную (в общем случае) в двух точках C и E. Для решения задачи нужно найти положение точки C на данной окружности с, при котором она совпадет с точкой E. Проблема состоит в использовании этого построения для обнаружения идеи построения циркулем и линейкой. На рис. 51 представлен компьютерный эксперимент, позволяющий обнаружить неподвижную точку F, которая будет использована для построения классическими ин-
струментами.

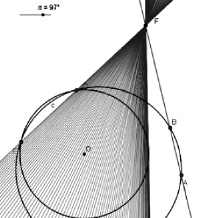
Рис. 51. Обнаружение неподвижной точки F в ходе компьютерного эксперимента

Подведем итог представленному обзору эффектов и рисков переноса в условия массового обучения методологии экспериментальной математики. Мы их намеренно представили попарно для того, чтобы обратить внимание на то, что вовсе не нужно отказываться от возможностей, предоставляемых новой методологией из-за опасения негативных последствий. Нужно лишь разумно ее применять, помня о том, что «лучшее враг хорошего».