Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

2.5. Эксперимент как средство предупреждения экспериментально-теоретического разрыва

2.5.1. Постановка задачи

Системы динамической математики, открыв дорогу исследовательскому подходу в обучении математике, принесли с собой ряд проблем, которые были кратко представлены в предыдущем параграфе. Здесь мы остановимся лишь на одной из них – проблеме риска возникновения экспериментально-теоретического разрыва. Его основное проявление, как было показано выше, состоит в том, что у школьников резко падает мотивация к проведению дедуктивных доказательств, что влечет за собой целый ряд негативных следствий: уменьшение способности к дедуктивным рассуждениям, падение интереса к теоретическому поиску, трудность или даже невозможность постановки новых задач путем логического преобразования решенной задачи и т.д.

Мы считаем, что феномен экспериментально-теоретического разрыва – это пятно на репутации педагогического сообщества, поскольку он происходит от недостаточно продуманного использования систем динамической математики. С этической точки зрения очевидно, что если один человек воздействует на другого, то он должен знать свойства инструментов воздействия, и при этом совершенно неважно, будет ли это физик со своим полигоном, хирург со своей операционной или преподаватель математики, использующий программный продукт образовательного назначения.

Очевидно, что не только он сам должен знать свойства этого программного обеспечения, но и позаботиться о том, чтобы его воспитанник, выступая в роли экспериментатора, знал свойства тех инструментов, которые он использует. Он должен знать и пределы измерений, и погрешность измерений, и участок линейности характеристики прибора, и многое другое. Кроме того, он должен понимать, что инструмент влияет на свойства изучаемого объекта, причем как на макроуровне, так и на микроуровне.

Настоящий параграф посвящен описанию результатов исследования свойств систем динамической математики, на примере GeoGebra, и демонстрации разнотипных эффектов их применения в изучении математики.

В данном параграфе мы сосредоточимся на важном свойстве GeoGebra, а именно, на приблизительности вычислений.

2.5.2. GeoGebra как ансамбль инструментов

Школьник «докомпьютерных» времен экспериментировал на стандартных листах бумаги с тремя инструментами: циркулем, линейкой и карандашом. При этом свойства инструментов были весьма немногочисленны и настолько просты, что не требовали для их изучения дополнительного времени. Прежде всего, очевидно, что размеры бумаги, длина линейки и величина циркуля не позволяли построить отрезок большой длины (например, длиной в 1 м) или провести окружность большого радиуса (например, радиусом 2 м). Кроме того, очевидно, что при измерении длин отрезков невозможно было надеяться на высокую точность, поскольку человеческий глаз не может дать разрешение менее 0,25 мм. Очевидно, наконец, что толщина линий зависела от свойств карандаша. Если карандаш представлял собой грифель в деревянной оболочке, то толщина линии обязательно была переменной в силу физических свойств рисования. Если же использовался автоматический карандаш, то толщина линии была постоянна и равна толщине грифеля, которая, согласно стандартам, равнялась либо 0,5 мм, либо 0,7 мм. Попытка отметить на отрезке какую-либо индивидуальную точку приводила к необходимости рисовать закрашенный кружочек, радиус которого был чуть больше, чем толщина линии.

Парадоксально, но с помощью несовершенных реальных инструментов приходилось формировать представления об идеальных геометрических объектах, например о бесконечно длинной прямой, состоящей из исчезающе малых точек. Еще более парадоксально, что эта задача разрешима, пусть и с некоторыми оговорками, о чем свидетельствует тысячелетний опыт преподавания математики.

При переходе к экспериментированию с помощью ИГС GeoGebra ситуация меняется довольно сильно. Прежде всего, резко возрастает количество инструментов, с помощью которых возможна организация экспериментов. Так, горизонтальное меню версии 4.4 содержит 12 иконок, за каждой из которых скрывается несколько конкретных инструментов. В результате общее количество инструментов, которыми может воспользоваться школьник, равняется 71-му, что в десятки раз превышает «докомпьютерные» возможности. Кроме того, появляется возможность строить «большие» объекты. Например, можно построить отрезок длиной 10 м с помощью инструмента «Отрезок с фиксированной длинной» и просмотреть его по частям с помощью инструмента «Переместить чертеж». Наконец, GeoGebra дает возможность производить вычисления с огромной точностью. Настройки по умолчанию предполагают, что длины отрезков выражаются в сантиметрах и могут быть найдены с точностью до 2-х десятичных разрядов. При этом предусмотрена возможность изменить количество разрядов и находить длины с точностью до 0, 1, 2, 3, 4, 5, 10 и 15 разрядов.

Для учителя очевидно, что GeoGebra представляет собой Ансамбль Инструментов (АИ), с помощью которых можно добиваться разнообразных педагогических целей. Однако даже если читатель не знаком ни с какими ИГС, содержание предыдущего абзаца означает, что главная характеристика описываемого продукта заключена в слове «среда». Для школьника, например, это действительно среда обитания, «населенная» многочисленными разнотипными инструментами, многие из которых имеют индивидуальные настройки. Для учителя очевидно, а хороший учащийся догадывается или чувствует, что многое нуждается в изучении: каждый отдельный инструмент, взаимодействие пар (или даже групп) инструментов, сопоставление показаний инструментов с известными математическими фактами… При этом заранее нельзя гарантировать, что такое изучение не выявит каких-либо обстоятельств, которые будут столь же неприятны, как кривизна пластмассовой линейки или толстая линия грифельного карандаша.

Последнее пессимистическое замечание вступает в определенное противоречие с опытом использования ИГС. Действительно, цель их создания состояла в том, чтобы ввести в процесс обучения геометрии возможность постановки математических экспериментов, с помощью которых школьники обучались бы формулировке гипотез о свойствах геометрических фигур и их последующей проверке. Эта цель была с блеском достигнута, о чем свидетельствуют результаты многочисленных исследований, проводимых учеными разных стран, например, В.И. Рыжиком [77], М.В. Шабановой [65], Th. Gawlick [116], C. Laborde [123], A. Mariotti [126] и многими другими. Тем не менее, в рамках данной главы мы сосредоточимся на выявлении странных, необычных, дисгармоничных, парадоксальных свойств АИ GeoGebra. Цель такого сосредоточения вполне позитивна, поскольку состоит в том, чтобы использовать парадоксальные показания инструментов для профилактики экспериментально-теоретического разрыва.

2.5.3. Внутренние и внешние конфликты ИГС

Искомые свойства ИГС могут быть выявлены пользователями в процессе выполнения ряда заданий. Они разбиваются на несколько групп, смысл которых будет выявлен по мере их возникновения.

Примем следующее терминологическое соглашение. Словосочетание «стандартная настройка» будет означать, что длины отрезков находятся с точностью до 2-х разрядов, а словосочетание «тонкая настройка» – до 15-ти разрядов.

Парадоксальные показания некоторых инструментов

Задание 1. Постройте произвольный отрезок AB (инструмент «Отрезок»). Отметьте на отрезке точку C (инструмент «Точка на объекте»). Найдите длины отрезков AC, CB и AB с помощью инструмента «Расстояние или длина» и прокомментируйте полученные результаты.

Обсуждение. Варьируя точки A, B или C с помощью инструмента «Перемещать», нетрудно получить результаты двух типов.

В первом случае мы получаем, что |AC| + |CB| = |AB| (см. рис. 52), а во втором – что |AC| + |CB| |AB| (см. рис. 53).

Парадокс: инструмент «Расстояние или длина» показывает, что существуют отрезки, для которых свойство аддитивности длины не выполняется.

Всюду в дальнейшем естественные, ожидаемые результаты эксперимента мы будем записывать в основном тексте, а парадоксальные, «неправильные» результаты будем фиксировать на отдельных рисунках в виде скрин-шотов.

Рис. 52

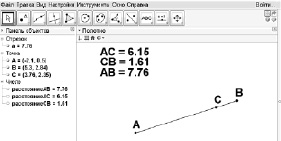
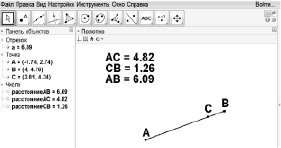
Рис. 53

Задание 2. Постройте лучи [OA) и [OB), а также луч [OС), лежащий внутри AOB (инструмент Луч). Найдите меры углов AOC, COB и AOB с помощью инструмента Угол и прокомментируйте полученные результаты.

Обсуждение. Варьируя точки A, B или C с помощью инструмента Перемещать, нетрудно получить либо ожидаемый результат типа

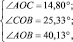
либо неожиданный результат, изображенный на рис. 54.

В первом случае мы получаем, что AOC + COB = AOB, а во втором – что AOC + COB AOB.

Парадокс: инструмент Угол показывает, что существуют углы, для которых свойство аддитивности меры угла не выполняется.

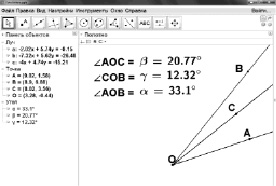
Рис. 54

Задание 3. Постройте DАВС (инструмент Многоугольник). На стороне ВС отметьте точку D (инструмент Точка на объекте). Постройте треугольники DАВD и DАСD (вновь инструмент Многоугольник). Найдите площади всех трех треугольников с помощью инструмента Площадь и прокомментируйте полученные результаты.

Обсуждение. Варьируя точки А, В, С или D с помощью инструмента Перемещать, нетрудно получить либо ожидаемый результат типа

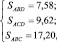
либо неожиданный результат, изображенный на рис. 55.

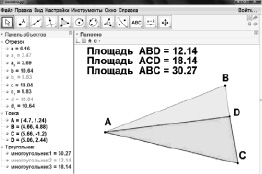
Рис. 55

В первом случае мы получаем, что SABD + SABD = SABC, а во втором – что SABD + SABD * SABC.

Парадокс: инструмент «Площадь» показывает, что существуют треугольники, для которых свойство аддитивности площади не выполняется.

Итак, эксперименты с инструментами Расстояние или длина, Угол и Площадь показывают, что, якобы, существуют объекты, для которых нарушаются фундаментальные свойства геометрических фигур. Для учителя важно, что эксперимент с ИГС на уроке не может быть пущен на самотек, иначе могут получиться результаты, противоречащие тем фактам, которые следует усвоить. Для ученика важно, что любые, самые простые эксперименты нуждаются в теоретическом осмыслении. Для обоих экспериментаторов, учителя и ученика, важно понять, что происходит при возникновении парадоксальных результатов: обнаружение неожиданных геометрических свойств, сбои в работе инструмента или что-то еще.

Вышеописанные парадоксальные результаты выявляют конфликты между АИ GeoGebra и математическими теоремами/аксиомами. Они являются внешними по отношению к GeoGebra. Рассмотрим теперь конфликты другого типа, а именно, конфликты между двумя инструментами, которые естественно трактовать как внутренние конфликты АИ GeoGebra.

Конфликты инструментов. Когда два субъекта противоборствуют в суде, используется юридический термин versus – против, сокращенно vs. Так, выражение Brown vs the United States означает дело «Браун против Соединенных Штатов» (пример заимствован их электронного словаря ABBYY Lingvo x5). В соответствии с этой традицией мы будем описывать конфликты инструментов.

Задание 4 (Расстояние или длина vs Отношение объектов). Найдите расстояние между точками A(0, 0) и B(0, 0.000000000000001) и определите, совпадают ли они.

Обсуждение. Выбрав инструмент Расстояние или длина и нажав на обозначения точек на панели объектов, мы найдем, что

|AB| = 0,000000000000001 = 10–15 см.

Это означает, что точки A и B не совпадают между собой. Если же выбрать инструмент Отношение объектов и применить его к точкам A и B, то получим такой ответ: «A и B идентичны (численное совпадение)» (рис. 56).

Парадокс: два разных инструмента АИ GeoGebra дают разные ответы на один и тот же вопрос.

Результаты выполнения задания 4 позволяют понять, что делает АИ GeoGebra, измеряет расстояния или вычисляет их. Дело в том, что расстояние 10–15 см примерно в 1000 раз меньше, чем размеры атомного ядра! В настоящее время не существует инструментов для непосредственного измерения таких расстояний, и в обозримом будущем такие инструменты не появятся. Следовательно, школьник может почти самостоятельно прийти к выводу, известному специалистам: при определении расстояний АИ GeoGebra вычисляет расстояния, исходя при этом из некоторых данных. Как только в рассуждениях появляется слово «вычисляет», сразу возникают вопросы о том, с какой точностью производятся вычисления, как изменятся результаты при изменении точности и т.п. В частности, мы будем заниматься влиянием точности вычислений на геометрическую трактовку результатов экспериментов.

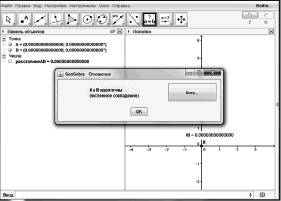
Рис. 56

Парадоксальные результаты работы инструмента Расстояние или длина (задание 1) позволяют предположить, что он может вступить в конфликт с инструментом Середина или центр. Для выяснения справедливости или несправедливости нашего предположения выполним следующее задание.

Задание 5 (Расстояние или длина vs Середина или центр). Постройте отрезок AB. С помощью инструмента Середина или центр найдите его середину C. С помощью инструмента Расстояние или длина определите длины отрезков AC, CB и AB и прокомментируйте полученные результаты.

Обсуждение. Варьируя точки A или B с помощью инструмента Перемещать, нетрудно получить либо ожидаемый результат типа

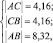
либо неожиданный результат, изображенный на рис. 57.

В первом случае мы получаем, что точка С равноудалена от концов отрезка, поэтому она действительно является его серединой. Во втором случае отрезок АВ «слишком короток» для того, чтобы точка, удаленная от его концов на 4,3 см, была его серединой.

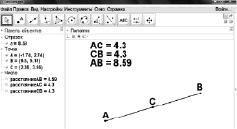
Рис. 57

Все предыдущие примеры использовали стандартную настройку округления. Если же применить тонкую настройку, то можно получить, что середина отрезка, определяемая с помощью инструмента «Середина или центр», не является равноудаленной от концов отрезка. Например, на рис. 58, полученном авторами, об этом говорят последние разряды в длинах отрезков АС и СВ.

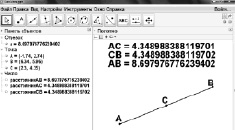
Рис. 58

Парадокс: точка, являющаяся серединой с точки зрения одного инструмента, может не быть серединой с точки зрения другого инструмента.

Парадоксальные результаты работы инструмента Угол (задание 2) позволяют предположить, что он может вступить в конфликт с инструментом Биссектриса. Для выяснения справедливости или несправедливости нашего предположения выполним следующее задание.

Задание 6 (Угол vs Биссектриса). Постройте лучи [OA) и [OB). С помощью инструмента Биссектриса проведите биссектрису угла АОВ и обозначьте её [OС). С помощью инструмента Угол найдите величины АОС, СОВ и АОВ и прокомментируйте полученные результаты.

Обсуждение. Варьируя точки А или В с помощью инструмента Перемещать, нетрудно получить либо ожидаемый результат типа

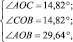
либо неожиданный результат, изображенный на рис. 59.

В первом случае мы получаем, что луч [OС) образует равные углы со сторонами АОВ и является его биссектрисой. Во втором случае раствор угла ОВ «слишком мал» для того, чтобы луч [OС) мог служить его биссектрисой.

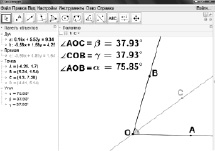
Рис. 59

При тонкой настройке округления нетрудно получить разные значения углов АОС и СОВ.

Парадокс: луч, являющийся биссектрисой с точки зрения одного инструмента, может не быть биссектрисой с точки зрения другого инструмента.

Задание 7 (Расстояние или длина vs Правильный многоугольник). Постройте равносторонний треугольник с помощью инструмента Правильный многоугольник. Найдите длины сторон с помощью инструмента Расстояние или длина. Прокомментируйте полученные результаты.

Обсуждение. При стандартной настройке округления получим ожидаемый результат: все стороны имеют одинаковую длину. Однако при тонкой настройке нетрудно получить странный результат, изображенный на рис. 60.

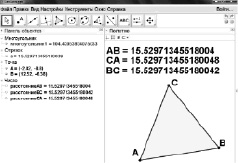
Рис. 60

Странность состоит в том, что длины сторон равностороннего треугольника, будучи измеренными, оказываются различными.

Парадокс: существуют треугольники, которые являются равносторонними с точки зрения одного инструмента и не являются таковыми с точки зрения другого инструмента.

Задание 8 (Расстояние или длина vs Окружность по центру и радиусу). С помощью инструмента Окружность по центру и радиусу постройте окружность с центром в точке A радиуса, например, 4. Постройте точку B на окружности (инструмент Точка на объекте). С помощью инструмента Расстояние или длина найдите расстояние |AB|. Двигая точку B по окружности (инструмент Перемещать), проследите, меняется ли расстояние |AB|. Прокомментируйте полученный результат.

Обсуждение. При стандартной настройке расстояние |AB| всегда постоянно и равно 4. Однако при тонкой настройке (и медленном движении точки) удается найти такие положения, при которых

|AC| = 4,000000000000001 или |AD| = 3,999999999999999

(рис. 61).

Парадокс: точка B, которая по построению обязана оставаться на окружности, может приближаться к центру или удаляться от него.

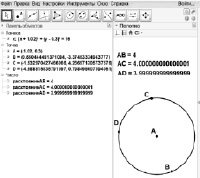
Рис. 61

Задание 9 (Расстояние или длина vs Отражение относительно точки). Постройте точки A и B. С помощью инструмента Отражение относительно точки отразите точку А относительно центра В, обозначив искомый образ через А. С помощью инструмента Расстояние или длина найдите расстояния |AB| и |AB|. Прокомментируйте полученный результат.

Обсуждение. При стандартной настройке всегда получаем ожидаемый результат |AB| = |AB|. Однако при тонкой настройке результаты могут оказаться неожиданными, например, такими, как на рис. 62.

Рис. 62

Парадокс: при центральной симметрии точка и ее образ могут находиться на разном расстоянии от центра.

Разумеется, список «конфликтующих» пар инструментов далеко не исчерпан, и мы предоставляет читателю возможность поискать другие пары, подобно тому, как мы делали это выше. Перейдем теперь к описанию противоречий между показаниями АИ GeoGebra и известными теоремами школьного курса математики.

«Опровержение» известных теорем. В учебно-методическом пособии Е.В. Потоскуева, посвященном геометрической подготовке учителя математики, содержится раздел «Рабочие теоремы планиметрии» [71, с. 369–376]. В нем собраны 50 теорем, которые, по мнению автора, наиболее часто используются при решении задач. Естественно, что первичное изучение всех их или многих из них могло бы использовать ИГС. Покажем, что эксперименты с АИ GeoGebra могут приводить к «опровержению» известных теорем. Разумеется, мы не будем проверять все 50 теорем, хотя это вполне возможно. Для примера выберем три из них, относящиеся к важным плоским фигурам – окружности, треугольнику и параллелограмму.

Задание 10. Постройте окружность по ее центру A и точке B на ней. Постройте точки C и D на окружности. Измерьте углы CAB и CDB с помощью инструмента Угол и прокомментируйте полученный результат.

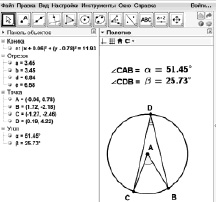
Рис. 63

Обсуждение. Варьируя точки B, C или D с помощью инструмента Перемещать, нетрудно получить результаты двух типов. Во-первых, может получиться ожидаемый результат, показывающий, что вписанный угол вдвое меньше центрального. Во-вторых, может получиться неожиданный результат, изображенный на рис. 63, который показывает, что не всякий центральный угол вдвое больше
вписанного.

Парадокс: отношение мер центрального и вписанного угла не является постоянным.

Задание 11. Постройте треугольник и проведите биссектрисы его углов. Каково взаимное расположение биссектрис?

Обсуждение. Очевидно, что биссектрисы пересекаются в одной точке, и это свойство сохраняется при любой вариации вершин треугольника. В попытке «разрушить» эту очевидность найдем точки D, E и F, являющиеся попарными пересечениями биссектрис. При стандартной настройке, а также при почти всех других настройках, одноименные координаты точек одинаковы, то есть D = E = F, а значит, биссектрисы действительно пересекаются в одной точке. Только при тонкой настройке мы можем получить парадоксальный результат, изображенный на рис. 64. Последние цифры в записи ординат точек D, E и F показывают, что эти точки попарно различны.

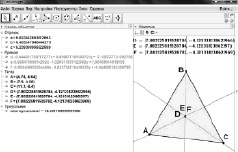
Рис. 64

Парадокс: существуют треугольники, у которых биссектрисы не пересекаются в одной точке.

Задание 12. Постройте параллелограмм, проведите его диагонали и найдите их середины. Прокомментируйте полученный результат.

Обсуждение. Если работать без панели объектов, то очевидно, что обе середины совпадают. Тем самым мы получаем красивый результат: точка пересечения диагоналей параллелограмма делит каждую из них пополам, откуда мгновенно получается, что параллелограмм является центрально-симметричной фигурой и что его противоположные стороны попарно равны. Для проверки чисто визуальных наблюдений
найдем середины диагоналей E и F и отобразим их на панели объектов. При стандартной настройке, а также при почти всех других настройках, одноименные координаты точек одинаковы, то есть E = F, а значит, первоначальное наблюдение оказывается верным. Только при тонкой настройке мы можем получить парадоксальный результат, изображенный на рис. 65, который показывает, что E F.

Парадокс: существуют параллелограммы, не имеющие центра симметрии.

Очевидно, что парадоксы, обнаруженные при выполнении заданий 10–12, выявляют конфликты, внешние по отношению к АИ GeoGebra.

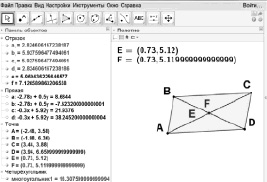
Рис. 65

Отступим от основной линии нашего изложения и отметим еще один конфликт, который относится не столько к математическому экспериментированию, сколько к отступлению от математических традиций.

Конфликт интерфейса и математических традиций. Хорошо известно, что задачи на построение циркулем и линейкой занимают достаточно важное место в курсе геометрии. Для этого существует несколько причин. Во-первых, такие задачи приобщают школьников к достаточно изощренной логике. Действительно, в процессе решения задачи учащемуся придется ответить на ряд вопросов.

1) Разрешима ли задача? Более точно, каковы дополнительные условия, необходимые и достаточные для разрешимости данной задачи?

2) Если задача разрешима, то сколько решений она имеет?

3) Каков алгоритм построения искомой геометрической фигуры?

Во-вторых, выявляется неочевидное для учащихся обстоятельство: сходство геометрической задачи на построение и алгебраической задачи по решению уравнения. Действительно, в процессе изучения уравнения A(x) = B(x) учащиеся обязательно отвечают на ряд вопросов, весьма сходных с вопросами предыдущего списка.

1. Каков критерий разрешимости уравнения данного типа?

2. Если уравнение разрешимо, то каков критерий единственности решения?

3. Если уравнение разрешимо, то по каким формулам можно получить список решений (конечное множество решений) или описание множества решений (бесконечное множество решений)?

По этой схеме изучаются линейные уравнения, уравнения вида ax + b = 0 (это не одно и то же), квадратные уравнения, тригонометрические уравнения, системы линейных уравнений и т.д. Интересно, что изучение дифференциальных уравнений, в частности, задачи Коши, следует той же логике, пусть и с некоторыми модификациями.

Таким образом, задачи на построение циркулем и линейкой, при всей своей специфике, приобщают школьников к математической культуре. Элементом этой культуры являются «запретительные» теоремы. Например, известно, что с помощью циркуля и линейки можно построить равносторонний треугольник, квадрат, правильный пятиугольник, правильный шестиугольник, однако нельзя построить правильный семиугольник. Именно наличие этого философского аспекта позволяет В.А. Успенскому утверждать, что «задачи на построение должны занимать достойное место в школьном курсе геометрии» [90, с. 108].

На этом фоне странным выглядит инструмент «Правильный многоугольник» АИ GeoGebra, который предлагает построить правильный многоугольник, указав одну его сторону и число вершин. В частности, этот инструмент предлагает построить правильный семиугольник! Неопытный пользователь, каковым является школьник, может приобрести иллюзию, что такое построение может быть реализовано с помощью циркуля и линейки. К счастью, от этой иллюзии можно избавиться, измерив длины сторон (см. задание 7). По-видимому, разработчикам интерфейса следовало назвать инструмент иначе, включив в название указание на приблизительность построения.

Вернемся к основной линии нашего изложения. Парадоксальные результаты, полученные в процессе выполнения заданий 1–12, хорошо иллюстрируют некий

ГЛОБАЛЬНЫЙ ПАРАДОКС: для каждого позитивного эксперимента, выполненного с целью получения формулировки той или иной теоремы школьного курса геометрии, существует негативный эксперимент, опровергающий справедливость этой формулировки.

На первый взгляд, наличие глобального парадокса бросает тень на ИГС. К счастью, это не так. Ниже мы покажем, что именно наличие этого парадокса может быть использовано для профилактики экспериментально-теоретического разрыва.

2.5.4. Эксперимент как профилактика
экспериментально-теоретического разрыва

В настоящее время ИГС легко доступны для каждой школы и каждого учителя. В этих условиях для учителя становится важным вопрос об отношении к ИГС, о выборе той ли иной стратегии их использования (или неиспользования). Перечислим некоторые из возможных стратегий.

1. Первая из возможных стратегий состоит в отказе от ИГС или в очень ограниченном их использовании, строго дозированном и обусловленном теми или иными конкретными причинами. Условно назовем такую стратегию консервативной.

При всей кажущейся неестественности консервативной стратегии она имеет под собой серьезные основания и, следовательно, право на существование. Прежде всего, следует помнить, что основной массив геометрических знаний сложился в те времена, когда компьютеры еще не были изобретены. В настоящее время этот массив продолжает интенсивно пополняться из разных источников, в частности, из тех, которые не имеют отношения к вычислительной технике. Кроме того, именно благодаря «безкомпьютерному» изучению математики все население приобщилось к достаточно изощренной логике, а также приобрело первоначальный опыт доказательных рассуждений и полноценной аргументации, которые так нужны в сложной социальной среде любому человеку независимо от его профессии. Наконец, следует помнить, что устойчивость сложных систем пропорциональна их полиморфизму. Например, современное супертехнологичное общество имеет с первобытным по крайней мере две общие черты: основным источником энергии является сжигание продуктов органического происхождения, а важным источником пищи – рыболовство, древнее апробированное занятие. Естественно предположить, что в будущем традиционный способ изучения математики будет иметь свою собственную нишу в систе-
ме образования.

2. Вторая из возможных стратегий состоит в том, чтобы во главу угла поставить позитивные компьютерные эксперименты, благодаря которым школьники будут обучаться формулировке гипотез о свойствах
геометрических фигур. При этом визуальная убедительность экспериментов считается достаточным обоснованием истинности гипотез, а дедуктивные обоснования предоставляются особо талантливым, любознательным, заинтересованным детям. Условно назовем такую стратегию инновационно-пассивной.

По мнению авторов, инновационно-пассивная стратегия не только неэффективна, но и просто вредна. Дело в том, что она полностью лишает учащихся культуры дедуктивных рассуждений. Трудно даже представить себе тот вред, который может нанести обществу массированное и/или длительное применение такой стратегии. К счастью, инновационно-пассивная стратегия не приобрела сколько-нибудь широкого распространения, хотя доводы в ее пользу не раз звучали в научных дискуссиях.

3. Третья стратегия также делает акцент на позитивные компьютерные эксперименты с последующим обязательным дедуктивным обоснованием выдвинутых гипотез. Условно назовем такую стратегию инновационно-активной.

По мнению авторов, именно инновационно-активная стратегия используется в настоящее время той частью педагогического сообщества, которая применяет в обучении компьютерные эксперименты. С этической и эмоциональной точки зрения такая стратегия выглядит весьма привлекательной. Повторимся: она приносит вполне ощутимые положительные результаты. К сожалению, практически неизбежным следствием такой стратегии является вышеупомянутый экспериментально-теоретический разрыв. Дело в том, что визуальная убедительность позитивных компьютерных экспериментов весьма высока, в силу чего исчезает мотивация для дедуктивных обоснований их результатов. Добавим к этому, что дедуктивные доказательства сами по себе могут оказаться достаточно сложными и трудоемкими, что еще больше снижает потребность в обосновании тех утверждений, которые и без того кажутся очевидными.

Прежде чем описывать четвертую стратегию, остановимся на одном из свойств чертежей античных математиков. По мнению авторов, чертежи античных математиков побуждали их создателей к дальнейшим исследованиям, и это стимулирующее воздействие было достаточно мощным. Действительно, чертежи выполнялись в лучшем случае на папирусе, то есть на не очень ровном шероховатом материале небольшого размера. Они выполнялись с помощью заточенного стебля тростника, вследствие чего линии имели достаточно большую толщину. В результате чертеж имел противоречащие друг другу свойства: с одной стороны, он помогал сформулировать гипотезу о свойствах изучаемых геометрических объектов, а с другой стороны, не давал никакой уверенности в том, что она соответствует действительности. В этих условиях дедуктивное доказательство было единственным способом установления истины.

4. Четвертая стратегия состоит в том, чтобы при изучении свойств геометрических фигур проводить оба эксперимента, и позитивный, и негативный. Позитивный эксперимент позволяет сформулировать гипотезу о свойствах геометрических фигур. В рамках школьной математики все такие гипотезы чрезвычайно красивы и привлекательны для учащегося-экспериментатора. Негативный эксперимент показывает, что выдвинутая гипотеза отнюдь не очевидна. Конфликт экспериментов не может быть разрешен в рамках экспериментального компонента математики. Для установления истины придется проводить дедуктивные рассуждения. Условно назовем такую стратегию исследовательской.

Отметим основную идею исследовательской стратегии: отрицательный компьютерный эксперимент призван играть ту же стимулирующую роль, какую играло несовершенство чертежей в античные времена.

По мнению авторов, содержательная (а отнюдь не административная) необходимость проводить дедуктивные рассуждения вызовет у учащихся интерес к ним, в результате чего будет освоен теоретический компонент математики. Предшествующие эксперименты будут способствовать освоению экспериментального компонента математики, а процесс самостоятельного выдвижения гипотез приобщит учащихся к исследовательской деятельности. В результате можно надеяться на повышение интереса к изучению математики и гармоничного ее освоения.

Отметим, что четвертая стратегия не обсуждалась ранее в научной литературе. При всей привлекательности ее теоретического обоснования, ее эффективность нуждается проверке посредством педагогического эксперимента.