Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

1.1. Кластерная модель структуры аморфного состояния полимеров

Предпосылкой для разработки кластерной модели структуры аморфного состояния полимеров послужили хорошо известные экспериментальные наблюдения. Как показали Ховард и его коллеги [1; 2], стеклообразные полимеры при деформировании их за пределом текучести (на плато холодного течения) подчиняются законам теории каучуковой высокоэластичности. Для описания поведения полимеров при больших деформациях в этом случае используются либо уравнение Ланжевена [3; 4], либо Гауссова трактовка [5], когда полимерная цепь не приближается к полностью вытянутому состоянию и соотношение между истинным напряжением     σ^ист    и степени вытяжки λ для одноосного растяжения имеет вид [5]:

σ^ист = G_p (λ² - λ^-1),                                        (1.1)

где G_p - так называемый модуль деформационного упрочнения.

Формально знание величины G_p позволяет определить плотность v_з сетки макромолекулярных зацеплений согласно хорошо известным формулам каучуковой эластичности [5]:

,                                                        (1.2)

и

,                                                         (1.3)

где М_з - молекулярная масса участка цепи между зацеплениями, ρ - плотность полимера, R - универсальная газовая постоянная, Т - температура испытаний, N_A - число Авогадро.

Однако попытки оценить величину М_з (или v_з) по определенным из уравнения (1.1) значениям G_p привели к неправдоподобно низким значениям М_з (или нереалистично высоким величинам v_з), противоречащим требованиям гауссовой статистики, которая предполагает наличие на участке цепи между зацеплениями не менее ~ 13 звеньев [6]. Возможные причины такого несоответствия при рассмотрении зацеплений как традиционных макромолекулярных «захлестов» достаточно подробно разобраны в работе [5]. В качестве принципиально отличающегося решения этой проблемы авторы [7-9] предположили, что кроме сетки указанных выше «захлестов» в стеклообразном состоянии полимеров имеется другой вид зацеплений, узлы которых по своему строению аналогичны кристаллитам  с вытянутыми цепями (КВЦ). Такой узел зацеплений имеет достаточно большую функциональность F (под функциональностью узла понимается число выходящих из него цепей [10]) и впоследствии он будет именоваться кластером. Схематическое изображение обоих указанных узлов зацеплений дано на рис. 1.1.

                                                                                                             
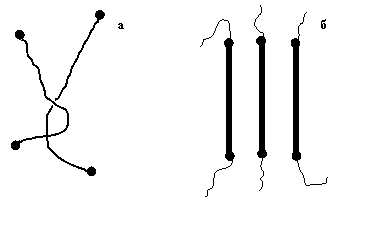
Кластер состоит из сегментов разных макромолекул и длина каждого такого сегмента постулируется равной длине статистического сегмента цепи l_ст («участка жесткости» цепи [11]). В таком случае эффективная (реальная) молекулярная масса участка цепи между кластерами             может быть рассчитана следующим образом [10]:

,                                                   (1.4)

где М_кл - молекулярная масса участка цепи между кластерами, рассчитанная по уравнению (1.2).

Очевидно, что при достаточно больших F можно получить разумные величины             , удовлетворяющие требованиям гауссовой статистики. В дальнейшем, чтобы различать параметры кластерной сетки зацеплений и сетки макромолекулярных «захлестов», мы будем использовать индексы «кл» и «з» соответственно. Таким образом, предложенная в [7-9] модель предполагает, что структура аморфного состояния полимеров представляет собой области, состоящие из коллинеарных плотноупакованных сегментов разных макромолекул (кластеры), погруженные в рыхлоупакованную матрицу, в которой концентрируется весь флуктуационный свободный объем полимера. Одновременно кластеры играют роль многофункциональных узлов сетки физических зацеплений. Величина F может быть оценена (вновь в рамках концепций каучуковой эластичности) следующим образом [12]:

,                                                  (1.5)

где G_∞ - равновесный модуль сдвига, k - постоянная Больцмана.

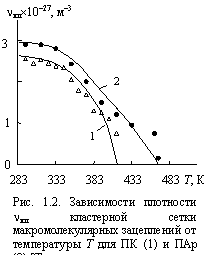
На рис. 1.2 приведены зависимости v_кл(Т) для поликарбоната на основе бисфенола А (ПК) и полиарилата (ПАр). Эти зависимости показывают уменьшение v_кл по мере роста Т, что предполагает термофлуктуационную природу кластеров (областей локального порядка). Кроме того, указанные зависимости обнаруживают две характеристические температуры. Первая из них, температура стеклования полимера Т_с, определяет полный распад кластеров, что соответствует переходу полимера в каучукоподобное состояние. Вторая, , соответствует перегибу на кривых v_кл(Т) и расположена примерно на 50 К ниже Т_с. 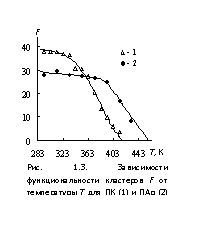Ранее, также в рамках концепций локального порядка, было показано [13; 14], что температура   ассоциируется с размораживанием сегментальной подвижности в рыхлоупакованных областях полимера. Это означает, что в рамках кластерной модели    можно ассоциировать с расстекловывание рыхлоупакованной матрицы. Аналогичный вид имеют и зависимости F(T) для этих же полимеров (рис. 1.3).

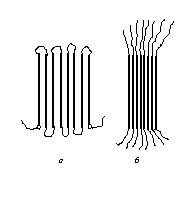
Две основные модели областей локального порядка в полимерах (со сложенными и вытянутыми цепями, см. рис. 1.4) имеют общую точку соприкосновения: они играют роль узлов физической сетки макромолекулярных зацеплений [7; 15]. Однако их реакция на механическое деформирование должна существенно различаться: если при больших деформациях области со сложенными цепями («пачки») способны к разворачиванию складок в распрямленные конформации, то кластеры такой возможности не имеют и деформирование полимера может происходить только путем распрямления «проходных» (соединяющих кластеры) цепей, т.е., ориентацией их в направлении проложенного напряжения. Возвращаясь к аналогии с кристаллической морфологией полимеров, отметим, что большие деформации аморфно-кристал-лических полимеров (особенно для полиэтиленов, составляющие 1000 ¸ 2000 %) реализуются за счет разворачивания складок кристаллитов [16]. Поэтому, используя величины предельных деформаций полимеров, можно получить доводы в пользу того или иного типа областей локального порядка в аморфном состоянии полимеров, что было сделано в работе [17].

  

Рис. 1.4. Два основных типа областей локального порядка в аморфном состоянии полимеров: со сложенными (а) и вытянутыми (б) (кластер) цепями [9].

Авторы [15] предположили, что «пачки» способны поставлять участки цепей в «междуузлия» (т.е., в межпачечные области) путем разворачивания складок, действуя в этом смысле аналогично кристаллитам со сложенными целями (КСЦ). В свете этого рассуждения обращает на себя внимание большое различие предельных степеней вытяжки λ_пр аморфно-кристаллических полимеров как полиэтилен высокой плотности (ПЭВП) и полипропилен (ПП), для которых развертывание складок кристаллитов при больших деформациях доказано экспериментально (λ_пр ≈ 1,6 для ПК; ≈ 6 для ПП и ≈ 13 для ПЭВП при комнатной температуре [16]). Это различие делает необходимыми количественные оценки для его объяснения [17].

Джент и Мэден [18] предположили, что вытяжка происходит в результате распрямления кристаллических и аморфных последовательностей цепей и в этом случае величину λ_пр можно выразить через число раз f, которое молекула проходит через один и тот же кристаллит (или «пачку»):

,                                      (1.6)

где K - степень кристалличности, n_ст - число эквивалентных статистических звеньев между узлами зацеплений в расплаве полимера. Обычно n_ст варьируется от 100 до 300; поскольку эта величина существенно не влияет на результаты оценок, то для всех использованных в работе [17] полимеров она была принята равной 225.

                                                                                                               Таблица 1.1

Оценка параметра складывания f для аморфных и аморфно-кристаллических полимеров [17]

Понятно, что величина f определяет число складок, которые макромолекула образует в КСЦ (или «пачке»).   Для образования складок необходимо выполнение условия f ≥ 2. Оценки f для ПЭВП и ПП, приведенные в табл. 1.1, дали ожидаемый результат: макромолекула первого из них складывается более 50 раз, а второго - ~ 5 раз, что хорошо согласуется с известными данными [18].

Эквивалентом степени кристалличности К для аморфных стеклообразных полимеров является относительная доля кластеров φ_кл. Оценку величины φ_кл можно выполнить следующим образом. Общая длина макромолекул L на единицу объема полимера в предположении их плотной упаковки равна [19]:

                                                                                                                         L = S^-1,                                                                 (1.7)

где S - площадь поперечного сечения макромолекулы.

Длина статистического сегмента l_ст оценивается так [20]:

                                                                                                                          l_ст = l₀C_∞,                                                             (1.8)

где l₀ - длина скелетной связи основной цепи, С_∞ - характеристическое отношение, которое является показателем статистической гибкости макромолекулы [21].

Общая длина сегментов, входящих в кластеры, L_кл на единицу объема полимера оценивается следующим образом [22]:

                                                                                                                           L_кл = l_стv_кл,               .                                           (1.9)

а величина φ_кл как отношение [9]:

               .                                       (1.10)

Сочетание уравнений (1.7) ÷ (1.10) позволяет получить окончательную формулу для расчета величины φ_кл [9]:

                                                                                                                            φ_кл = Sl₀C_∞v_кл.                                                    (1.11)

Полученные согласно уравнению (1.11) значения φ_кл приведены в табл. 1.1 для ПК и ПАр. Как показали расчеты для указанных полимеров с использованием экспериментальных значений λ_пр, во всех случаях f < 1 [табл. 1.1]. Это означает отсутствие складывания макромолекул этих полимеров в областях локального порядка (узлах физической сетки макромолекулярных зацеплений). Отметим также, что в аморфно-кристаллических полимерах развертывание складок в кристаллитах начинается при деформациях порядка 50 ÷ 100 % [23]. Если использовать в уравнении (1.6) величину λ_пр для аморфных областей ПЭВП ~ 2,0 и φ_кл ≈ 0,20, то получим f < 1, а это означает, что складывание макромолекул в аморфно-кристаллических полимерах реализуется только в кристаллических областях [9].

Таким образом, выполненные в работе [15] расчеты показали, что наиболее вероятным типом надсегментальных структур в аморфном состоянии полимеров является аналог кристаллита с вытянутыми цепями - кластер [рис. 1.1б].

И в заключение раздела укажем, что величина φ_кл является параметром порядка структуры аморфного состояния полимеров в строгом физическом смысле этого термина [24; 25].