Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

3.1. Турнир по экспериментальной математике

Одной из форм работы по реализации модели исследовательского обучения в стиле экспериментальной математики во внеурочной деятельности является турнир по экспериментальной математике. Его основная задача – привлечение внимания учащихся к экспериментальным методам, демонстрация их роли в решении математических задач, а также оценка уровня сформированности умений учащихся применять эти методы при решении математических задач.

Задания турнира составляются таким образом, чтобы не только представить учащимся экспериментальные методы, но и вовлечь учащихся в различные виды деятельности, связанные с их использованием:

– разрешение парадокса, порожденного несогласованностью выводов, основанных на теоретических фактах и экспериментальных данных;

– планирование решения поставленной математической задачи указанным экспериментальным методом;

– решение математической задачи указанным экспериментальным методом;

– решение серии взаимосвязанных задач («снежного кома» задач) на построение ограниченным набором инструментов компьютерной среды;

– привлечение компьютерного эксперимента к решению исследовательской задачи в качестве вспомогательного метода;

– постановка новых исследовательских задач на основе экспериментирования с компьютерной моделью объекта исследования.

Данный турнир был впервые проведен в 2015 году [148]. Приведем примеры задач этого турнира с решениями и критериями оценки.

3.1.1. Задачи турнира для учащихся 7 класса

Задание 1 (max 8 баллов). Вырежьте из листа бумаги квадрат. Измерьте его сторону и вычислите площадь. Затем разрежьте его так, как показано на рисунке (рис. 66). Составьте из полученных частей прямоугольник, измерьте его стороны и вычислите площадь. Сравните полученные значения площадей прямоугольника и квадрата, объясните результат.

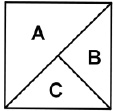
Рис. 66. Квадрат для задания 1

Критерии оценивания

Решение задания 1. Известно, что равносоставленные планиметрические фигуры равновелики. Однако на практике можно говорить лишь о приближенном равенстве равносоставленных фигур. Это и подтвердил проведенный нами эксперимент, в котором требовалось измерить стороны данного квадрата, найти произведение приближенных значений длин для вычисления его площади, разрезать квадрат и составить из него новую фигуру, похожую на прямоугольник, применить для вычисления ее площади формулу прямоугольника, измерением найти его стороны.

Все выделенные действия являются неустранимыми причинами появления (нарастания) погрешностей: погрешность измерения, погрешность выбора метода вычисления, погрешность вычисления. Ими объясняется полученное в ходе эксперимента неравенство площадей.

Задание 2 (max 10 баллов). Отрезок АВ (тонкая легкая однородная трубка) разделен точкой С на два отрезка в отношении m : n, где m и n целые числа. Опишите эксперимент, позволяющей методом взвешивания найти значения m и n. Перечислите оборудование, которое Вам для его проведения понадобится.

Критерии оценивания

Решение задания 2 (один из возможных вариантов).

Оборудование:

1) набор гирь одинаковой массы;

2) штатив для закрепления нити;

3) нить для подвеса трубки и гирь;

4) инструмент для того, чтобы проделать отверстия на концах трубки и в точке С.

Ход эксперимента: подвесить трубку, закрепив нить в точке С. Добиться равновесия, подвешивая гири в точках А и В. Подсчитать количество одинаковых гирь, подвешенных в точках А и В. Пусть, после подсчета оказалось, что в точке А подвешено k1 гирь, а в точке В – k2 гирь. Считая, что точка С является центром масс системы двух материальных точек (А; k1 (ед. массы)) и (B; k2 (ед. массы)). Опираясь на правило рычага (рис. 67), приходим к выводу:

АС : СВ = k2 : k1.

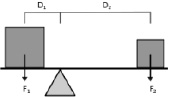
F1D1 = F2D2

Рис. 67. Иллюстрация правила рычага

Задание 3 (max 15 баллов). Возьмите лист бумаги с неровными краями. Проведите на нем произвольно прямую, отметьте две точки О и А. Пусть О – центр воображаемой окружности, точка А – точка, лежащая на этой окружности. Опишите, как перегибанием листа бумаги узнать, пересекает ли прямая воображаемую окружность. Пользуясь этим методом найдите точки пересечения построенной прямой и воображаемой окружности с центром О и радиусом ОА, или покажите, что их нет.

Критерии оценивания

Решение задания 3. Сложить лист бумаги, проведя одну линию сгиба по прямой l, а другую через точки О и А. Удерживая точку О, постараться согнуть лист так, чтобы точка А попала на прямую l. Отметить на l все возможные места расположения точки А (рис. 68).

Если уложить не удалось, то точек пересечения окружности и прямой нет.

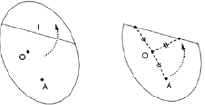
Рис. 68. Иллюстрация решения задачи 3

Если удалось отметить только одно место расположения точки А, то прямая l касается окружности с радиусом ОА.

Если удалось отметить два места, то окружность и прямая пересекаются в этих точках.

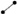Задание 4 (max 20 баллов). Панель инструментов GeoGebra состоит только из пяти инструментов: Точка , Отрезок по двум точкам , Луч по двум точкам 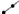, Окружность по центру и точке и Пересечение двух объектов 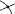. Решите следующую последовательность задач на построение в GeoGebra:

1) Построить правильный треугольник данными инструментами. Использовать результат решения задачи, чтобы дополнить панель инструментов своим инструментом Правильный треугольник. Сохранить файл под своей фамилией, например, Ivanov_4.1.ggb.

2) Убрать с панели инструмент Окружность по центру и точке . С помощью оставшихся инструментов построить произвольный отрезок и разделить его пополам. Использовать результат решения задачи, чтобы дополнить панель инструментов своим инструментом Середина отрезка. Сохранить файл под своей фамилией, например, Ivanov_4.2.ggb.

3) Убрать с панели инструментов инструмент Правильный треугольник. Добавить инструмент Окружность по центру и точке. Построить произвольную прямую и точку, не лежащую на ней. Провести через эту точку прямую, параллельную данной. Использовать результат решения задачи, чтобы дополнить панель инструментов своим инструментом Параллельная прямая. Сохранить файл под своей фамилией, например, Ivanov_4.3.ggb.

4) С помощью набора инструментов, полученных в результате решения задачи 3, построить произвольный угол и точку, лежащую вне его. Построить угол равный данному, с вершиной в этой точке. Сохранить файл под своей фамилией, например, Ivanov_4.4.ggb.

5) С помощью набора инструментов, полученных в результате решения задачи 3, построить произвольный угол и провести его биссектрису. Сохранить файл под своей фамилией, например, Ivanov_4.5.ggb.

Критерии оценивания

Решение задания 4

1. Построить правильный треугольник данными инструментами. Использовать результат решения задачи для того, чтобы дополнить панель инструментов своим инструментом Правильный треугольник.

Чтобы построить правильный треугольник, необходимо выполнить следующие шаги:

а) Построить окружность с центром в точке А и радиусом АВ.

б) Построить окружность с центром в точке В и радиусом АВ.

с) Найти точку пересечения этих окружностей.

д) Соединить эту точку с концами отрезка АВ (см. рис. 69).

Затем создать инструмент согласно выданной на Турнире инструкции.

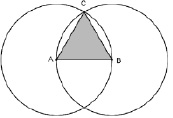
Рис. 69. Построение правильного треугольника

2. Убрать с панели инструментов инструмент Окружность по центру и точке. С помощью оставшихся инструментов построить произвольный отрезок и разделить его пополам. Использовать результат решения задачи, чтобы дополнить панель инструментов своим инструментом Середина отрезка.

Чтобы построить середину отрезка, необходимо выполнить следующие шаги:

а) Построить два правильных треугольника на одной стороне АВ.

б) Соединить противоположные вершины этих треугольников (см. рис. 70).

Затем создать инструмент согласно выданной на Турнире инструкции.

3. Убрать с панели инструментов инструмент Правильный треугольник. Добавить инструмент Окружность по центру и точке. С помощью оставшихся инструментов построить произвольную прямую и точку, не лежащую на ней. Провести через эту точку прямую, параллельную данной. Использовать результат решения задачи, чтобы дополнить панель инструментов своим инструментом Параллельная прямая.

Чтобы построить прямую, параллельную данной через точку, не лежащую на этой прямой, необходимо выполнить следующие шаги:

а) Построить окружность с центром в точке А и радиусом АВ.

б) Найти точку пересечения окружности с прямой (точка С).

в) Построить окружность с центром в точке С и радиусом СВ.

г) Найти точку пересечения этих окружностей (точка D).

д) Провести луч DС.

е) Найти точку пересечения луча с окружностью с центром в точке С (точка F).

ж) Построить луч FВ.

з) Построить луч ВF (см. рис. 71).

Затем создать инструмент согласно выданной на Турнире инструкции.

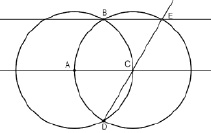
Рис. 71. Построение параллельной прямой

4. С помощью набора инструментов, полученных в результате решения задачи 3, построить произвольный угол и точку, лежащую вне его. Построить угол равный данному, с вершиной в этой точке.

Чтобы построить угол, равный данному (угол ВАС) с вершиной в точке (точка D), лежащей вне его, с помощью инструмента Параллельная прямая, необходимо:

1) провести через эту точку прямые, параллельные сторонам угла, а затем

2) отложить на них лучи DE и DF (см. рис. 72). Угол EDF равен углу ВАС по теореме о соответственных углах.

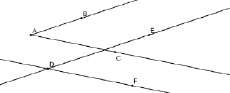
Рис. 72. Построение угла, равного данному

5. С помощью набора инструментов, полученных в результате решения задачи 2, построить произвольный угол и провести его биссектрису.

Чтобы построить биссектрису угла с помощью инструмента Середина отрезка, необходимо выполнить следующие шаги:

а) Построить угол САВ.

б) Построить окружность с центром в точке А и радиусом АС.

в) Отметить точки пересечения окружности со сторонами угла (точки С и D).

г) Найти середину отрезка CD (точка E).

д) Провести луч АE – искомую биссектрису угла САВ (см. рис. 73).

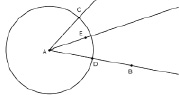
Рис. 73. Построение биссектрисы угла

Задание 5 (max 30 баллов). Даны две точки А и В. Экспериментально установите вид фигуры, образованной основаниями перпендикуляров, которые опущены из точки А на всевозможные прямые, проходящие через точку В. Обоснуйте правильность выводов, сделанных на основе эксперимента.

Критерии оценивания

Решение задания 5

Эксперимент: Пусть СВ – одна из прямых, проходящих через точку В. Опустим на нее перпендикуляр из точки А с основанием Н. Введем функцию для точки Н «оставлять след» и будем перемещать точку С.

Гипотеза: Основания перпендикуляров описывают окружность с диаметром АВ (см. рис. 74).

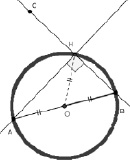
Рис. 74. Иллюстрация выдвинутой гипотезы

Доказательство:

1. Пусть Н лежит на окружности с диаметром АВ, тогда треугольники АОН и ВОН – равнобедренные. Следовательно, в этих треугольниках
равны углы при основаниях. Пусть угол при вершине А равен , а при вершине В – . Тогда угол при вершине Н равен ( + ). Применим к треугольнику AHВ теорему о сумме углов треугольника, тогда получаем: + = 90о, т.е. Н – основание перпендикуляра, опущенного из точки А на некоторую прямую, проходящую через точку В.

2. Пусть Н – основание перпендикуляра, опущенного из точки А на прямую ВС, проходящую через точку В. Докажем методом от противного, что Н лежит на окружности с диаметром АВ. Для этого допустим, что Н не лежит на окружности с диаметром АВ. Если прямая ВС пересекает окружность в некоторой точке Н1, то согласно доказанному в пункте 1, АН1 перпендикулярна ВС. Если точки Н и Н1 различны, то из одной точки проведено два различных перпендикуляра к одной прямой, что противоречит известной теореме. Следовательно, Н и Н1 совпадают, т.е. Н лежит на окружности с диаметром АВ. Если ВС не имеет других общих точек с окружностью диаметра АВ, то В является основанием перпендикуляра, проведенного к ВС из точки А. Н и В в этом случае также совпадают. Таким образом доказано, что Н лежит на окружности с диаметром АВ при любом расположении прямой ВС.

Задание 6 (по 10 баллов за каждую корректно поставленную задачу). Изменяя чертеж к заданию 5, составьте как можно больше новых задач. Формулировки своих задач можно записать или на листе бумаги, или в графическом окне GeoGebra с помощью инструмента Надпись .

Параметры изменения чертежа и примеры задач, которые могли бы быть составлены:

А. Изменение положения точки, описывающей фигуру.

5.1. Пусть Н – основание перпендикуляра из задания 5. Установите вид фигуры, образованной серединами отрезков АН и ВН.

5.2. Пусть Н – основание перпендикуляра из задания 5. Установите вид фигуры, образованной точками Е и F, лежащими на АН и ВН соответственно, где HE = k*HB, а AF = k*HA.

В. Изменение характеристического свойства описываемой фигуры:

5.3. Даны две точки А и В. Какую фигуру образовывает множество точек H таких, что АHВ = .

5.4. Даны две точки А и В. Какую фигуру образовывает множество точек Х таких, что HАВ = k*HВА.

С. Изменение данных объектов:

5.5. Дана точка А и окружность w. Постройте фигуру, образованную основаниями перпендикуляров, опущенных из точки А на всевозможные касательные к данной окружности. Как зависит вид фигуры от взаимного расположения точки и окружности.

3.1.2. Задачи турнира для учащихся 8 класса

Задание 1 (max 8 баллов). Вырежьте из бумаги квадрат со стороной 8 см. Разрежьте его так, как показано на рис. 75, а. Сложите из его частей прямоугольник так, как показано на рис. 75, б. Сравните площади квадрата и прямоугольника. Объясните результат.

а б

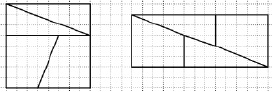
Рис. 75

Критерии оценивания

Решение задания 1. Известно, что равносоставленные планиметрические фигуры равновелики. Однако на практике можно говорить лишь о приближенном равенстве равносоставленных фигур. Это и подтвердил проведенный нами эксперимент, в котором требовалось вырезать квадрат, разрезать его и составить из него новую фигуру, похожую на прямоугольник, применить для вычисления ее площади формулу прямоугольника, измерением найти его стороны.

Все выделенные действия являются неустранимыми причинами появления (нарастания) погрешностей: погрешность измерения, погрешность выбора метода вычисления, погрешность вычисления. Ими объясняется полученное в ходе эксперимента неравенство площадей.

Задание 2 (max 10 баллов). В равностороннем треугольнике АВС (тонкой треугольной однородной пластине) провели медиану АМ. На ней отметили точку О, так что АО : OM = m : n, где m и n – целые числа. Опишите эксперимент, позволяющий методом взвешивания найти значения m и n. Перечислите оборудование, которое Вам для его проведения понадобится.

Критерии оценивания

Решение задания 2 (Один из возможных вариантов)

Оборудование:

1) набор гирь одинаковой массы;

2) штатив для закрепления нити;

3) нить для подвеса пластины и гирь;

4) инструмент для того, чтобы проделать отверстия в пластине.

Ход эксперимента: Подвесить пластину на нити, прикрепленной в точке О. В вершинах пластины подвешивать гири до тех пор, пока пластина не примет горизонтальное положение. Подсчитать количество гирь подвешенных в каждой из вершин. Пусть, после подсчета оказалось, что в точке А подвешено k1 гирь, а в точках В и С – k2 гирь. В этом случае точка О может рассматриваться как центр масс системы трех материальных точек (А; k1 (ед. массы)), (B; k2 (ед. массы)) и (С; k2 (ед. массы)). Так как М середина ВС, то эту систему можно заменить системой двух точек: (А; k1 (ед. массы)) и (М; 2k2 (ед. массы)) с центром масс в точке О. Применяя правило рычага (см. рис. 67) для этой системы, приходим к выводу: АО : ОМ = 2k2 : k1.

Задание 3 (max 15 баллов). Возьмите лист бумаги с неровными краями. На нем произвольно отметьте три точки А, В и С. Перегибанием листа бумаги найдите центр окружности, проходящей через эти три точки. Обоснуйте правильность построений.

Критерии оценивания

Решение задания 3

Построение: Нужно перегнуть лист бумаги два раза. Первый раз перегнуть так, чтобы совместились точки А и В, второй – чтобы совместились точки В и С. Точка пересечения линий сгибов – центр окружности, проходящей через точки А, В и С (см. рис. 76).

Обоснование: О – точка равноудаленная от каждой пары точек А и В; В и С по определению окружности. Множество точек плоскости, равноудаленных от двух данных, есть серединный перпендикуляр к отрезку. Линии сгиба являются серединными перпендикулярами к отрезкам АВ и ВС, поэтому точка О определяется как точка их пересечения.

Задание 4 (max 20 баллов). См. задачу 4 для учащихся 7 класса.

Задание 5 (max 30 баллов) (Задача предложена В.И. Рыжиком). В квадрат АВСD вписан треугольник АМN (точки М и N лежат на сторонах квадрата). В треугольнике AMN из вершины А проведена высота АH. Известно, что угол NAM равен 45°. Какую кривую опишет точка Н, если перемещать точку N по периметру квадрата?

Решение задачи 5

Эксперимент. Для точки Н зададим функцию «оставлять след» и будем перемещать точку N по периметру квадрата. Пусть точка N лежит
на стороне, противолежащей вершине А. Точка Н опишет дугу DВ (рис. 77). Если же точка N лежит на стороне с концом А, то точка H опишет дугу DAB.

Гипотеза. Основание перпендикуляра описывает фигуру, состоящую из двух дуг: дуги окружности с центром в точке А радиусом АD и дуги с центром О (центр квадрата) и радиусом ОА.

Случай 1. Точка N лежит на стороне, противолежащей вершине А.

Докажем, что основание перпендикуляра лежит на дуге BD окружности с центром в точке А. Пусть точка N лежит на стороне, противолежащей вершине А (например, ВС). На прямой ВС отложим отрезок ВЕ = MD, как показано на рис. 78. Прямоугольные треугольники АВЕ и ADM равны по двум катетам. Откуда следует, что АЕ = АM. Легко доказать, что треугольники АЕN и AMN равны по двум сторонам и углу между ними. Так как в равных треугольниках соответственные элементы равны, то высоты АВ и АН тоже равны. Таким образом, высота АН равна стороне квадрата, следовательно, лежит на дуге BD окружности с центром в точке А.

Докажем, что точка Н, лежащая на дуге, является основанием высоты, описываемого в задаче треугольника с углом 45°. Пусть точка Н лежит на дуге BD окружности с центром в точке А (см. рис. 79). Построим треугольник, в котором АН является высотой, а вершины N и M лежат на сторонах ВС и CD. Треугольники ABN и AHN равны по гипотенузе и катету. Аналогично равны треугольники AHM и ADM. Из равенства треугольников следует равенство соответствующих углов. Рассмотрим углы при вершине А. В сумме они составляют 90°, следовательно, сумма углов NAH и MAH равна половине, то есть 45°.

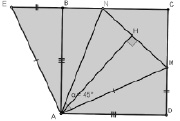
Рис. 78

Случай 2. Точка N лежит на стороне с концом в точке А.

Докажем, что основание перпендикуляра лежит на дуге BАD окружности с центром в точке О. Пусть точка N лежит на стороне, содержащей вершину А (например, ВА). Точка N в данном случае совпадает с вершиной С. Построим высоту АЕ треугольника AMN. Получившийся треугольник АМЕ – прямоугольный, его вершина лежит на окружности с диаметром АМ = АС и центром О (см. рис. 80).

Докажем, что точка Е, лежащая на дуге BAD, является основанием высоты, описываемого в задаче треугольника с углом в 45°. Пусть точка Е лежит на дуге BАD окружности с центром в точке О. Соединим точку Е с точками М и А. ЕМ пересекает АВ в точке N. Треугольник АМN является треугольником с углом в 45°, а АЕ – его высота.

Задание 6 (по 10 баллов за каждую корректно поставленную задачу). Изменяя чертеж к задаче 5, составьте как можно больше новых задач. Формулировки своих задач можно записать или на листе бумаги, или в графическом окне GeoGebra с помощью инструмента – Надпись.

Некоторые из задач, которые могли бы быть составлены:

5.1. Изменится ли и, если изменится, то как ответ в задаче 5, если угол NAM равен 30°- 60°

5.2. В квадрат АВСD вписан треугольник АМN (точки М и N лежат на сторонах квадрата). В треугольнике AMN из вершины А проведена медиана АH. Известно, что угол NAM равен 45°. Какую кривую опишет точка Н, если перемещать точку N по периметру квадрата?

3.1.3. Задачи турнира для учащихся 9 класса

Задание 1 (max 8 баллов). Вырежьте из бумаги прямоугольник со сторонами 8 и 13 см. Затем разрежьте его так, как показано на рис. 81.
Сложите из его частей прямоугольник так, как показано на рис. 82. Сравните их площади. Объясните результат.

Рис. 81 Рис. 82

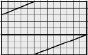
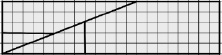
Критерии оценивания

Решение задания 1. Известно, что равносоставленные планиметрические фигуры равновелики. Однако на практике можно говорить лишь о приближенном равенстве равносоставленных фигур. Это и подтвердил проведенный нами эксперимент, в котором требовалось вырезать квадрат, разрезать его и составить из него новую фигуру, похожую на прямоугольник, применить для вычисления ее площади формулу прямоугольника, измерением найти его стороны.

Все выделенные действия являются неустранимыми причинами появления (нарастания) погрешностей: погрешность измерения, погрешность выбора метода вычисления, погрешность вычисления. Ими объясняется полученное в ходе эксперимента неравенство
площадей.

Задание 2 (max 10 баллов). На стороне АВ произвольного треугольника АВС (тонкой однородной треугольной пластине) отметили точку К, так что АК : КВ = m : n, где m и n – целые числа. На отрезке СК отметили точку О, так что СО : OК = p : k, где p и k – целые числа. Опишите
эксперимент, позволяющей методом взвешивания определить, в каком отношении точки К и О делят отрезки АВ и СК соответственно. Перечислите оборудование, которое Вам для его проведения понадобится.

Критерии оценивания

Решение задания 2 (Один из возможных вариантов).

Оборудование:

1) набор гирь одинаковой массы;

2) штатив для закрепления нити;

3) нить для подвеса пластины и гирь;

4) инструмент для того, чтобы проделать отверстия в пластине.

Ход эксперимента: Подвесить пластину на нити, прикрепленной в точке О. В вершинах пластины подвешивать гири до тех пор, пока пластина не примет горизонтальное положение. Подсчитать количество гирь, подвешенных в каждой из вершин. Пусть, после подсчета оказалось, что в точке А подвешено k1 гирь, в точке В – k2 гирь, а в точке С – k3 гирь.

В этом случае точка О может рассматриваться как центр масс системы трех материальных точек (А; k1 (ед. массы)), (B; k2 (ед. массы)) и (С; k3 (ед. массы)), а точка К как центр масс системы двух материальных точек (А; k1 (ед. массы)), (B; k2 (ед. массы)). Применим правило рычага (рис. 67) сначала для системы точек с центром К. Приходим к выводу:

АК : КВ = k2 : k1.

Затем сосредоточим всю массу системы двух точек (А; k1 (ед. массы)) и (B; k2 (ед. массы)) в центре масс этой системы – в точке К. Тогда точка О может рассматриваться как центр масс системы двух точек: (К; k2 + k1 (ед. массы)) и (С; k3 (ед. массы)). Пользуясь также правилом рычага, приходим к выводу, что

СО : ОК = k3 : (k2 + k1).

Задание 3 (max 15 баллов). С помощью сгибов разделите сторону квадратного листа бумаги на 9 равных частей. Обоснуйте правильность построений.

Критерии оценивания

Решение задания 3

Построение: Разделим сначала сторону квадрата на три части. Для этого сложим угол квадрата к середине противоположной стороны. В этом случае точка пересечения другой стороны, противоположной этому углу и стороне, прилегающей к нему, делит сторону квадрата в отношении один к двум (см. рис. 83).

Чтобы разделить сторону квадрата на девять частей, поступим аналогично, но угол квадрата сложим к точке, делящей сторону в отношении 2 : 1. В этом случае сторона угла разделится точкой перегиба в отношении 4 : 5. Разделить отрезок, равный 4 на четыре равные части не составляет труда – два раза пополам (см. рис. 84).

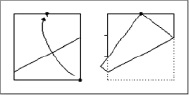
Рис. 83. Деление отрезка на три равные части

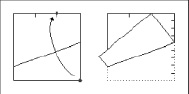
Рис. 84. Деление отрезка на четыре равные части

Обоснование: Пусть сторона квадрата равна 1. По теореме Пифагора для треугольника AGE (см. рис. 85) имеем: 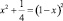. Отсюда получаем: x = 3/8. Рассмотрим далее треугольники AGE и BEF. Они подобны по двум углам. Составим пропорцию 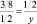, откуда 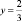. Аналогично, используя только теорему Пифагора, легко доказать отношение частей стороны квадрата, получаемое на втором шаге.

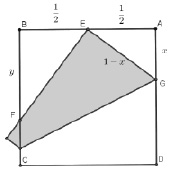
Рис. 85

Задание 4 (max 20 баллов). Панель инструментов GeoGebra состоит только из пяти инструментов: Точка 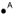, Отрезок по двум точкам 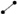, Луч по двум точкам , Окружность по центру и точке и Пересечение двух объектов . Решите следующую последовательность задач на построение в GeoGebra:

1) Построить правильный треугольник данными инструментами. Использовать результат решения задачи, чтобы дополнить панель инструментов своим инструментом Правильный треугольник. Сохранить файл под своей фамилией, например: Ivanov_4.1.ggb.

2) Убрать с панели инструментов инструмент Окружность по центру и точке. С помощью оставшихся инструментов построить произвольный отрезок и разделить его пополам. Использовать результат решения задачи, чтобы дополнить панель инструментов своим инструментом Середина отрезка. Сохранить файл под своей фамилией, например: Ivanov_4.2.ggb.

3) Убрать с панели инструментов инструмент Правильный треугольник. Добавить инструмент Окружность по центру и точке. Построить произвольную прямую и точку, не лежащую на ней. Провести через эту точку прямую, параллельную данной. Сохранить файл под своей фамилией, например: Ivanov_4.3.ggb.

4) С помощью имеющихся инструментов построить произвольный угол и его биссектрису. После чего дополнить панель инструментов своим инструментом Биссектриса. Сохранить файл под своей фамилией, например: Ivanov_4.4.ggb.

5) Построить окружность, вписанную в треугольник, имеющимися инструментами.

Сохранить файл под своей фамилией, например: Ivanov_4.5.ggb.

Критерии оценивания

Решение задания 4

1. См. решение задачи 4.1 для 7 класса.

2. См. решение задачи 4.2 для 7 класса.

3. См. решение задачи 4.3 для 7 класса.

4. С помощью имеющихся инструментов построить произвольный угол и его биссектрису. После чего дополнить панель инструментов
своим инструментом Биссектриса. Сохранить файл под своей фамилией, например: Ivanov_4.4.ggb.

Построить биссектрису угла можно двумя способами. С помощью инструмента Окружность по центру и точке необходимо выполнить следующие шаги:

а) Построить окружность с центром в точке А и произвольным радиусом.

б) Найти точки пересечения окружности со сторонами угла (точки В и С).

в) Построить окружность с центром в точке В и радиусом ВС.

г) Построить окружность с центром в точке С и радиусом ВС.

д) Найти точку пересечения этих окружностей (точка D).

е) Построить луч из вершины угла (луч AD) – биссектрису угла ВАС (см. рис. 86).

Затем создать инструмент согласно выданной на Турнире инструкции.

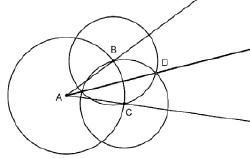
Рис. 86. Построение биссектрисы угла

Построение биссектрисы угла с помощью инструмента Середина отрезка описано на с. 158.

5. Построить окружность, вписанную в треугольник, имеющимися инструментами. Сохранить файл под своей фамилией, например: Ivanov_4.5.ggb.

Для того чтобы построить окружность, вписанную в треугольник, необходимо выполнить следующие шаги:

а) Построить произвольно треугольник с помощью инструмента Отрезок.

б) Провести биссектрисы с помощью полученного в задании 5 инструмента «Биссектриса».

в) Отметить точку пересечения биссектрис (точка D).

г) Построить две окружности с центрами в вершинах треугольника (точках А и С) и радиусами AD и CD соответственно.

д) Найти точку пересечения этих окружностей (точка Е).

е) Построить отрезок DE.

ж) Найти точку пересечения этого отрезка со стороной треугольника АС (точка F).

з) Построить окружность с центром в точке D и радиусом DF (рис. 87).

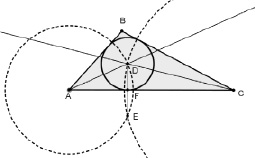
Рис. 87. Построение окружности, вписанной в треугольник

Задание 5 (max 30 баллов) (Задача составлена А.В. Ястребовым). Определить вид фигуры, которую образуют точки, равноудаленные от окружности произвольного радиуса и точки, лежащей вне этой окружности.

Решение задания 5. Пусть Х – одна из искомых точек. Для решения задачи необходимо сначала сформулировать определение расстояния от точки Х до окружности (А; r).

Определение. Расстоянием от точки Х, лежащей вне области ограниченной окружностью (А; r), до этой окружности будем называть внешнюю часть отрезка АХ, соединяющего эту точку с центром окружности, то есть отрезок СХ (см. рис. 35).

Построение. Это определение позволяет построить точку Х по следующему правилу:

1) Отметим на окружности произвольно точку С.

2) Проведем луч АС.

3) Построим геометрическое место точек, равноудаленных от точки С и В – серединный перпендикуляр к отрезку СВ.

4) Точка Х будет лежать на пересечении луча АС и серединного перпендикуляра.

Эксперимент. Введем для точки Х команду Оставлять след и будем перемещать точку С по окружности. Траекторией точки Х будет кривая, похожая на гиперболу (см. рис. 88).

Гипотеза: искомая фигура – гипербола.

Обоснование. Известно, что гипербола – это геометрическое место точек, абсолютное значение разности расстояний от которых до двух данных точек, называемых фокусами, постоянно. Примем за фокусы точки А и В. 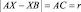, так как по построению треугольник СХВ – равнобедренный. Следовательно, гипотеза справедлива.

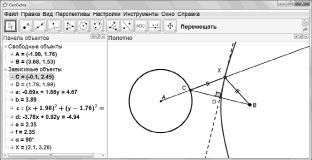
Рис. 88. Построение траектории точки Х с помощью команды Оставлять след

Задание 6 (по 10 баллов за каждую корректно поставленную задачу). Изменяя чертеж к заданию 5, составьте как можно больше новых задач. Формулировки своих задач можно записать или на листе бумаги, или в графическом окне GeoGebra с помощью инструмента – «Надпись».

Задачи, составленные путем изменения чертежа к задаче 5 (один из возможных наборов):

5.1. Определить вид фигуры, которую образуют точки, равноудаленные от окружности произвольного радиуса и точки, лежащей внутри этой окружности.

5.2. Определить вид фигуры, которую образуют точки, равноудаленные от окружности произвольного радиуса и точки, лежащей на этой окружности.

5.3. Определить вид фигуры, которую образуют точки, равноудаленные от двух окружностей разного радиуса. Исследуйте случаи различного взаимного расположения этих окружностей.

5.4. Определить вид фигуры, которую образуют точки, равноудаленные от данной окружности и прямой. Исследуйте все возможные случаи взаимного расположения окружности и прямой.

3.1.4. Итоги проведения первого турнира

В 2015 году в турнире приняли участие 68 учащихся, из них 24 – из школ г. Архангельска, 44 – из школ г. Северодвинска, г. Коряжмы Котласского района, школ Холмогорского и Верхнетоемского районов Архангельской области. Около 50 % учащихся, участвовавших в турнире, впервые воспользовались программой GeoGebra (30 чел.).

Итоги подводились отдельно по каждой базе проведения турнира (см. табл. 22):

(1) – Институт математики, информационных и космических технологий САФУ имени М.В. Ломоносова;

(2) – Средняя общеобразовательная школа № 24 г. Северодвинска;

(3) – Верхне-Матигорская средняя общеобразовательная школа Холмогорского района;

(4) – Корниловская СОШ Верхнетоемского района;

(5) – Средняя общеобразовательная школа № 1 г. Коряжмы Котласского района.

Таблица 22

Результаты первого областного турнира по Экспериментальной математике

Представленная таблица показывает, что результаты как подготовленных, так и неподготовленных учащихся достаточно низки. Это объясняется, главным образом, субъективной новизной предложенного способа деятельности. Экспериментальные методы находят весьма ограниченное применение в обучении математике. Если они и привлекаются к обучению математике, то в качестве методов, подводящих учащихся к открытию математических соотношений (теоремы о сумме углов треугольника, теоремы Пифагора и т.п.), а также при решениях задач в ситуациях, когда аналитические методы еще не известны учащимся (измерение площади фигуры палеткой, построение графиков функций по точкам и т.п.). Поскольку использование этих методов в математике носит эпизодический характер, и они играют роль вспомогательных, то опыт их применения у учащихся формируется только под влиянием лабораторных работ, проводимых при изучении дисциплин естественно-научного блока. Одной из целей проведенного турнира по Экспериментальной математике явилось выявление возможностей переноса навыков применения экспериментальных методов, освоенных в курсах физики, химии, биологии на решения математических задач в отсутствии специального обучения этим методам на уроках математики.

Первая задача турнира провоцировала столкновение в сознании учащихся противоречивости знаний о равновеликости равносоставленных планиметрических фигур, полученных на уроках математики теоретически, с результатами экспериментальных действий. Учащиеся должны были объяснить несоответствие теории и практики. Анализ работ учащихся показал, что все полученные результаты можно разделить по трем группам. В первую группу попадают работы учеников, склонных безгранично доверять экспериментам, подгоняя теорию под результаты экспериментов и признавая ложным то, что противоречит экспериментальным данным. Примером этой позиции является решение первой задачи, представленное на рис. 89.

Рис. 89. Позиция безграничного доверия экспериментам

Представители другой группы показали, что безгранично доверяют положениям теории, подгоняя под нее данные эксперимента или вовсе отказываясь от его проведения. Пример этой позиции представлен на рис. 90.

Рис. 90. Позиция безграничного доверия теории

Третью группу составили учащиеся (их количество оказалось очень незначительным), которые понимают, что выводы, основанные на теоретических фактах и экспериментальных данных должны быть согласованы. Пример описания решения задачи 1 представителя этой группы представлен на рис. 91.

Рис. 91. Позиция согласованности экспериментальных данных
с теоретическими фактами

Вторая задача была направлена на проверку умений планировать физический эксперимент применительно к ситуации, описанной на языке математики. Предполагалось, что учащиеся в этой деятельности будут опираться на знания, полученные в курсе физики, о расположении центра масс системы материальных точек или на правило рычага (оно было актуализировано у учащихся рисунком, расположенным под условием задачи). Однако никто из учеников не воспользовался этой подсказкой. Те из них, кто справился с задачей, предложили разрезать фигуру на части и взвесить их. Затем доказали, опираясь на математические знания, что отношение исследуемых отрезков равно отношению масс частей фигуры, их содержащих (см. рис. 92).

Рис. 92. Одно из решений второго задания участниками турнира

Третья задача проверяла умение применять метод оригами к решению задач на основе знаний, приобретенных в курсе математики. Для того чтобы при решении задачи, учащиеся не пользовались отношением параллельности и перпендикулярности краев листа, линиями его разметки, им выдавались белые листы с неровными краями.

Эта задача оказалась самой простой для восьмиклассников. Ее решили практически все участники. Для учащихся 7 класса эта задача оказалась неожиданно трудной. Им оказалось трудным работать
в отсутствии образа самой окружности или хотя бы ее дуги. Для воссоздания образа окружности они выполняли дополнительные построения, используя при этом криволинейные края листа (см. рис. 93).

Рис. 93. Одно из решений третьего задания участниками турнира

Ученикам оказалось непросто при решении четвертой задачи именно в построении объектов ограниченным набором инструментов. Причем факт, что сами инструменты были виртуальными, не вызвал сложности у учащихся, тем более, что организаторы турнира предоставили им возможность пользоваться инструкциями по управлению панелью инструментов и созданию своего инструмента GeоGebra. Школьники легко справились лишь с теми задачами, для построения которых требовалось воспользоваться инструментами сходными с циркулем и линейкой (см. рис. 94).

Сложности возникли на третьем уровне, когда принципы использования набора инструментов перестали быть очевидными. Большинство учащихся после нескольких бесплодных попыток подобрать нужные построения ограничивались построением динамически неустойчивой конструкции, используя возможность перемещения объектов для «подгонки» результата под заданные параметры (см. рис. 95).

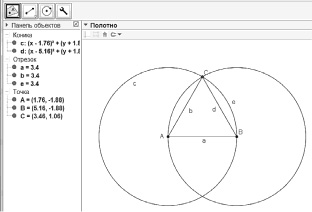
Рис. 94

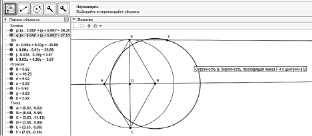
Рис. 95

Пятая задача потребовала привлечения мысленных или компьютерных экспериментов. Однако опыт компьютерных построений, приобретенный учащимися, при решении предыдущей задачи оказался недостаточным для построения динамически устойчивой модели объекта исследования. Это привело их к неверным гипотезам
(см. рис. 96). Никто из участников турнира даже не попытался дать теоретическое обоснование или объяснение выдвинутой гипотезе о виде геометрического места точек.

Полученные данные еще раз доказывают необходимость целенаправленного формирования у учащихся правильных представлений о роли и месте теоретических и экспериментальных методов в математической деятельности, а также умений рационально использовать сочетание этих методов.

Несмотря на то, что решить задачу 5 оказалось многим не под силу, попытку составить свои задачи на ее базе сделали многие участники турнира, некоторые из них использовали для этих целей и модифицирующие возможности GeoGebra (см. рис. 97).

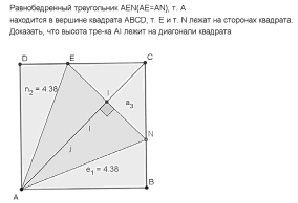
Рис. 97

Наиболее типичными способами составления задач являлась модификация конструктивного объекта.

Подводя итог представленному анализу результатов первого турнира по экспериментальной математике следует отметить, что это соревнование может быть использовано не только в качестве формы работы, позволяющей привлечь учащихся к изучению экспериментальных методов и средств экспериментальной математики, но также и в качестве диагностического средства оценки степени подготовленности учащихся к применению этих методов и средств в процессе познания.