Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

3.2. Создание виртуальных лабораторий и динамических тренажеров учащимися

В этом параграфе мы опишем опыт включения учащихся в проектную деятельность, направленную на создание собственных интерактивных электронных образовательных ресурсов в среде GeoGebra. Такая работа более полезна, чем использование готовых ресурсов, так как в ходе ее выполнения у учащихся формируется опыт проектно-исследовательской деятельности, а также повышается уровень предметных результатов обучения.

3.2.1. Создание учащимися виртуальных лабораторий по теме «Интерференция волн» как способ интеграции знаний учащихся по физике, математике и информатике

Готовые виртуальные лаборатории по физике для школьников сегодня предлагают многие компьютерные кампании. Хорошо известны такие ресурсы как «1С: Лаборатория», «Живая физика», VirtuLab, SenseDisс Physics и другие.

Наиболее часто виртуальная лаборатория представляет собой «рабочий стол», на котором обучающийся с помощью специализированных программ может моделировать объект исследования, имитировать процесс проведения лабораторного исследования с помощью виртуальных измерительных инструментов.

Пример 1. Виртуальная лаборатория для проведения работы на тему «Прибор Атвуда. Проверка Второго закона Ньютона».

Ресурс (см. рис. 98) включает модель лабораторной установки, описание назначения установки и цели лабораторной работы, инструкцию по проведению опытов, а также инструменты для управления опытом: «Запустить», «Остановить», «Привести в исходное состояние».

При наличии этого ресурса лабораторная работа учащихся наиболее часто включает три этапа:

– подготовительный, на котором учащиеся актуализируют знания Второго закона Ньютона, знакомятся с назначением, историей создания и устройством прибора Атвуда, виртуальной лабораторией, осваивают способ ее использования для проверки закона;

– основной, на котором учащиеся имитируют свои действия по проведению лабораторного эксперимента на приборе Атвуда;

– заключительный, на которому учащиеся делают выводы о справедливости закона на основе полученных экспериментальных данных.

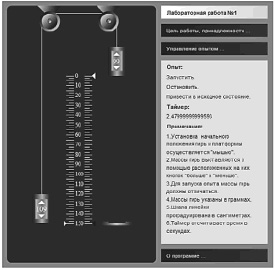
Рис. 98

При таком использовании работа с реальным прибором Атвуда заменяется работой с ее виртуальной моделью, созданной на основе представлений об идеальной машине Атвуда (нить, переброшенная через блок, невесома и нерастяжима; блок невесом; если массы тел равны, то вне зависимости от их положения система находится в состоянии равновесия, если не равны, то система тел приходит в поступательное движение). В результате использования виртуального прибора, учащиеся получают данные, которые далеки как по своим характеристикам, так и по своей природе от экспериментальных. Они получены методом компьютерных вычислений (скрытых от учащихся), и потому, повторение опыта в одних и тех же заданных условиях не меняет значения измеряемых величин.

В связи с этим подмена реальных лабораторных работ их компьютерной имитацией не только обедняет образовательные результаты,
состоящие в формировании умений, относящихся к экспериментальному способу познания, но часто и искажает их. По этой причине учителя не спешат перейти на использование готовых виртуальных лабораторий, несмотря на очевидную возможность сэкономить финансовые ресурсы школы и учебное время.

Мы предлагаем не отказываться от использования виртуальных лабораторий в процессе обучения, а вовлекать учащихся в деятельность их создания, мотивированную сложностью или даже невозможностью постановки натурного эксперимента, возможностью использовать созданный ресурс для поддержки решения задач.

Пример 2. Постановка проектного задания на создание виртуальной лаборатории «Интерференция волн» средствами GeoGebra.

Для создания мотивирующей ситуации проектное задание включает все необходимые теоретические сведения по интерференции волн, а также практические задания на проведение наблюдений интерференции в двух случаях:

1) механических волн, возникающих на поверхности воды при наличии двух источников вибрации;

2) световых волн, возникающих при использовании бипризмы Френеля.

После выполнения подготовительных работ учащимся предлагается создать инструментами GeoGebra ресурс – виртуальную лабораторию, позволяющий моделировать интерференционную картину, возникающую в результате наложения волн длиной , исходящих от двух источников монохроматического света, которые расположены на расстоянии h друг от друга и удалены от экрана на расстояние s.

В качестве средства оказания учащимся дозированной помощи в выполнении этого задания выступает инструкция по созданию виртуальной лаборатории. Ее содержание должно быть по возможности индивидуализировано и согласовано с зонами актуального и потенциального развития учащихся. Очевидно, что на практике речь может идти только о дифференциации. Мы предлагаем исходить из предположения, что учащиеся обладают относительно одинаковым уровнем подготовленности при изучении темы «Интерференция волн» (для этого момент постановки проектного задания совмещают со временем изучения данной темы). Однако могут иметь разный уровень базовых знания по математике и информатике. Таким образом, инструкции должны быть составлены так, чтобы предоставлять учащимся в случае необходимости восполнить пробелы в базовых знаниях.

Шаг 1. Для создания интерференционной картины в графическом поле GeoGebra надо задать четыре параметра. Три из них указаны в условии задачи, а четвертым будет m – порядок отображаемого интерференционного максимума. Области изменения значений параметров выбираются следующими: [3,8; 7,8] c шагом 0,05; h [0; 5] с шагом 0,1; s [10; 20] c шагом 0,1; m [–30; 30] c шагом 1.

Итог этой работы представлен на рисунке (рис. 99).

Задание параметра [3,8; 7,8] c шагом 0,05 позволит задавать длины волн в 100 нм и рассматривать волны всех цветов спектра: фиолетового (380–440 нм), синего (440–480 нм), голубого (480–510 нм), зеленого (510–550 нм), желтого (575585 нм), оранжевого (585–620 нм), красного (620–780 нм).

Рис. 99

Примечание (для начинающих пользователей GeoGebra). Для задания параметра необходимо воспользоваться инструментом «ползунок». Выбрав его на панели инструментов нужно нажать на желаемое место расположения в графическом окне. Появится диалоговое окно (см. рис. 100). Оно позволяет выбрать нужное имя параметра, указать область его изменения и выбрать шаг изменения.

Шаг 2. Получить динамическое изображение взаимного расположения источников и экрана, определенное текущими значениями h и s. Цвет источников должен также быть динамичным, т.е. изменяться в зависимости от значений ?. Результат этого шага представлен на рисунке (рис. 101).

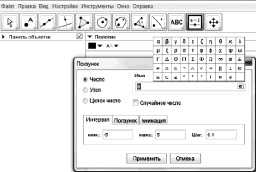
Рис. 100

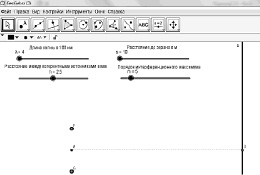
Рис. 101

Примечание (для начинающих пользователей GeoGebra). Динамическая окраска объектом может быть получена путем задания дополнительных свойств построенного объекта. Для этого нужно, указав объект, вызвать диалоговое окно и войти во вкладку «Свойства». Далее имеется две возможности:

1) задать нужный цвет объекта, а затем, используя опцию «Дополнительно», задать условия его отображения; затем создать такой же объект, но другого цвета, и задать новые условия его отображения;

2) выбрав опцию «Дополнительно», указать промежутки значений параметра от которого зависит окраска объекта (этот способ позволяет варьировать лишь красный, зеленый и синий цвета).

Шаг 3. Построение точки, указывающей положение интерференционного максимума, порядок которого определяется текущим значением m, требует выражения его расстояния от нулевого максимума через заданные параметры.

Идея расчета видна из рис. 102, на котором изображена интерференция от двух когерентных источников.

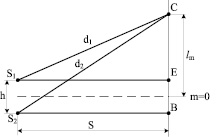
Рис. 102

Запишем условие максимума для некоторой точки С на экране:

d = m,

где d – геометрическая разность хода; m – целое число, порядок максимумов; – длина волны.

d = d2 – d1,

где d1 – расстояние, проходимое волной от первого источника до m-го максимума; d2 – расстояние, проходимое волной от второго источника до m-го максимума.

Воспользуемся теоремой Пифагора. Из треугольников S1CE и S2СB выразим:

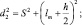(1)

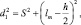(2)

где s – расстояние от экрана до линии, соединяющей источники когерентных волн; h – расстояние между источниками; lm – расстояние от нулевого максимума до максимума m-го порядка.

Вычитаем почленно из равенства (1) равенство (2) и выполняем преобразования

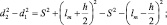
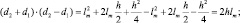
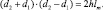
2S d2 + d1, так как h << S, d = d2 – d1, 2Sd = 2hlm. 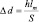, так как d = m, 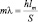, отсюда получаем формулу, выражающую расстояние точки m-го максимума от нулевого максимума: 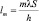(100 нм).

Эта формула позволяет построить изображение на экране точки m-го максимума интерференции волн.

Примечание 1 (для начинающих пользователей GeoGebra). Построить точку m-го максимума можно с помощью инструмента «Окружность по центру и радиусу». В качестве центра окружности выбирается точка О – место положения нулевого максимума, радиус задается как вычисляемая переменная: 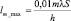(см. рис. 103).

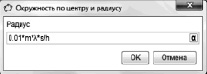
Рис. 103

Для получения интерференционной картины, на которой отображены максимумы, достаточно для построенной точки ввести функцию «Оставлять след», а затем пробежать все значения m (см. рис. 104).

Рис. 104

Аналогичным образом может быть получена интерференционная картина с изображением минимумов. Для построения точек минимума необходимо воспользоваться формулой:

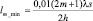(100 нм).

Шаг 4. Построить изображение самих волн. Для этого необходимо сначала рассчитать формулу, задающую синусоиду, которая будет изображать волну. Используем формулу электромагнитной волны:

x = Asin ;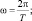

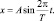
Выразим период колебаний через длину волны:

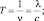
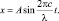
Для того, чтобы отображалась лишь часть синусоиды, соответствующая длине луча, необходимо ввести ограничения на область изменения аргумента функции для волны каждого цвета. Затем подвергнуть каждый из отрезков синусоиды геометрическим преобразованиям (см. рис. 105).

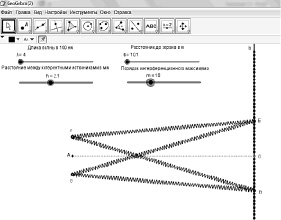
Рис. 105

Примечание (для начинающих пользователей GeoGebra). Задать ограничение области изменения аргумента функции можно с помощью логической формулы. Например, для волны фиолетового цвета нужно построить два фрагмента, со следующими ограничениями:

Если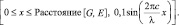

Если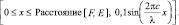

Для определенности примем, что А = 0,1 мкм, скорость света с 3*108 м/с. На чертеже F – точка, определяющая место положение одного из источников фиолетового света, E и D – точки, изображающие максимум интерференции m-го порядка.

Примечание (для школьников, имеющих математические трудности). Для получения изображения световой волны необходимо отрезок синусоиды подвергнуть двум преобразованиям:

1) сначала совместить начало синусоиды (точку А) с источником света (например, с точкой F), для этого осуществить параллельный перенос на вектор с началом в точке А и концом в точке, изображающей источник света (например, на вектор );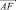

2) затем осуществить поворот синусоиды вокруг источника света на нужный угол (например угол между АО и FE).

Для создания изображения всего спектра цветов необходимо повторить шаги 2–6 семь раз, задавая соответствующий цвет и условия отображения источникам, точкам максимума и синусоидам.

После того, как виртуальная лаборатория готова учащимся предлагается с ее помощью решить следующие задачи.

1. Два когерентных источника S1 и S2 излучают монохроматический свет с длиной волны 600 нм. Определить, на каком расстоянии от центрального максимума на экране будет первый максимум освещённости, если S = 4 м и h = 1 мм.

2. Голубые лучи с длиной волны 480 Нм от двух когерентных источников, расстояние между которыми 120 мкм, попадают на экран. Расстояние от источников до экрана равно 3,6 м. В результате интерференции на экране получаются чередующиеся тёмные и светлые полосы. Определить расстояние между центрами соседних тёмных полос на экране. Каким будет это расстояние, если голубые лучи заменить оранжевыми с длиной волны 650 нм?

3. Когерентные источники белого света, расстояние между которыми 0,32 мм, имеют вид узких щелей. Экран, на котором наблюдается интерференция света от источников, находится на расстоянии 3,2 м от них. Найдите расстояние между красной (длина волны 760 нм) и фиолетовой (длина волны 400 нм) линиями второго интерференционного спектра.

4. Две узкие щели расположены так близко друг к другу, что расстояние между ними трудно установить прямыми измерениями. При освещении щелей светом с длиной волны 5*10–7 м оказалось, что на экране, расположенном на расстоянии 4 м от щелей, соседние светлые полосы интерференционной картины отстоят друг от друга на 2 см. Каково расстояние между щелями?

3.2.2. Создание учащимися динамических тренажёров для подготовки к государственному выпускному экзамену по математике

Традиционно подготовка учащихся к сдаче основного государственного экзамена по математике основана на организации их деятельности по решению задач открытого банка экзаменационных заданий, размещенных на сайте ФИПИ [141] и включенных в соответствующие сборники.

Мы предлагаем другой путь – включение учащихся в деятельность создания собственных дидактических материалов средствами GeoGebra.

Анализ контрольно-измерительных материалов ОГЭ по математике показывает, что целесообразно организовать деятельность учащихся вокруг создания тренажеров трех видов (см. табл. 23).

Таблица 23

Приведем примеры инструкций, которые предлагались учащимся для выполнения проектных заданий по созданию тренажеров этих видов.

Пример 1. Создайте средствами GeoGebra тренировочный тест, содержаний задания на проверку истинности утверждений:

«Для каждого утверждения установите, истинное оно или ложное:

1. Каждая сторона треугольника меньше суммы двух других сторон.

2. В равнобедренном треугольнике отрезок, соединяющий любую точку основания, отличную от вершины, с противоположной вершиной, меньше боковой стороны.

3. Если два угла равны, то они являются вертикальными.

4. Если углы вертикальные, то они равны».

Тест должен содержать средства для предварительной проверки правильности выбора ответа, а также включать счетчик правильных ответов (см. рис. 106).

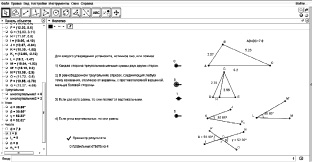
Рис. 106

Инструкция

Шаг 1. Создайте перечень утверждений с помощью инструмента Текст .

Шаг 2. Создайте средства выбора ответа для каждого утверждения. Для этого выберите на панели инструмент Ползунок . Параметр ni должен принимать три значения: 0 – ложь, 1 – истина, 2 – не знаю.

Шаг 3. Создайте средства визуальной проверки утверждений. Например, средством проверки первого утверждения может служить динамическое изображение треугольника c выведенными на экран значениями длин сторон. Для простоты наблюдений с помощью строки ввода полезно создать переменные, равные сумме длин каждой пары сторон.

Поскольку визуальная проверка нужна только при неправильном выборе учащегося, то необходимо задать в качестве условия их отображения нa экране значения ni, соответствующего неверному ответу. Например, для первого утверждения нужно задать ni = 0.

Шаг 4. Создайте счетчик правильных ответов. Для того, чтобы правильным ответам соответствовал всегда 1 балл, задайте логическую функцию, которая будет сопоставлять правильному ответу на третий вопрос 1, в остальных случаях – 0: y = Если [n3 = 0,1,0]. Затем, создайте переменную s, равную сумме n1 + n2 + y. Для вывода ее в графическое поле создайте текст: «s правильных ответов из 4». Для того, чтобы этот результат не был виден сразу, используйте инструмент Флажок .

Пример 2. Создайте средствами GeoGebra динамический генератор однотипных задач с заданным прототипом:

«В равнобедренном треугольнике основание равно 16 см, а боковая сторона – 10 см. Вычислите радиус вписанной и описанной окружностей и расстояние между их центрами».

Подсказка. Для получения обобщенной задачи замените числовые данные параметрами: «В равнобедренном треугольнике основание равно а, а боковая сторона – b. Вычислите радиус вписанной и описанной окружностей, и расстояние между их центрами».

Генератор задач должен включать динамическое условие, чертеж, подсказки и ответ, которые выводятся на экран по мере необходимости (см. рис. 107).

Рис. 107

Инструкция

Шаг 1. Создайте два ползунка a и b. Пусть область изменения параметра а от 0 до 10 с шагом 0,1; область изменения параметра b от а/2 до 15 с шагом 0,1.

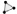Шаг 2. Постройте равнобедренный треугольник с основанием b и боковыми сторонами а, пользуясь инструментами: Отрезок фиксированной длины , Окружность по центру и радиусу , Пересечение двух объектов , Многоугольник (см. рис. 108).

Вспомогательные элементы можно убрать с экрана.

Рис. 108. Построение равнобедренного треугольника

Шаг 3. Для построения описанной окружности надо воспользоваться инструментом Окружность по трем точкам . Центр этой окружности может быть построен с помощью инструмента Середина или центр .

Шаг 4. Для построения вписанной окружности нужно построить две биссектрисы инструментом Биссектриса угла , затем отметить точку их пересечения инструментом Пересечение двух объектов . Получим центр окружности. Затем с помощью инструмента Середина или центр нужно отметить середину основания равнобедренного треугольника. Вписанная окружность может быть построена инструментом Окружность по центру и точке .

Шаг 5. Радиусы вписанной и описанной окружности, а также расстояние между их центрами может быть измерено инструментом Расстояние или длина .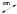

Шаг 6. Для создания текста с условием задачи воспользуйтесь инструментов Надпись (см. рис. 109).

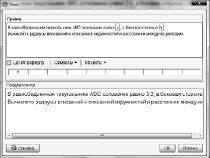
Рис. 109

Шаг 7. Для того, чтобы скрыть ответ задачи воспользуйтесь инструментом Флажок .

Шаг 8. Для того чтобы дополнить задачу списком необходимых для ее решения формул, создайте еще одну надпись. Для того чтобы формулы имели привычный вид, поставьте флажок вкладки «LaTeX-формула» и пользуйтесь ниспадающим списком (см. рис. 110).

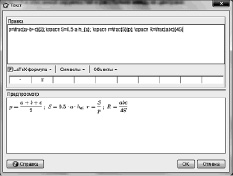
Рис. 110

Шаг 9. Для того чтобы решающие видели, что нахождение расстояния между центрами окружностей зависит от вида треугольника, можно создать визуальную подсказку: изобразить отрезки FG – расстояние между центрами, FC – радиус описанной окружности и GE – радиус вписанной окружности (см. рис. 111).

Шаг 10. Скрыть формулы и визуальную подсказку можно снова с помощью инструмента Флажок .

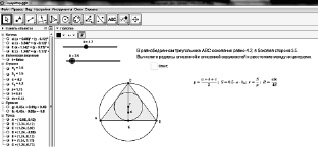
Рис. 111

Пример 3. Создайте средствами GeoGebra динамический модификатор задачи: «В прямоугольнике АВСD биссектриса угла А пересекает сторону ВС в точке К. Найдите длину отрезка АК, если AD = 11, а периметр АВСD равен 38».

Модификатор должен содержать условия модифицированных задач, а также ответы для самопроверки их решения (см. рис. 112).

Инструкция

Шаг 1. Создайте в графическом окне три ползунка:

а – отвечает за длину стороны AD прямоугольника АВСD; его минимальное значение 1, максимальное – 20, шаг – 1.

P – отвечает за изменение периметра прямоугольника АВСD; его минимальное значение – 15, максимальное – 80, шаг – 1.

-отвечает за изменение угла А; его минимальное значение – 0°, максимальное – 180°, шаг – 1°.

Придайте ползункам значения, соответствующие условию задачи (а = 11, Р = 38, = 90°), и начните построение описанных в условии задачи объектов.

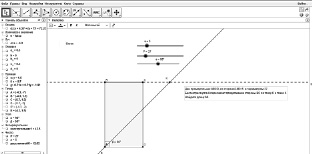
Рис. 112. Модификатор задач

Шаг 2. Постройте сторону AD длины а с помощью инструмента Отрезок фиксированной длины .

Шаг 3. Постройте угол DAB величины ? с помощью инструмента Угол заданной величины .

Шаг 4. Проведите луч AD, и с помощью инструмента Окружность по центру и радиусу сделайте на нем засечку на расстоянии от А, равном длине второй стороны прямоугольника.

Шаг 5. С помощью инструментов Пересечение двух объектов , Параллельная прямая и Многоугольник завершите построение АВСD (см. рис. 113).

Шаг 6. С помощью инструмента Биссектриса угла постройте биссектрису угла А.

Шаг 7. С помощью инструмента Пересечение двух объектов постройте точку пересечения биссектрисы угла А и прямой (покажите на прямую за пределами отрезка ВС), на которой лежит сторона ВС. Переименуйте ее в точку К.

Шаг 8. Измерьте длину отрезка АК инструментом Расстояние или длина .

Шаг 9. Спрячьте ответ с помощью инструмента Флажок .

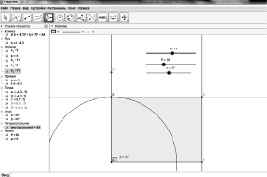
Рис. 113. Построение четырехугольника

Шаг 10. С помощью инструмента Надпись создайте тексты, соответствующие всем возможным формулировкам задач-модификаций. Для полученной надписи откройте диалоговое окно и, пройдя во вкладку Дополнительно, задайте условия отображения нужного текста.

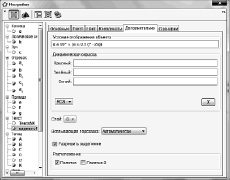
Рис. 114. Окно дополнительной настройки отображения текста

Например, условием отображения задачи «Дан прямоугольник АВСD, его сторона AD = a, а периметр P. Биссектриса угла А пересекает сторону ВС в точке К. Найдите длину АК». Имеем условие, представленное на рисунке ниже (рис. 114).

Данную работу целесообразно организовать в форме коллективного проекта (каждый учащийся или микрогруппа) работает над своим набором тренажеров, затем передает свой набор другой группе для тестирования. Созданная классом в результате этого проекта коллекция тренажеров может быть использована в учебном процессе или самостоятельной работе учащихся для подготовки к экзамену.