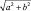Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

3.3. Лабораторные работы по математике с GEOGEBRA

Лабораторные работы широко используются в практике обучения дисциплинам естественнонаучного блока (физике, химии, биологии). Они представляют собой практические занятия, в ходе которых учащиеся индивидуально или в группах ставят эксперименты с целью практического освоения теории, приобретения опыта экспериментальной работы, овладения навыками работы с приборами и др.

Проведенный нами анализ текстов лабораторных заданий, предлагаемых в различных учебных пособиях по этим дисциплинам, показал, что все эксперименты, которые предлагается поставить учащимся, носят конфирматорный характер, т.е. направлены на проведение экспериментов, подтверждающих ранее введенные теоретические положения. Приведем в подтверждение пример одной из лабораторных работ, имеющейся в тексте учебника физики [69] (см. рис. 115).

Пример 1.

В отличие от физики, химии, биологии обучение математике не предусматривает организацию и проведение лабораторных работ. Хотя вопрос о возможности и целесообразности проведения лабораторных работ по математике поднимался в методике обучения математике неоднократно в связи с усилением прикладной и практической направленности обучения. Так, например, к периоду Колмогоровской реформы (70-е годы XX века) относится методическая разработка Ф.И. Яковлева, Д.М. Кирюшкина и Г.В. Воробьева [102], в которой предложено большое количество лабораторно-практических работ по разным темам школьного курса математики. Однако увлечение новыми идеями обучения математике, связанными с внедрением аксиоматического подхода,
с абстрактными теоретическими построениями, широким использованием теоретико-множественных представлений и логического языка, сделало невозможным распространение в широкой педагогической практике предлагаемых работ. Благоприятные условия сложились в период контрреформы (80-е годы XX века). Тогда в практику учебной работы школы и, соответственно, в систему подготовки учителей математики в вузах были введены измерительные работы на местности (элементы геодезических измерений). Некоторые авторы данного параграфа являлись непосредственными участниками этих экспериментов и имели возможность оценить это новшество с позиций ученика, а затем и студента. Работы выполнялись в рамках бригадной формы организации занятий и занимали два академических часа. Первый час – инструктаж и измерение на местности с использованием геодезического оборудования. Второй час – анализ собранных данных, составления отчета. Эти работы были мало эффективны, это было очевидно даже ученикам. Во-первых, подготовка учащихся к использованию специализированного оборудования и специальных методов анализа данных требовала много времени. Во-вторых, закупка такого оборудования и поддержание его в рабочем состоянии была сопряжена с немалыми затратами. В-третьих, бригадный метод предоставлял большинству учащихся возможность пассивного участия и/или выполнения заданий, не имеющих ни прямого, ни косвенного отношения к математике. Эти причины обусловили довольно быстрое «исчезновение» лабораторно-практических работ по математике из школьной практики. Тогда же появились новые «модные» формы обучения математике, связанные с применением тестовых устройств.

Вновь интерес к лабораторным и практическим работам по математике возник в годы перестройки и демократической реформы системы образования (90-е годы ХХ века – начало ХХI века). В этот период в журнале «Математика в школе» было опубликовано множество статей, посвященных разработке лабораторных и практических работ, связанных с различной тематикой, и описанию достоинств этих видов организации учебной работы. Приведем некоторые из них:

– лабораторные работы по стереометрии, как метод развития пространственного мышления учащихся в процессе моделирования фигур, построения их разверток, постановки и решения вычислительных задач на основе измерения (Т. И. Симакова [82]);

– лабораторные работы для пропедевтического изучения геометрии в 1–6 классах (Л.П. Котельникова [45], Р.К. Фахрутдинова [48], Л. Кокорева [92]);

– лабораторные работы для вовлечения учащихся в деятельность исследовательского характера, связанную со сбором фактов для формулировки утверждений посредством индуктивных выводов, самостоятельного открытия теоретических положений (Р. Кашаева, А. Конакош [43], А.А. Окунев [66]; М.В. Шабанова [95]);

– лабораторно-графические работы для формирования измерительных и конструктивных навыков, применения правил приближенных вычислений (А. Морозова [59]; Н. Андреева [9]).

Результатом этих предложений учителей и ученых явилось введение некоторыми авторами школьных учебников лабораторных работ в программы по математике. Например, в курс математики для 5–6 классов [63], в курс алгебры и начал анализа для 10–11 классов [17]).

Однако по-прежнему в школьной практике лабораторные и практические работы по математике являются одной из наиболее редко применяемых форм работы. Особенно редки лабораторные работы при изучении систематических курсов алгебры, геометрии, алгебры и начал математического анализа. Объяснение этому мы нашли в ответах учителей математики на вопрос о причинах их отказа от использования таких видов работ. Отказ от проведения лабораторных и практических работ объясняется соображениями экономии учебного времени, а также причинами, связанными с трудностями организации самого процесса сопровождения деятельности ученика, каждый из которых по-своему дисциплинирован, имеет свои психофизиологические и психоэмоциональные особенности, свой темп работы и т.д. При этом многие учителя отдают должное дополнительным образовательным возможностям, которые предоставляются как самим процессом выполнения лабораторных и практических работ, так и их результатом. Отказываясь от организации и проведения лабораторных и практических работ на уроке, учителя все же используют их для постановки домашних заданий.

Обобщая опыт внедрения лабораторных работ в практику учебной работы, учитывая и множественные неудачные попытки такого внедрения, видим, что в системе общего математического образования вновь назрел момент, когда целесообразно переосмыслить с новых позиций накопленный опыт постановки лабораторных заданий и организации такой работы с учащимися с учетом идей экспериментальной математики. Это связано с информатизацией математического образования, включением в систему требований ФГОС ООО и ФГОС С(П)ОО требований формирования умений применять компьютерную технику для решения математических задач, проникновением в школу идей экспериментальной математики.

Крайне важно определиться с пониманием сути понятия «лабораторная работа по математике», главным образом, для правильного отражения содержанием работ методологии экспериментальной математики. Разумеется, существуют риски и опасения, связанные с немотивированным использованием компьютерных средств. Опасность включения в школьные учебники заданий на применение компьютера без предварительного обсуждения продемонстрируем на учебниках-«пионерах» информатизации (авторский коллектив Г.К. Муравин, О.В. Муравина).

Итак, пример типичного задания на применение компьютерных средств.

Пример 2 (задание № 39 [60]): «Напишите уравнения касательных к графику функции y = 2x2 – x + 3, проходящих через точку:

а) А (–1; 6);

б) D (0; 3) ».

Символ означает, что задание под буквой б) авторы рекомендуют учащимся решить с использованием компьютера. Программа GeoGebra (рекомендованная авторами) позволяет выполнить это задание следующим образом:

1) построить график функции y = 2x2 – x + 3, записав уравнение в строке ввода;

2) отметить в графическом окне точку D (0; 3), для этого координаты точки также задаются с помощью строки ввода; 3) построить касательную к графику функции, проходящую через точку D с помощью инструмента «касательная». На панели объектов и в самом графическом окне автоматически появится уравнение построенной касательной (см. рис. 116).

Как видно из представленного описания, такое решение задачи вовсе не требует от учащихся знаний об общем виде уравнения касательной к графику функций, умения находить производную функции в точке, определять является ли заданная точка точкой касания. Уровень сложности задания под буквой б) не отличается от уровня сложности задания под буквой a). В связи с этим мотив обращения к компьютеру, как к средству решения задачи, вызывает недоумение, сомнительны образовательно-ценностные выводы, к которым должны прийти учащиеся по результатам сравнения аналитического и компьютерного способов решения задач. Такой подход к организации практической деятельности ученика может и будет провоцировать устойчивое неприятие идей экспериментальной математики профессиональным педагогическим сообществом.

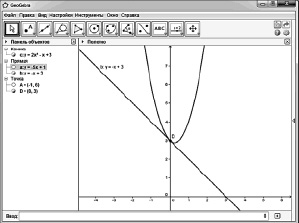
Рис. 116. Решение примера 2

Компьютерный лабораторный практикум по математике, по нашему мнению, должен включать лишь те задания, которые не могут быть решены с применением одних аналитических методов, осваиваемых школьниками на уровне базовых знаний.

В связи с тем, что экспериментальные методы сегодня используются на самых разных этапах математических исследования, мы считаем возможным и целесообразным не ограничиваться постановкой заданий на проведение конфирматорных экспериментов. Полезно и важно говорить о возможности организации лабораторных работ, имеющих различные образовательные цели. В зависимости от образовательных целей и учебной ситуации полезными для практики обучения математике могут оказаться как лабораторные работы с вещественными моделями математических объектов, так и лабораторные работы с виртуальными моделями. В некоторых случаях целесообразно использовать их сочетания.

Мы выделяем несколько видов лабораторных работ (которые вполне согласуются с традиционной терминологией):

– лабораторно-исследовательские работы, направленные на проведение учащимися компьютерных экспериментов с целью выдвижения гипотез:
о существовании и видах математических объектов, обладающих указанным в условии исследовательской задачи набором свойств; об общих свойствах математических объектов, составляющих объем изучаемого математического понятия; о закономерных связях свойств математических объектов;

– лабораторно-иллюстративные работы, направленные на проведение учащимися экспериментов с целью подтверждения математических положений: осмысление математических правил с точки зрения правил практических действий; адекватность результатов, получаемых по вычислительным формулам, результатам непосредственных измерений; возможность конструирования моделей математических объектов, на которые распространяются положения;

– лабораторно-практические работы, направленные на проведение учащимися экспериментов с целью овладения практическими навыками: использования конструктивных и измерительных инструментов; разработки способов практических действий, основанных на математических положениях; оценки правдоподобия результатов практических действий с использованием математических положений;

– обобщающие лабораторные работы, направленные на проведение учащимися экспериментов с целью систематизации и обобщения изученного в ходе: разработки практических способов распознавания моделей объектов, принадлежащих родственным математическим понятиям; создания модели-трансформера, принимающего вид разных математических объектов (известных и новых); получения новых фактов, объясняемых на основе имеющихся математических знаний.

Для сравнения приведем примеры лабораторных работ, проводимых с вещественными и с виртуальными моделями в программе GeoGebra.

Пример 3. Лабораторно-исследовательская работа на тему «Определение вида треугольника».

Цель: сформулировать признак для определения вида треугольника по соотношению длин его сторон.

Постановка задачи: Теорема Пифагора гласит, что, если треугольник АВС – прямоугольный, то a2 + b2 = c2, где a, b, c – длины его сторон.

Данное утверждение приводит к постановке естественных вопросов: «Верно ли обратное утверждение?», «Какой вид будет иметь треугольник, если a2 + b2 > c2 или a2 + b2 < c2, при условии, что a b c Ответ на эти вопросы Вам предстоит найти экспериментально.

Вариант 1 (без использования компьютера)

Ход работы.

1. Изобразите два отрезка произвольной длины. Измерьте их линейкой. Запишите результаты измерений. Обозначьте за b отрезок большей длины, за a – отрезок меньшей длины. Вычислите .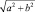

2. С помощью линейки постройте отрезок с:

1) равный вычисленному значению;

2) больший b, но меньший вычисленного значения;

3) больший вычисленного значения, но меньший суммы а и b.

3. Для всех трех вариантов постройте циркулем и линейкой треугольник со сторонами а, b и c.

4. Измерьте транспортиром угол против стороны с.

5. Занесите свои экспериментальные данные и выводы в сводную таблицу результатов:

6. Сделайте вывод о виде треугольника (для каждого случая).

Вариант 2. (с использованием компьютера)

Ход работы.

1. Создайте в GeoGebra динамическую модель треугольника, зависящую от трех параметров а, b и с – длин его сторон. Установите области изменений параметров так, чтобы выполнялось неравенство

a b c < a + b.

Выведите на экран текущее значение большего угла треугольника ().

2. Выберите и зафиксируйте значения параметров a и b. Включите опцию запись в таблице исследуемых величин: a2 + b2; c2. Изменяйте значение с.

3. Скопируйте таблицу данных эксперимента (см. рис. 117) в файл Excel.

4. Повторите эксперимент несколько раз для различных сочетаний значений a и b.

5. Используйте собранные данные, чтобы сделать выводы, отвечающие на поставленные вопросы.

Приведенные примеры показывают, что задания на проведения экспериментов в лабораторных работах этого вида существенно не различаются. Главным отличием является форма организации работ. Поскольку в большинстве случаев объект математического исследования – класс
эквивалентности, то для выдвижения гипотез о его свойствах необходимы массовые данные. В условиях ограниченного времени (урок или часть урока) получить достаточное количества данных, экспериментируя с вещественными моделями (моделями единичных представителей этого класса) можно лишь путем организации коллективной работы. Виртуальные модели математических объектов за счет задания и варьирования динамики, позволяют формировать репрезентативные выборки представителей изучаемого класса достаточно большого объема, и оперативно формировать массивы экспериментальных данных. Экспериментирование с такими моделями занимает не более 1–3 минут. Основное время тратится на создание адекватной модели. Все это позволяет использовать индивидуальную форму организации компьютерной лабораторной работы.

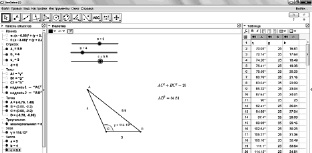
Рис. 117. Решение примера 3

Различия иллюстративных лабораторных работ, проводимых с компьютером и без него, не ограничиваются различием форм организации работы учащихся. Здесь выбор средств создания модели объекта изучения для проведения контрольных экспериментов имеет принципиальное значение. Покажем это на конкретных примерах.

Пример 4. Лабораторно-иллюстративная работа на тему «Равносильные преобразования».

Цель: Найти практическое подтверждение правилу:

«Для того, чтобы упростить уравнение или неравенство можно из обеих его частей вычесть одно и тоже число. Множество корней уравнения/неравенства при этом не изменится, то есть

A(x) + c = (<, >)B(x) + c A(x) = (<, >)B(x)».

Вариант 1 (без использования компьютера)

Постановка задачи: Решение уравнений и неравенств в большинстве случаев требует их сведения к простейшему стандартному или каноническому виду, т.е. к такому виду, для которого установлено правило описания множества корней (решений). Для того, чтобы множество корней (решений) не исказилось в процессе этой работы необходимо пользоваться правилами равносильных преобразований. Истинность этих правил должна быть подтверждена доказательством, или хотя бы проиллюстрирована аналогичными правилами практических действий на моделях уравнений и неравенств. Поскольку слева и справа от знака равенства (неравенства) находятся некоторые переменные, выраженные количественно, то логично интерпретировать процесс решения уравнений (неравенств) как поиск объектов, массы которых находятся в указанном отношении, методом взвешивания на весах.

Ход работы.

1. Поставьте на чашки весов два любых предмета так, чтобы весы находились в равновесии (рис. 118). Один предмет назовите А, другой В. Поставьте на обе чашки весов по гире одинаковой массы (назовите ее с). Запишите, изменилось ли и как показание весов.

2. Повторите эксперимент, подобрав предметы так, чтобы масса А была меньше массы В. Запишите изменение показания весов.

3. Повторите эксперимент для А > B. Запишите результат.

Вариант 2 (с использованием компьютера)

Постановка задачи: Решение уравнений и неравенств в большинстве случаев требует их сведения к простейшему стандартному или каноническому виду, т.е. к такому, для которого установлено правило описания множества корней (решений). Для того, чтобы множество корней (решений) не исказилось в процессе этой работы необходимо пользоваться правилами равносильных преобразований. Истинность этих правил должна быть подтверждена доказательством, или хотя бы подтверждена достаточно большим количеством примеров. Для испытания работы правила для различных значений c проведем компьютерный эксперимент.

Ход работы.

1. Задайте в GeoGebra изображения двух параметром:

1) параметра c, принимающего значения из произвольно выбранного вами промежутка с шагом 0,05;

2) параметра x, принимающего значения с шагом 0,01 из области допустимых значений уравнения 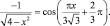(1):

(1)

2. Создайте в панели объектов GeoGebra зависящие от значений параметра x вычислимые переменные: 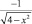и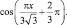

3. Создайте в панели объектов GeoGebra зависящие от значений параметров x и c вычислимые переменные: 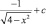и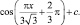

4. Используйте эти четыре переменных для создания динамических текстов (см. рис. 119).

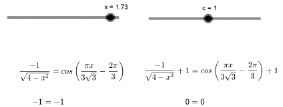
Рис. 119. Решение примера 4

5. Зафиксируйте произвольно значение с. Найдите корни представленных уравнений, перебором значение переменной x. Запишите результат.

6. Измените значение с. Снова найдите перебором корни нового уравнения. Опыт повторите несколько раз. Сделайте вывод о существовании или отсутствии значений c, нарушающих равносильность уравнений.

Представленные примеры показывают, что в лабораторные работы иллюстративного плана, проводимые с компьютером и без него, не всегда взаимозаменяемы. Они предоставляют разные с идейной точки зрения способы верификации математических утверждений. В связи с этим их лучше использовать в сочетании. Это позволит добиться более высокого уровня понимания материала учащимися, обладающими различными стилями мышления.

Заметим, что в лабораторных работах иллюстративного характера сочетание заданий на проведение компьютерных экспериментов с экспериментированием над вещественными моделями является хоть и желательным, но не обязательным. Обязательным оно является при проведении работ другого типа – лабораторно-практического. Здесь компьютерные эксперименты выполняются вспомогательную роль, позволяя получать дополнительные сведения о свойствах объектов исследования. Натурные эксперименты служат для проверки практической реализуемости предложенных решений проблемы и оценки условий их эффективности. Покажем это на конкретном примере.

Пример 5. Лабораторная работа по теме «Площадь треугольника».

Цель: освоение особенностей практического применения метода вспомогательных площадей.

Постановка задачи: В сельской местности расположено три небольших населенных пункта А, В и С. Каждые два поселка соединены автомобильной дорогой. В связи с планами организации движения общественного транспорта по этим дорогам, необходимо определить места строительства автобусных остановок. Они должны быть расположены на каждой дороге так, чтобы расстояние от населенного пункта, через который дорога не проходит, было наименьшим. Разработайте типовой план, считая:

– не существенными размеры населенных пунктов;

– расстояние между каждой парой из них известным с точностью до 100 м.

Ход работы.

1. Решите задачу аналитически, используя метод вспомогательных площадей.

2. Создайте компьютерную модель ситуации (см. рис. 120). Используйте ее для построения геометрических мест расположения автобусных остановок, определенных погрешностями измерения.

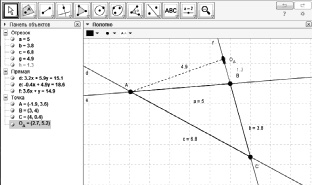
Рис. 120. Решение к примеру 5

3. Найдите в Интернет правила арифметических действий с приближенными значениями. Пользуясь ими, объясните величину результирующей погрешности.

4. Найдите на карте своего района три населенных пункта, соответствующих условию задачи. Пользуясь расчетами, укажите возможные места расположения автобусных остановок с указанием погрешности измерения.

Последним из названных нами видов являются лабораторно-обобщающие работы. Для достижения обобщений предпочтительнее виртуальные модели объектов исследования и серии модифицирующих компьютерных экспериментов. Это позволит избежать влияния неточности практических действий, снизит трудоемкость работ по получению и обследованию множества модификаций объекта исследования. Продемонстрируем это на конкретном примере.

Пример 6. Лабораторная работа на тему «Графический метод решения уравнений и неравенств».

Цель: обобщить графический метод решения уравнений на случай неравенств.

Постановка задачи: Известен графический метод решения уравнений вида:

f(x) = g(x). (2)

Этапы применения метода:

1) Заменить уравнение (2) равносильной ему системой

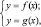
где y = f(x) и y = g(x) – функции.

2) Построить графики функций на их общей области определения.

3) Найти абсциссы точек пересечения графиков функций.

4) Проверить подстановкой, являются ли они приближенным/точными значениями корней уравнения или являются посторонними корнями.

Если y = f(x) и y = g(x) являются функциями известного вида, то для решения уравнения (2) могут быть использованы эскизы их графиков, построенные в ручную. Если нет, то для построения графиков привлекаются компьютерные средства.

Логично предположить, что возможности компьютера могут быть использованы не только для этих целей, но и для решения вопроса о том, как изменится план действий, если применять графический метод к решению неравенств f(x) g(x). Вам предстоит, опираясь на это предположение, обобщить графический метод на случай неравенств.

Ход работы.

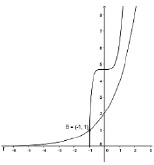
1. Используя возможности программы GeoGebra, решите графическим методом какое-либо уравнение, например: 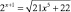(см. рис. 121).

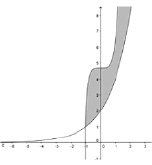
2. Измените графическую модель задачи так, чтобы она могла быть использована для решения аналогичного неравенства 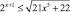(рис. 122).

3. Проанализируйте полученное изображение, сделайте вывод об изменениях, которые нужно внести в описание графического метода для его распространения на случай неравенств.

Резюмируя представленный в данном параграфе обзор видов лабораторных работ, считаем важным обратить внимание читателей еще раз на тот факт, что лабораторный практикум по математике ни в коем случае не может состоять их одних заданий на проведение компьютерных экспериментов. Каждый раз нужно рассматривать все методические возможности математических задач, принимая решение с учетом целевого назначения лабораторной работы, особенностей объекта исследования, возможностей имеющихся в распоряжении средств моделирования и экспериментирования с моделями.

Рис. 121 Рис. 122