
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ
Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,
3.4. Организация исследовательской работы учащихся с учетом идей экспериментальной математики
Данный параграф посвящен описанию опыта включения учащихся основной и старшей школы в деятельность по подготовке исследовательских работ с применением GeoGebra. Таких работ за годы реализации проекта MITE под руководством учителей – экспериментаторов накопилось уже достаточно большое количество для обобщения накопленного опыта.
|
Тема работы |
ФИО исполнителя |
Лучший конкурсный |
|
Исследование положения ортоцентров треугольников, вписанных в гиперболу |
Пятин Илья (10 класс), науч. руководитель – Паршева В.В. |
2 место в международном конкурсе «Математика и проектирование», 2013 г. |
|
Сангаку – математические секреты японских храмов |
Попова Анна (10 класс), науч. руководитель – Петрова М.В. |
2 место в международном конкурсе «Математика и проектирование», 2014 г. |
|
Геометрия дельтоида |
Евсикова Дарья (10 класс), науч. руководитель – Белорукова М.В. |
1 место на городской научной конференции «Юность Архангельска»; 2014 г.; 2 место на областной конференции «Юность Поморья», 2014 г.; 3 место в международном конкурсе «Математика и проектирование», 2014 г. |
|
Свойства касательной к гиперболе |
Максимовский Константин (9 класс), науч. руководитель – Паршева В.В. |
2 место в международном конкурсе «Математика и проектирование», 2015 г. |
|
Замечательные точки и линии в треугольнике: золотой ключ Леонарда Эйлера |
Плесов Илья (9 класс), науч. руководитель – Паршева В.В. |
3 место в международном конкурсе «Математика и проектирование», 2015 г. |
|
Такая простая и сложная кардиоида |
Евсикова Дарья (11 класс), науч. руководитель – Белорукова М.В. |
3 место на городской научной конференции «Юность Архангельска», 2015 г.; 1 место на областной конференции «Юность Поморья», 2015 г.; 1 место в международном конкурсе «Математика и проектирование», 2015 г. |
Опишем опыт работы наиболее успешных научных руководителей на конкретных примерах постановки ими исследовательских задач в сфере экспериментальной математики и организации деятельности учащихся по подготовке исследовательских работ.
3.4.1. Постановка задач на исследование некоторых свойств гиперболы учащимися 9–10 классов
Кривые второго порядки с древних времен привлекали к себе внимание ученых. Замечательные геометрические объекты – кривые линии привлекают внимание не только изяществом своей формы, но и многими удивительными свойствами. В школьном курсе математики в качестве кривых второго порядка рассматриваются графики квадратичной функции и обратной пропорциональности – парабола и гипербола. Они изучаются на уроках алгебры как графики элементарных функций, и поэтому основное внимание уделяется их аналитическим свойствам. Изучение геометрических свойств этих кривых ограничивается лишь двумя вопросами:
– рассмотрением случаев их взаимного расположения с прямыми, так как эти случаи часто используется при графическом решении уравнений, построении графиков этих функций;
– выделением осей и точек симметрии в качестве геометрической интерпретации свойств четности и нечетности функций.
Парабола и гипербола как геометрические объекты рассматриваются лишь в классах с углубленным изучением математики. Здесь они трактуются как геометрические места точек, обладающих определенными свойствами. Учащиеся знакомятся с каноническими уравнениями этих кривых, с такими понятиями как фокус и директриса кривых. Изучают оптические свойства, необходимые для курса физики [3, с. 18–28]. В то же время парабола и гипербола имеют и другие интересные геометрические свойства, которые остаются за страницами школьных учебников.
Применение GeoGebra позволяет включить учащихся в деятельность комплексного изучения кривых второго порядка, поиска большого количества их геометрических свойств, оценки значимости знания этих свойств для решения разного типа задач, прежде всего задач на построение [137].
Рассмотрим исследование некоторых свойств гиперболы, которое было проведено учащимися 9–10 класса еще до изучения производной.
Постановка задачи переноса известных свойств окружности на гиперболу. Для подведения учащихся к постановке задачи исследования было организовано повторение известных свойств гиперболы:
– Гипербола – это график функции, называемой обратной пропорциональностью.
– Гиперболу можно задать уравнением 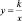 , k 0.
, k 0.
– Гипербола состоит из двух бесконечных кривых, разделенных осями координат.
– Гипербола располагается в I и III координатных углах, если k > 0, и во II и IV координатных углах, если k < 0.
– График имеет две асимптоты: х = 0 и у = 0.
– График имеет центр симметрии – начало координат О (0;0).
– График имеет две взаимно перпендикулярных оси симметрии: у = x и у = –x.
Актуализация знаний учащихся об уравнении, задающем гиперболу, позволяет ввести по отношению к ней, а также по отношению к окружности термин «кривая второго порядка» – линия задаваемая уравнением второй степени: ax2 + by2 + cx + dy + k = 0. Наличие обобщающего термина ставит перед учащимися задачу переноса известных свойств окружности на гиперболу.
В частности, ученики, на уроках геометрии знакомясь с тем фактом, что в окружность можно вписать треугольник, могут задаться вопросами: Можно ли в другие кривые второго порядка вписать треугольник? Какими свойствами обладает такой треугольник?
Искать ответы на эти вопросы помогает компьютерный эксперимент, проведенный в GeoGebra. Ученикам предлагается с помощью инструментов программы построить динамический чертеж гиперболы 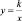 с параметрически заданным значением k. На гиперболе отметить произвольно три точки – это вершины треугольника, вписанного в гиперболу.
с параметрически заданным значением k. На гиперболе отметить произвольно три точки – это вершины треугольника, вписанного в гиперболу.
С помощью инструмента Перпендикулярная прямая  найти ортоцентр этого треугольника. Варьируя значения параметра k и положения вершин треугольника на гиперболе, учащиеся легко приходят к выдвижению гипотезы: Ортоцентр треугольника, вписанного в гиперболу, принадлежит этой же гиперболе (рис. 123).
найти ортоцентр этого треугольника. Варьируя значения параметра k и положения вершин треугольника на гиперболе, учащиеся легко приходят к выдвижению гипотезы: Ортоцентр треугольника, вписанного в гиперболу, принадлежит этой же гиперболе (рис. 123).
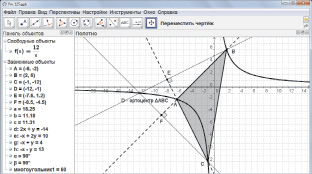
Рис. 123
После этого ученикам может быть предложено доказать справедливость гипотезы, для чего учащимся потребуются знания формул прямой, заданной двумя точками, уравнения прямой, перпендикулярной данной и проходящей через заданную точку, умение находить координаты точки пересечения двух прямых и умение определять принадлежность точки кривой.
Постановка задачи изучения геометрического способа задания гиперболы. В GeoGebra есть целый набор инструментов, позволяющих строить окружность из геометрических соображений. Предусмотрен также инструмент и для построения гиперболы. Особенностью этого инструмента является то, что он не снабжен указаниями по его использованию. Пиктограмма  явно подсказывает, что гипербола задается тремя точками, лишь одна из которых является точкой самой гиперболы. Исследовательская задача, решаемая учащимися средствами GeoGebra, может быть связана с выяснением смысла остальных двух точек и их значения для задания гиперболы.
явно подсказывает, что гипербола задается тремя точками, лишь одна из которых является точкой самой гиперболы. Исследовательская задача, решаемая учащимися средствами GeoGebra, может быть связана с выяснением смысла остальных двух точек и их значения для задания гиперболы.
Постановка задачи на исследование свойств касательной к гиперболе. Данная задача возникает вновь из соображений возможности переноса известных свойств окружности в новую ситуацию. В данном случае внимание учащихся обращается на случаи взаимного расположения окружности и прямой.
Экспериментируя с моделями гиперболы и прямой в GeoGebra, ученики убеждаются в том, что прямая и гипербола (также как прямая и окружность) могут иметь не более двух общих точек. Это позволяет ввести понятие касательная к гиперболе. Экспериментируя с изменением положения точки касания, учащиеся могут обнаружить интересные свойства касательной к гиперболе:
1. Касательная, проведенная в любой точке гиперболы, образует с осями координат треугольник постоянной площади, не зависящей от точки касания, и эта площадь равна 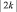 (рис. 124).
(рис. 124).
2. Отрезок любой касательной к гиперболе, заключенный между осями координат, делится точкой касания пополам.
3. Касательная, проведенная к гиперболе в точке (х0; k/х0) пересекает ось абсцисс в точке (2х0; 0) и ось ординат в точке (0; 2k/х0).
4. Точка касания является центром окружности, описанной около треугольника, отсекаемого касательной от осей координат (рис. 125).
К доказательству справедливости выдвинутых гипотез учащиеся смогут вернуться позже (после изучения понятия производной и уравнения касательной к графику функции).
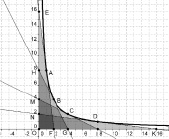
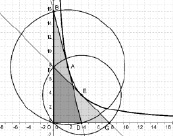
Рис. 125
Отсутствие знаний об уравнении касательной ставит перед учащимися интересную исследовательскую задачу – придумать способы построения касательной к графику y = k/x в любой точке графика без нахождения уравнения касательной. Приведем несколько способов, предложенных учащимися.
Способ первый. Точка касания является центром окружности, описанной около треугольника, отсекаемого касательной от координатных осей, а радиусом является отрезок с началом в данной точке и концом в точке (0; 0). Построив такую окружность, мы получаем вершины треугольника, лежащие на координатных осях. Прямая, проходящая через них – искомая касательная (см. рис. 125).
Способ второй. Опустить перпендикуляр на ось Ох из данной точки касания. Полученный перпендикуляр будет являться средней линией треугольника, отсекаемого касательной от координатных осей. По найденной середине катета строят вершину треугольника и через нее и точку касания проводят искомую касательную (рис. 126).
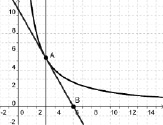
Рис. 126
Способ третий. Площадь треугольника, который отсекается касательной, равна 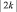 . Значит, произведение катетов такого треугольника равна
. Значит, произведение катетов такого треугольника равна 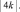 Для гиперболы
Для гиперболы 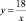 произведение катетов равно 72. Если один катет равен 12, то другой равен 6. Отметим на оси Ох точку (6; 0), а на оси Оу – точку (0; 12).Через точки (6; 0) и (0; 12) проведем прямую. Это и будет касательная. Выбираем другие значения: один катет 18, другой 4. Через точки (18; 0) и (0; 4) проводим вторую касательную. Ученики приходят к выводу, что задача имеет множество решений (рис. 127).
произведение катетов равно 72. Если один катет равен 12, то другой равен 6. Отметим на оси Ох точку (6; 0), а на оси Оу – точку (0; 12).Через точки (6; 0) и (0; 12) проведем прямую. Это и будет касательная. Выбираем другие значения: один катет 18, другой 4. Через точки (18; 0) и (0; 4) проводим вторую касательную. Ученики приходят к выводу, что задача имеет множество решений (рис. 127).
Так мы приходим к еще одному интересному свойству гиперболы: гипербола является огибающей прямых, отсекающих от прямого угла треугольники одной площади S, т.е. гипербола касается всех таких прямых. Ученикам предлагается найти способ построения гиперболы, используя понятие огибающей.
Найденные учащимися способы построения касательных с опорой на «открытые» ее свойства могут быть использованы для поиска уравнений касательных.
Все перечисленные исследовательские задачи составляют одну «цепочку», поэтому целесообразно их ставить и реализовывать этап их компьютерного решения на одном установочном занятии (продолжительность 1,5 академических часа). Форма организации работы учащихся
на таком занятии – групповая. Каждая группа решает свою задачу в отведенное ей время. Затем подготавливается делает отчет о выполненной работе. После отчета каждой группы подводится общий итог работы: «Какое открытие было сделано на занятии?»
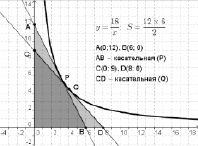
Рис. 127
Практика организации такой работы показывает, что микроисследования, проведенные на занятиях, часто становятся для учащихся стартом к выполнению ими проектно-исследовательских работ во внеурочное время.
Так, например, данная «цепочка» задач послужила отправной точкой для выполнения двух работ: «Свойства касательной к гиперболе» и «Исследование положения ортоцентров треугольников, вписанных в гиперболу».
3.4.2. Применение GeoGebra в постановке и решении задач Сангаку
Сангаку – это цветные деревянные дощечки, выставляемые в синтоистских святилищах, а иногда и в буддийских храмах в Японии, изображающие математические задачи (см. рис. 128 и 129).
Искусство Сангаку называют Японской храмовой геометрией. Знакомство учащихся с Сангаку на научно-популярных занятиях установочного характера приводит учащихся к постановке целой серии исследовательских вопросов: Зачем и для кого в храмах выставляли эти таблички? Связаны ли представленные на них геометрические задачи с религиозными учениями? Если связаны, то как? Кто составлял эти задачи? В чем особенность постановки и решения задач Сангаку? Все ли они имеют решение? Если да, то какое?


Рис. 128 Рис. 129
Поиск ответов на эти вопросы может стать предметом не только культурологических, но и математических исследований учащихся. Исследовательская работа по математике начинается с поиска информации о задачах Сангаку в сети Интернет. Результатом этой работы является создание коллекции задач, заимствованных из российских и зарубежных источников с решениями и без них. Анализ этой коллекции приводит учащихся к выводу, что словестная постановка задач Сангаку чаще всего является неполной, порой даже вовсе отсутствует. Это ставит перед ними проблему поиска значимых для решения задачи данных. Решение этой проблемы может быть осуществлено путем воссоздания чертежа классическими конструктивными инструментами (циркулем и линейкой) или средствами интерактивной математической среды (например, GeoGebra).
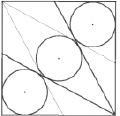
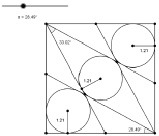
Представим работу ученика над одной из задач Сангаку на следующем примере: «Дан квадрат со стороной 1. Найдите радиусы кругов на рис. 130, если известно, что они равны».
Поверхностный анализ конфигурации, представленной на этом рисунке, приводит к предположению о равенстве углов, на которые разделен угол квадрата лучами, исходящими из его вершины, т. е. гипотезы о том, что лучи, исходящие из вершины квадрата, проведены под углом 30° к его сторонам.
Для проверки этой гипотезы учащийся строит динамический чертеж, выбирая в качестве параметра угол, из которого проведены лучи, и проводит компьютерный эксперимент. Результаты этого эксперимента представлены на рис. 131. Они свидетельствуют о сомнительности первой гипотезы (не позволяя, однако полностью от нее отказаться).
Это мотивирует ученика к поиску аналитического решения, которое также сопряжено с некоторыми трудностями. Для того чтобы продемонстрировать их, представим решение, предложенное иным исследователем.
Пусть прямая, исходящая из вершины квадрата под углом ? (острым), отсекает от квадрата прямоугольный треугольник, в который может быт вписан круг с радиусом r. Тогда получаем уравнение (1):
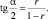 (1)
(1)
Так как из одной вершины квадрата проведены две прямые под углом ? к смежным сторонам квадрата, то при смежных сторонах квадрата образуются равные прямоугольные треугольники. Также получаем ромб, острый угол которого равен 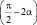 . Так как в ромб вписан круг радиуса r, то получаем уравнение (2):
. Так как в ромб вписан круг радиуса r, то получаем уравнение (2):
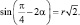 (2)
(2)
Составим из уравнений (1) и (2) систему для получения уравнения относительно искомой переменной r.
Используя тождества
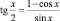 и
и 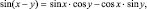
приведем тригонометрические функции к одному аргументу:
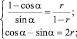
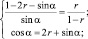
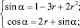
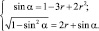 (3)
(3)
Из (3) окончательно получаем уравнение относительно r:
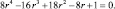 (4)
(4)
Подбором легко находится один из корней этого уравнения r = 0,5, который, очевидно, не удовлетворяет условию исходной задачи. Однако его обнаружение позволяет свести уравнение (4) к уравнению третьей степени:
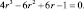 (5)
(5)
Других рациональных корней обнаружить не удалось. Используем GeoGebra для нахождения приближенного значения корня полученного уравнения:
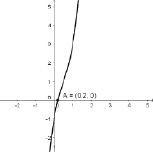
Рис. 132
Полученный приближенный результат вполне согласуется с результатами компьютерного эксперимента, однако не позволяет говорить о завершенности работы над задачей. Данная ситуация ставит перед
учащимся задачу сбора данных о методах нахождения корней многочленов с целыми коэффициентами и их самостоятельного освоения. Числовое выражение для искомого корня может быть получено, например, с использованием формулы Кардано [7].
С помощью подстановки: r = y + 0,5 приведем уравнение к каноническому виду:
y3 + 0,75y + 0,25= 0. (9)
Данное уравнение имеет один действительный корень, так как 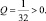 Он имеет вид:
Он имеет вид:
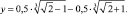
Тогда
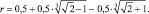
3.4.3. Моделирование кардиоиды в GeoGebra
Кардиоида, улитка Паскаля, астроида, нефроида – эти линии были известны ещё древним математикам, и многочисленные проблемы механики, астрономии, геодезии, оптики, возникшие в XVII–XVIII веках, стимулировали глубокий интерес к исследованию свойств этих линий. Эти проблемы привели также к открытию новых линий, возникших при рассмотрении чисто практических вопросов, а также в теоретических исследованиях. Крупнейшие математики эпохи с необыкновенным рвением занимались изучением кривых, открывая всё новые и новые их виды и свойства. Но не только практические потребности века поддерживали постоянный и глубокий интерес к исследованию кривых, но и та «радость созерцания формы», которая, по словам Клейна, характеризует истинного геометра [78].
Итак, рассмотрим задачу: Пусть окружность катится с внешней стороны по другой окружности того же радиуса. Нарисуйте кривую, которую описывает при этом точка, закреплённая: на окружности; на радиусе внутри катящейся окружности; на продолжении радиуса катящейся окружности [84].
Для решения используем интерактивную геометрическую среду GeoGebra. Построив модель катящейся окружности по другой окружности, получаем следующий результат: точка B? катящейся окружности описывает кривую, изображённую на рис. 133, а. Полученную кривую из-за схожести своих очертаний со стилизованным изображением сердца (от греч. «кардиоида» – сердце) называли кардиоидой.
Изменив в модели положение точка B?, получим следующее: Если точку B? брать не на катящейся окружности, а на радиусе или его продолжении, то получим кривые, изображённые на рис. 133, б и в. Первую из них называли укороченной, а вторую – удлинённой кардиоидой.
Все три вида кривых получили название улиток Паскаля. Такое название им дал французский математик Жюль Роберваль (1602–1675) по имени их открывателя Этьена Паскаля – отца Блеза Паскаля.
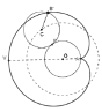
а б в
Рис. 133. Кардиоиды
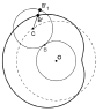
Рассмотрим случай, когда неподвижная окружность и катящаяся по ней имеют произвольные радиусы R и r. Эти окружности могут касаться друг друга внешним или внутренним образом. В зависимости от отношения радиусов окружностей R : r точка, лежащая на подвижной окружности, описывает различные кривые, которые называются в первом случае эпициклоидами (см. рис. 134), а во втором – гипоциклоидами (см. рис. 135).
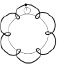
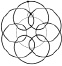
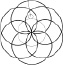
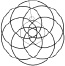
Рис. 134. Эпициклоиды, R : r = 6
Если точка находится не на катящейся окружности, а лежит вне или внутри ее, то кривая называется удлиненной или укороченной эпи-, гипоциклоидой.
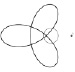
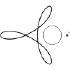
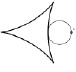
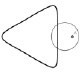
Рис. 135. Гипоциклоиды, R : r = 3
Построенную модель и её модификации можно назвать кинематическими моделями. Известно, что существуют и другие модели кардиоиды. Например, алгебраическая модель – уравнение кардиоиды в полярной системе координат [3]:
? = 2r(1 ± cos?).
Чем отличаются кардиоиды, построенные по этим двум уравнениям? Существуют ли другие уравнения?
К сожалению, ИГС GeoGebra не строит кривых, заданных в полярной системе координат. Вопрос решает уравнение кардиоиды, заданное параметрически, и возможности среды строить траектории движения точки с помощью инструментов Оставлять след  и Локус
и Локус  .
.
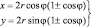 – параметрические уравнения кардиоиды.
– параметрические уравнения кардиоиды.
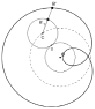
Теперь в ИГС GeoGebra можно задать координаты точки М с помощью полученных формул, а саму кривую построить с помощью инструментов Оставлять след или Локус. Полученные кардиоиды отличаются друг от друга только началом построения: из вершины или каспа (см. рис. 136).
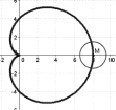
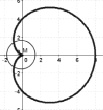
Рис. 136
Исходя из определения кардиоиды, данная кривая может иметь различные положения на плоскости. На рис. 136 касп располагается слева, а вершина – справа. Возникает вопрос: как будут выглядеть уравнения кардиоиды при других её расположениях? Рассмотрим следующие расположения кардиоиды:
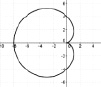
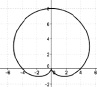
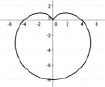
a б в
Рис. 137
Начнём компьютерный эксперимент с изменения знака. Пусть ? = –2r(cos ? ± 1). Тогда параметрические уравнения примут вид:
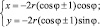
Получим кардиоиду, изображённую на рис. 137,а.
Вывод: изменение знака симметрично отображает кардиоиду относительно вертикальной оси, и уравнение кардиоиды имеет вид
? = ±2r(cos ? ± 1).
Продолжим экспериментировать с уравнением кардиоиды. Заменим функцию cos ? на sin ?: ? = ±2r(sin ? ± 1). Получим следующие параметрические уравнения:
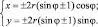
Данным уравнениям соответствует кардиоида, изображённая на рис. 137, б и в.
Вывод: Если в уравнении кардиоиды заменить функцию cos ? на sin ?, то кардиоида поворачивается на 90° по или против часовой стрелки. Объяснить это можно с помощью формул приведения: cos (? ± 90°) = ±sin ?.
Что может получиться, если к углу ? прибавить произвольный угол ?? Компьютерный эксперимент показывает, что в этом случае кардиоида поворачивается на угол ?.
Таким образом, уравнение кардиоиды в полярной системе координат может принимать вид:
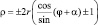 [24].
[24].
Поиграем в ИГС GeoGebra с параметром 2r. Раскроем скобки в уравнении кардиоиды ? = 2r(cos ? ± 1) = 2rcos ? ± 2r и заменим слагаемое 2r на параметр a: ? = 2rcos ? ± a. Построим кривую, заданную полученным уравнением в ИГС GeoGebra. Координаты точки М, лежащей на этой кривой будут задаваться уравнениями:
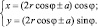
Проведём компьютерный эксперимент: будем менять численные значения параметра a и наблюдать, как при этом меняется форма кривой.
В ходе компьютерного исследования, мы получили следующие результаты:
1) если a < 2r, то полученная кривая является удлинённой кардиоидой (см. рис. 138, а);
2) если a = 2r – кардиоидой (см. рис. 138, б);
3) если a > 2r – укороченной кардиоидой (см. рис. 138, в).

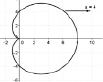
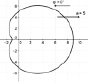
а б в
Рис. 138
Поэкспериментируем с уравнением ? = 2rcos ? ± a так же, как и с уравнением кардиоиды.
В ходе этого эксперимента получили различные расположения улитки Паскаля на плоскости и обобщённое уравнение:
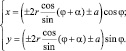
Статья С.В. Ларина «Геометрическое моделирование действий с комплексными числами средствами GeoGebra» [65], подсказала идею ещё одного способа моделирования кардиоиды: построим в среде многочлен второй степени от комплексного переменного, модуль которого равен 1:
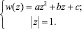
Эксперимент, проведённый в среде GeoGebra, показывает, что многочлен w(z) описывает кривую, похожую на улитку Паскаля.
Попробуем доказать, что это действительно улитка Паскаля.
Пусть z = x + iy, тогда z2 = x2 – y2 + 2ixy.
Перейдем к полярной системе координат: x = rcos ?, y = rsin ?.
Так как 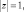 r = 1,
r = 1,
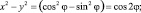
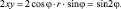
Выполнив преобразования, получим:
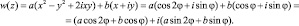
Получили уравнение, похожее на параметрическое уравнение кардиоиды:
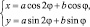
правда, с комплексными коэффициентами a и b. Дальнейшие преобразования в общем виде являются сложными, так как требуется введение вспомогательного аргумента угла. Если же данную задачу решить для конкретного многочлена, то гипотеза подтверждается.
Решение следующих задач [24] даёт ещё несколько способов построения кардиоиды и формулировки её определения.
Задача 1. Что представляет собой множество оснований перпендикуляров, опущенных из точки данной окружности на всевозможные касательные к ней?
Задача 2. Что представляет собой множество всех точек, симметричных определённой точке данной окружности относительно всевозможных касательных к этой окружности?
Задача 3. Если на каждой прямой l, проходящей через точку A данной окружности ? радиуса r, отложить от точки Q пересечения l и ? (A ? Q) отрезок QM длины 2r, то множество всех полученных таким образом точек M будет кардиоидой.
Итак, моделирование в ИГС позволило наглядно продемонстрировать различные определения кардиоиды, рассмотреть способы её построения и всевозможные расположения кардиоиды в системе координат, исследовать многочлены второй степени от комплексного переменного z,  .
.