Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭКСПЕРИМЕНТАЛЬНАЯ МАТЕМАТИКА В ШКОЛЕ. ИССЛЕДОВАТЕЛЬСКОЕ ОБУЧЕНИЕ

Шабанова М. В., Овчинникова Р. П., Ястребов А. В., Павлова М. А., Томилова А. Е., Форкунова Л. В., Удовенко Л. Н., Новоселова Н. Н., Фомина Н. И., Артемьева М. В., Ширикова Т. С., Безумова О. Л., Котова С. Н., Паршева В. В., Патронова Н. Н., Чиркова Л. Н., Тепляков В. В.,

3.5. Технология разработки и проведения исследовательского урока

Я хотел бы, чтобы изобретатели дали историю путей, по которым они дошли до своих открытий. В тех случаях, когда они вовсе не сообщают этого, нужно попробовать отгадать эти пути.

Готфрид Лейбниц

Мозг хорошо устроенный стоит больше, чем мозг хорошо наполненный.

Мишель Монтень

3.5.1. Введение. Основные понятия

В настоящее время в школьном образовании происходит переоценка роли и места исследовательской деятельности в процессе обучения учащихся, что обусловлено требованиями модернизации образования и Федерального государственного стандарта основного общего. В соответствии с ФГОС ООО совершенствование форм и методов учебной работы, повышение эффективности учебно-воспитательного процесса, главным образом, нацелено на формирование у учащихся навыков и способностей к определенным видам деятельности, обладающим свойством универсальности и могущим быть реализованными на различном содержании и перенесенными в будущую учебную и профессиональную деятельность. К таким видам деятельности относится исследовательская деятельность.

Система современного общего образования, опираясь на личностно-ориентированный подход в обучении, ориентируется на когнитивные возможности и особенности учащихся при освоении ими определенного содержания. Это выражается в отказе от авторитарных методов обучения, в построении методики, опирающейся на психологические закономерности процесса познания, в предоставлении учащимся достаточной степени свободы в выборе способов овладения знаниями, в опоре на личностный (жизненный и учебный) опыт учащихся при осуществлении обучения. Реализация личностно-ориентированного подхода требует выбора таких методов обучения, которые бы ставили ученика в активную позицию, создавали условия для его равноправного участия в планировании, организации, проведении и корректировке образовательного процесса. К таким методам, в частности, относится исследовательский метод. Исследовательский подход в обучении способствует:

– раскрытию наиболее существенных сторон, характеристик изучаемого понятия, их взаимосвязей с другими понятиями с одновременным установлением ценности нового знания для учащихся;

– формированию научного мышления, через аккумулирование, компиляцию и обобщение приобретаемых знаний;

– развитию творческой активности учащихся в процессе учебного познания и созданию условий для научно-образовательной, поисково-творческой деятельности;

– активному использованию различных форм учебной работы в сочетании с разными организационных формами обучения;

– стимулированию готовности и способности проявлять учащимися познавательную и деятельностную инициативу в создаваемых условиях гармоничного соотнесения научно-образовательной, поисково-творческой деятельности в условиях учебной и внеучебной работы по изучению основных понятий предметной области.

В связи с этим важным является целенаправленное стимулирование познавательной активности у обучаемых с целью формирования у них ряда определенных исследовательских умений непосредственно на уроке и вне его. Формирование исследовательских умений в условиях организации образовательного процесса осуществлялось нами через организацию учебно-исследовательской деятельности.

Под учебно-исследовательской деятельностью понимается активная, целенаправленная, недетерминированная учебно-познавательная
деятельность, которая направлена на открытие нового для учащегося знания об объекте исследования, способе или средстве деятельности и характеризуется наивысшей степенью самостоятельности и творческим отношением к процессу исследования [85].

Урок, на котором целенаправленно организуется знакомство учащихся с методикой исследовательской деятельности, называют уроком-исследованием.

Основными отличиями урока-исследования от исследовательской деятельности являются временные рамки и конечный результат. Исследовательская деятельность почти не ограничена во времени и результат её неизвестен. Урок-исследование ограничен – это, обычно, один или два спаренных урока. На таком уроке перед учащимися ставится исследовательское задание (задача), решение которого в науке известно, но для учащихся оно является субъективно новым.

В соответствии с основными структурными элементами исследовательской деятельности и требованиями к современному уроку, можно выделить следующие этапы урока-исследования:

1. Актуализация знаний.

2. Этап мотивации и постановки проблемы исследования.

3. Сбор фактического материала.

4. Систематизация и анализ полученного материала.

5. Выдвижение гипотезы.

6. Проверка гипотезы.

7. Доказательство истинности гипотезы.

8. Вывод по результатам исследовательской работы, о применении полученных знаний.

9. Подведение итогов урока.

10. Домашнее задание.

На уроке, как правило, лучше, если исследовательские задания представляют собой небольшие исследовательские задачи, требующее прохождения через все или большинство этапов процесса исследования.

Урок, на котором учащиеся отрабатывают отдельные учебно-исследовательские умения, называют уроком с элементами исследования.

3.5.2. Цели и задачи урока-исследования

Целями урока-исследования являются:

– формирование знаний об исследуемых объектах и способах оперирования ими;

– формирование знаний о структуре и компонентах исследовательской деятельности,

– развитие исследовательских умений,

– развитие универсальных учебных действий.

Под учебно-исследовательскими умениями понимают умения полностью или частично реализовывать этапы исследовательской деятельности на различном предметном содержании.

Н.Л. Стефанова подразделяет исследовательские умения на:

– обобщенные (общие) исследовательские умения, инвариантные относительно различного содержания,

– специфические, используемые в отдельных дисциплинах и предметных областях и

– инструментальные умения (умения работы с оборудованием).

Конкретизируем список исследовательских умений, наиболее часто используемых учащимися в процессе изучения учебного математического материала, относящихся к этим видам на основе анализа научных исследований в данной области [26, 36, 85, 88].

Обобщенные умения:

– работать с учебной, справочной и научно-популярной математической литературой, поисковыми системами;

– осуществлять основные логические операции;

– ставить вопросы к данным;

– формулировать учебную проблему в общем виде и выделять подпроблему;

– искать всевозможные направления поиска решения проблемы и выделять то, которое приведет к желаемому результату и будет наиболее рациональным;

– проводить наблюдения, различного вида эксперименты;

– различными способами организовывать данные;

– грамотно выражать свои мысли (формулировать суждения);

– выдвигать гипотезу и проверять в частных случаях;

– находить контрпримеры;

– проводить доказательство;

– делать обобщающие заключения, выводы;

– представлять результаты исследования.

Специфические умения в области математики:

– выявлять существенные свойства понятий;

– устанавливать существование объекта;

– видеть динамику задачи;

– организовывать перебор;

– выявлять математические закономерности;

– находить закономерности: способ упорядочивания объектов, продолжение ряда объектов, наличие лишнего объекта;

– выявлять общие или аналогичные свойства объектов;

– формулировать, записывать в различных формах, математических моделях одно и то же утверждение;

– устанавливать отношения между понятиями;

– выделять понятия, свойства, теоремы, применимые к решению задачи, доказательству теоремы;

– обнаружение структурного сходства внешне различных систем (задач);

– устанавливать аналогию методов решений задач,

– разбивать задачу на подзадачи;

– строить алгоритм решения задачи, проблемы;

– находить различные варианты решения задач, доказательства теорем;

– проверять полноту решения и достаточность доказательств;

– выявлять избыточные и недостающие данные;

– видеть связь изучаемого материала с окружающей жизнью, с практической деятельностью людей, оценивать практическую значимость изучаемого материала;

– выполнять перенос знаний в другие ситуации;

– устанавливать границы применения новых знаний.

К инструментальным умениям на этапе бурного развития информационных технологий следует отнести не только умения работать с традиционными инструментами, с которыми в условиях математической учебной и иной деятельности чаще всего работаем, а именно: с линейкой, циркулем, транспортиром и др., но и умения работать с программным обеспечением универсального и специального
назначения:

– умения создавать текстовые документы, содержащие формулы, рисунки, чертежи, диаграммы, таблицы и пр.;

– умения создавать электронные расчетные таблицы;

– умения представлять результаты исследования с помощью презентационных программ;

– умения разрабатывать интеллект-карты с помощью таких программ как XMind, FreeMind и др.;

– умения работать в одной из так называемых интерактивных геометрических сред: GeoGebra, Математический конструктор, Живая математика и др.

Е.В. Баранова [15] выделяет следующие наиболее значимые дидактические функции учебных исследований:

1) открытие новых (неизвестных учащимся) знаний (установление существенных свойств понятия, выделение математических закономерностей, отыскание доказательств математических утверждений и т.п.);

2) углубление изучаемых знаний (получение определений, эквивалентных исходному, обобщение изученных теорем, нахождение различных доказательств изученных теорем и т.д.);

3) систематизация изученных знаний (установление отношений между понятиями, выявление взаимосвязей между теоремами, структурирование изученного материала и т.п.).

В результате проведенных нами исследований можно констатировать, что урок-исследование может быть уроком ознакомления с новым материалом, закрепления изученного, обобщения и систематизации знаний. Отметим, что при изучении понятий и теорем целесообразно проводить учебные исследования на этапах:

– выявления существенных свойств понятий, установления связей данного понятия с другими;

– ознакомления с фактом, отраженном в теореме, доказательства теоремы (в том числе и разными способами), обобщения теоремы, составления обратной теоремы и проверки ее истинности, установления связей изучаемой теоремы с другими.

Важнейшим средством развития учебно-исследовательских умений считают учебно-исследовательскую задачу.

Учебно-исследовательскую задачу относят к одному из видов проблемных задач. Учебно-исследовательская задача требует поиска, объяснения и доказательства закономерных связей и отношений экспериментально наблюдаемых или теоретически анализируемых фактов, явлений, процессов, в результате решения которых учащиеся открывают новое знание об объекте исследования, способе или средстве деятельности.

3.5.3. Структура урока-исследования

В структуре урока-исследования нами выше были выделены основные десять этапов. Исследователями в данной области [44, 85] установлено, что каждый из этапов исследования может быть реализован по-разному. Такая вариативность определяется разными причинами: спецификой предмета, изучаемой темой, дидактической целью урока, возрастом учащихся и др. Приведем примеры вариантов организации учебно-исследовательской деятельности на различных этапах урока-исследования.

1. Актуализация знаний. Готовясь уроку, учитель определяет, какое на этом уроке новое знание должно быть открыто: понятие, закономерность, правило, алгоритм, свойство или признак и т.п. Для открытия такого «нового знания» учащимся необходимо воспроизвести имеющуюся базовую информацию относительно изучаемого объекта. Например, чтобы получить правило умножения обыкновенных дробей, учащиеся должны понимать сущность таких категорий, как «обыкновенная дробь», «умножение», уметь моделировать величины, заданные обыкновенной дробью и т.д. Задача учителя в начале урока – актуализировать, т.е. дать возможность ученикам вспомнить имеющиеся у них теоретические знания, практические умения, навыки, опыт, необходимые для изучения нового материала.

2. Этап мотивации исследования и постановки проблемы исследования. Мотивацию исследовательской деятельности можно осуществить различными способами:

– предложить оригинальное или неожиданное задание;

– использовать исторический или занимательный материал (факты биографии математиков, математические фокусы и т.п.);

– заострить внимание на значимости ожидаемых результатов;

– использовать с целью теоретического обоснования задачи межпредметного, прикладного, профессионального и иного характера;

– сравнить различные математические тексты с целью доказательства эквивалентности предложений;

– использовать контекстные задачи, т.е. задачи, в условии которых описаны конкретные жизненные ситуации, явления, факты, интересные для учащихся. Требованием такой задачи является анализ, осмысление и объяснение заданной ситуации или выбор способа действия в ней, а результатом ее решения – встреча с учебной проблемой и осознание её личностной значимости. Контекстная задача призвана приблизить академическую абстрагированность условия задачи к реальной жизненной ситуации, помочь ученику найти своё собственное решение «задачи на смысл», осознать необходимость изучения математики, один из способов пробуждения у школьников познавательного интереса.

С помощью мотивационной задачи на уроке создаётся ситуация, которая требует от школьников применения соответствующих данной ситуации знаний и опыта. В ходе деятельности учащимися обнаруживается недостаточность имеющихся у них знаний. Наступает осознание проблемности сложившейся ситуации, что, в свою очередь, порождает вопросы. Это должны быть собственные вопросы ученика, на которые ему необходимо найти ответы для выхода из проблемной ситуации.

В реальной практике очень многим учащимся сложно самостоятельно сформулировать проблему. По этой причине проблемная ситуация должна быть продумана настолько тщательно, что каждый ученик мог бы подойти к формулированию проблемы урока через формулирование темы урока, цели урока или в виде вопроса. Деятельную помощь учащимся учитель может оказать, предлагая выполнить такие виды заданий:

– формулировка дополнительных вопросов к задаче: Сформулируйте к предложенной задаче ещё один или несколько вопросов;

– постановка вопросов к предложенной задачной ситуации: Поставьте вопросы к условию задачи. Что можно найти по предложенным данным?

– формулировка более общего или частного вопроса к содержанию предложенной задачи: Измените условие (требование) задачи так, чтобы вы могли её решить. Измените условие (требование) задачи так, чтобы с помощью её решения можно было найти ответ в каждом частном случае.

3. Сбор фактического материала. Исследовательская деятельность учащихся на уроке начинается с накопления информации. Сбор фактического материала зависит от вида данных и может осуществляться:

– при изучении соответствующей учебной или специальной литературы, источников информации сети Интернет и пр.;

– при наблюдении за свойствами каких-либо объектов, предложенных учащимся или демонстрируемых в виде выполненных статических, динамических и анимированных чертежей, анимации, фрагментов учебных видеофильмов и пр.;

– посредством проведения эксперимента, лабораторной работы в интерактивных геометрических средах. При этом считаем эксперимент тем методом исследования, который предполагает активное воздействие на объект исследования. Этим эксперимент принципиально отличается от наблюдения, не предполагающего такого воздействия;

– при организации практической работы исследовательского характера, в ходе которой учащиеся приходят к эмпирическим выводам, требующим теоретического обоснования;

– при решении серии исследовательских задач, цель которых – обнаружение закономерностей, требующих теоретического обоснования.

Прежде чем организовать изучение источников, наблюдение, эксперимент, важно поставить перед учащимися цель: установить, какие знания следует получить; за какими объектами, величинами, отношениями при этом следует наблюдать (например, как изменяется величина вписанного угла при изменении положения его вершины); проверить, при каких условиях существует изучаемый объект, выполняются те или иные свойства объекта; зачем нужно это знание, где оно в последующем будет использовано и др.

При планировании эксперимента следует тщательно продумывать ход испытаний, всевозможные пробы, попытки рассмотрения частных случаев, изменение числовых данных, рассмотрение предельных положений,
изменение взаимного расположения фигур или частей фигуры, каких-либо параметров. Испытания при проведении эксперимента не должны быть хаотичными, лишенными какой-либо логики, им необходимо задать направление посредством указаний, чертежей, по-
яснений и т.п.

4. Этап систематизации и анализа полученного материала. На этом этапе учащиеся осуществляют и совершенствуют основные мыслительные операции. Это сравнение, установление связей, классификация, обобщение, получение следствий; определение непротиворечивости, необходимости и достаточности условий.

Для оформления результатов наблюдения, эксперимента, решения задачи следует выбрать способ кодирования информации, получаемой в ходе наблюдения: запись в виде текста, построение графика, использование таблиц, диаграмм, схем, чертежей и т.п. для того, чтобы визуально представить обнаруженные в ходе исследования свойства, связи, соотношения, закономерности. Первоначально способ систематизации и представления фактического материала может быть указан учителем, в дальнейшем этот способ выбирается самим учеником.

5. Выдвижение гипотезы. Слово гипотеза происходит от древнегреческого hypothesis – основание, предположение, суждение о закономерной связи явлений. Гипотеза – это предположительное, вероятностное значение, ещё не доказанное логически и не подтверждённое опытом. Гипотеза – это мысленное представление основной идеи, к которой может привести исследование, предположение о результатах исследования. Выдвижение гипотез, предположений и нетрадиционных (провокационных) идей – важные мыслительные навыки, обеспечивающие исследовательский поиск и, в конечном счёте, прогресс в любой творческой деятельности.

Выдвижение гипотез может происходить как в процессе проведения испытаний или при систематизации фактического материала, так и в ходе выявления особенностей уже систематизированного фактического материала. Полезно прививать учащимся стремление записывать гипотезы на математическом языке, что придаст высказываниям точность и лаконичность.

Выдвижение гипотезы осуществляется посредством выделения общих свойств объектов, нахождения закономерностей (способ упорядочивания объектов, возможность продолжения ряда объектов, наличие лишнего объекта), высказывания предположений о возможности использовать определенные теоретические знания для решения поставленной задачи.

Для того чтобы научиться вырабатывать гипотезы, надо уметь задавать вопросы. Приведём примеры вопросов, тренирующих умение строить гипотезы:

– Почему …?

– Какова причина следующего явления?

– Что изменилось бы, если …?

– Чем отличается …?

– Какие условия необходимы для …?

– Какой вывод вы предлагаете сделать из предположения о …?

– Какой вывод вы предлагаете сделать из имеющихся фактов о …?

– Как вы относитесь к этому высказыванию …?

– Как это получается из …?

– Как взаимное расположение данных фигур влияет на вывод о том, что …?

– Можно ли выделить такие объекты … в нашем случае?

– Какими особенностями обладают данные объекты?

– Появились новые объекты, давайте их исследуем. Попытайтесь описать словами данные объекты. Какими особенностями они обладают?

– Какие вопросы вы хотели бы задать относительно данных фигур?

– Перечислите существенные признаки данного понятия. Какие при этом признаки можно считать несущественными …?

– Найдите возможную причину факта, свойства (равенства, параллельности, перпендикулярности, принадлежности и пр.).

В связи с появлением такого инструментария как ИГС математика стала предоставлять больше возможностей для осуществления данного этапа исследования. На уроке учащиеся с помощью ИГС могут генерировать различные гипотезы. Для этого учащимся предлагаются готовые модели или ставится задача конструирования нужной модели с помощью возможностей ИГС. Воздействуя на эти модели, учащимся удается находить некоторые закономерности, инварианты. Методика выдвижения гипотез может быть различной:

– после постановки проблемы ученикам предлагается самостоятельно выдвигать гипотезы возможного решения проблемы и сразу же их проверять;

– сначала учащимся предлагается решить серию однотипных задач, а затем ставится вопрос о выдвижении гипотез для объяснения наблюдаемых закономерностей.

На этапе выдвижения гипотез следует рассматривать любые предлагаемые для рассмотрения гипотезы, даже самые абсурдные. Подтверждать или опровергать их должны сами учащиеся. При этом недопустимо делать учащимся замечания типа «это неправильный ответ», «твоя гипотеза неверна», «такая формулировка не нравится», «этого не может быть». Важно стимулировать и поддерживать рассуждения учащихся при анализе выдвигаемых ими гипотез.

6. Проверка гипотезы. Проверка гипотезы может быть теоретической и экспериментальной. На этом этапе деятельность учащихся согласуется с образовательными целями и реализуется по сценарию, организуемому учителем.

Теоретическая проверка гипотезы предполагает соотнесение полученного результата с ранее известными фактами. В данной ситуации гипотезу может подтвердить или опровергнуть учитель, подтверждение гипотезы может быть найдено в учебнике.

Экспериментальная проверка может быть организована через:

– проведение вычислительного эксперимента;

– проведение компьютерного эксперимента;

– проведение проверки получения определенного результата при изменении параметров (значения коэффициентов, значения величин и др.) с помощью выполнения математических действий.

7. Доказательство истинности гипотезы. Этот этап заключается в проведении обоснований на основе имеющихся у учащихся теоретических знаний; в сравнении полученных результатов с имеющимися в соответствующей учебной литературе. На первых порах самостоятельный поиск и построение необходимых доказательств для многих учеников представляет значительные трудности. Для их предупреждения учителю важно предусмотреть всевозможные подсказки: здесь могут помочь наводящие вопросы, схематические изображения проблемной ситуации, чертежи с особыми пометками, подсказывающими идею доказательства и т.п. Идея доказательства может также зародиться в процессе выполнения испытаний, может возникнуть и при анализе систематизированного фактического материала, и на этом следует акцентировать внимание учащихся.

Мотивом доказательства гипотезы может служить напоминание, что опровергнуть гипотезу можно одним примером, для которого гипотеза не справедлива. И как бы много примеров, подкрепляющих гипотезу, не было бы обнаружено, для доказательства гипотезы этого недостаточно. А вдруг где-то найдётся контрпример? Есть ли уверенность, что гипотеза верна для любого случая?

8. Вывод по результатам исследовательской работы. Этот этап связан с формулированием обобщенных выводов и их письменным представлением также в обобщенной форме. Выводы могут включать установление границ применения новых знаний, а также непосредственном применение этих новых знаний в различных условиях или постановке новых вопросов и представлении результатов исследования.

9. Подведение итогов урока. Подведение итогов урока учителю следует провести в виде рефлексивного диалога, где учащиеся:

– высказывают собственные мысли, соображения, что способствует раскрытию личного субъектного исследовательского опыта;

– корректируют результаты учебно-исследовательской деятельности с учетом мнений других её участников;

– под управлением учителя развивают свои умения аргументировать идеи, слушать оппонентов, извлекать полезную информацию и делать необходимые выводы из предложений других членов группы, класса.

Важными компонентом на уроке является установка учащихся на кооперирование в решении исследовательских задач, а не на конкуренцию; создание в группе, классе отношений, подразумевающих доступность своего опыта для другого и открытость другого опыта для себя. Учитель при этом должен находиться внутри группы, быть не сторонним наблюдателем, а активным участником её деятельности, занимать сотворческую позицию.

Возможные вопросы для подведения итогов:

– С какими трудностями встретились? Что показалось наиболее трудным?

– Что помогло справиться?

– Можно ли было решить задачу другим способом?

– Что возьмёте на будущее из работы над задачей/заданием?

– Были ли ошибки? Какие? В чем причина ошибок?

– Как помочь себе избавиться от ошибок?

– Чему учились на уроке?

– Что помогало при этом?

– Можно ли по аналогии перейти к новой задаче? Что это за задача?

– Какие задания вы бы выбрали для самостоятельной (домашней) работы для своих товарищей?

10. Домашнее задание. Кроме решения задач на применение изученного понятия, метода и т.п. домашнее задание может содержать:

– самостоятельный поиск новых доказательств теорем, выводов новых формул, отыскание способов решения задач; при этом допустимо указать теоремы, идеи, методы, которые возможно использовать при решении;

– работу с дополнительной математической литературой, энциклопедиями, книгами по истории математики, использование информационных Интернет-ресурсов;

– проведение исследований, подготовку сообщений, проектов для выступления на факультативных занятиях, научно-практических конференциях.

Проведение урока-исследования требует тщательной подготовки, включающей разработку соответствующего методического обеспечения. Учитывая ответственность, с которой приходится подходить к подготовке и проведению подобных уроков, отметим определяющие дидактические принципы конструирования исследовательского урока [33]:

– реконструкция содержания учебного материала в комплекс исследовательских задач;

– организация продуктивного взаимодействия учителя и учащихся на основе актуализации личностных функций (выбор, оценка, рефлексия, прогноз); проектирование системы вопросов, ролей, действий.

Понимая важность учета указанных принципов при организации исследовательского обучения на примере уроков-исследований, рассмотрим подробнее их содержание.

3.5.4. Реконструкция учебного материала в комплекс исследовательских задач

Под исследовательской задачей будем понимать разновидность учебно-познавательной задачи, содержащей познавательное противоречие, процесс разрешения которого способствует формированию у учащихся исследовательских умений.

Учебно-исследовательская деятельность в области математики, по мнению ученых [16, 36, 44, 86, 88], связана с:

– введением новых для учащихся математических объектов и понятий;

– обоснованием существования или невозможности существования абстрактных математических объектов;

– сравнением математических понятий, установлением связей данного понятия с другими, классификацией математических объектов;

– нахождением свойств или признаков математических объектов;

– выявлением отношений между понятиями;

– нахождением закономерностей и зависимостей между метрическими характеристиками объекта;

– выяснением влияния одного или нескольких определенных условий на выполнение некоторого свойства объекта;

– классификацией геометрических объектов, отношений между ними, основных фактов из различных разделов геометрии;

– поиском различных способов решения, доказательства;

– ознакомлением с фактом, отраженным в формулировке или доказательстве теоремы;

– исследованием математических предложений;

– построением контрпримеров;

– составлением обратной теоремы и проверке ее истинности;

– обобщением и выделением частных случаев;

– составлением новых задач, вытекающих из решения данной;

– решением конструктивных задач различными способами;

– многовариантностью гипотез, способов решения, ответов;

– поиском новых способов действий, приёмов, догадок, эвристик;

– применением теоретических знаний к решению практических задач и т.д.

Анализ задачного материала школьных учебников геометрии показывает, что в них можно встретить исследовательские задачи:

– на нахождение некоторых свойств математических объектов, задачи типа «существует ли», «верно ли», «может ли»: «Существует ли треугольник со сторонами: а) 1 м, 2 м и 3 м; б) 1,2 дм, 1 дм и 4 дм?»;

– на поиск геометрических мест точек, задачи типа «что представляет собой»: «Что представляет собой множество всех точек плоскости, находящихся на данном расстоянии от данной прямой?»;

– с многовариантным ответом: «Найдите углы равнобедренного треугольника, если один из его углов равен 40°»;

– прикладного характера, например, «Два населенных пункта А и В находятся по одну сторону от прямой дороги. Где на дороге надо расположить автобусную остановку С, чтобы сумма расстояний от населенных пунктов до остановки была наименьшей?» [32, № 248, 283, 228, 303].

Очевидно, что для организации учебно-исследовательской деятельности такого набора задач недостаточно. Решить вопрос о составлении учебно-исследовательских задач могут помочь действующие школьные учебники. Путем преобразования задачи с закрытым условием в задачу с открытым условием, где требование не сформулировано в явном виде, задача из школьного учебника превращается в исследовательскую задачу. Так, задачи с явным требованием «Доказать» свойство (признак) некоторого математического объекта можно преобразовать в задачи с неявным требованием «Сколько ... ?»,
«Найдутся ли … ?», «Может ли … ?», «Для любого ли … ?» или в задачи неопределенного типа «Найти», «Исследовать» свойство или признак. Открытые формулировки задач «провоцируют» ученика на анализ данных, выдвижение и проверку гипотезы, то есть на осуществление элементов учебно-исследовательской деятельности, тогда как исходная задача была направлена лишь на построение логического обоснования предъявленного явно истинного математического утверждения.

Приведём несколько примеров реконструкции традиционных задач путем переформулирования требования, условия и постановки дополнительного исследовательского вопроса.

Задача 1 [32, № 110]. Докажите, что если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.

В требовании задачи в явном виде указан вид геометрической фигуры. Чтобы вид геометрической фигуры был неопределённым, следует переформулировать требование, например, так: Определите вид данного треугольника. Аналогично можно поступить и с условием задачи, если скрыть отношение между медианой и высотой. В результате получаем задачи 1А и 1Б.

Задача 1А с открытым требованием. Известно, что в треугольнике медиана совпадает с высотой. Определите вид данного треугольника.

Задача 1Б с открытым условием. Как в треугольнике АВС должна быть расположена высота ВН относительно медианы ВМ, чтобы он стал равнобедренным?

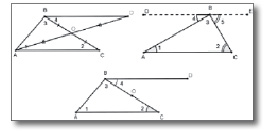
В процессе решения задачи 1А может быть первоначально проведен эксперимент в ИГС, где учащиеся на модели треугольника АВС, изменяя положение вершины В замечают, что треугольник становится равнобедренным в случае совпадения точек Н и М (см. рис. 139).

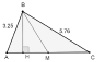
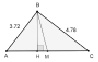
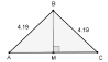
Рис. 139. Проведение эксперимента в ИГС

Дополнительными исследовательскими вопросами к задачам могут быть такие: Сформулируйте условие так, чтобы вид данного треугольника был равносторонним. Изменится ли вид треугольника, если медиану/высоту заменить на биссектрису?

Исследовательский характер многовариантных задач заключается в выделении по условию задачи всех возможных вариантов расположения данных элементов и поиск ответа в каждом отдельном случае. Получить многовариантную задачу можно, реконструируя условие снятием части характеристик (соответствие величин элементам фигуры, порядок следования) или их обобщением (например, заменой одного объекта на другой, более общий по сравнению с первым). Приведем примеры
реконструкции одновариантных задач по теме «Вписанная окружность» в многовариантные задачи.

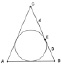
Задача 2 [32, № 689]. В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13. Найдите радиус окружности, вписанной в этот треугольник.

Убрав соответствие между сторонами и их величинами, получим:

Задача 2А. В равнобедренном треугольнике со сторонами 10 и 13 см найдите радиус окружности, вписанной в этот треугольник.

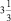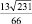По условию полученной задачи можно построить 2 чертежа (см. рис. 140, а), и она будет иметь два разных решения: или см.

Задача 3 [32, № 690]. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см, считая от основания. Найдите периметр треугольника.

Опустив порядок следования, получаем:

Задача 3А. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см. Найдите периметр треугольника.

Опять получаем 2 альтернативных чертежа (см. рис. 140, б).

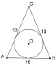
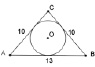
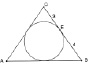
а б

Рис. 140. Чертежи к условиям задач 2 и 3

Учебники геометрии содержат немало задач и теорем, допускающих использование дополнительных построений и имеющих несколько способов решения/доказательства. Для поиска и исследования этих способов может быть использовано задание типа: «Докажите …, используя дополнительные построения, представленные на рисунках. Что общего в данных дополнительных построениях? Как можно догадаться именно об этом способе доказательства? Можно ли запомнить этот способ/приём доказательства?

Рассмотрим, например, свойство биссектрисы треугольника.

Задача 4 [32, № 535]. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Переформулируем задачу введением подсказок в виде чертежей к решению и постановкой дополнительных вопросов.

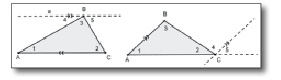
Задача 4А. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, используя дополнительные построения, показанные на рис. 141. Что общего в предложенных дополнительных построениях? Использование каких теорем «подсказывает данное дополнительное построение»?

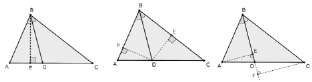
Рис. 141. Дополнительное построение – высота

Или другой вариант формулировки

Задача 4Б. Сформулируйте гипотезы о способах доказательства свойства биссектрисы треугольника.

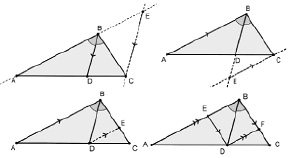
Рис. 142. Дополнительное построение – параллельная прямая

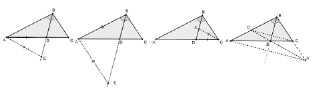
Рис. 143. Дополнительное построение – равнобедренный треугольник

Первый чертеж, представленный на рис. 141, соответствует доказательству, которое дано в учебнике [32, §1 Гл. VII ]. Два других закрепляют идею доказательства:

1) использование теорем об отношении площадей треугольников, имеющих равные высоты (углы);

2) дополнительное построение – высота треугольника соответствуют идее доказательства, основанной на использовании понятия подобных треугольников и их признаков, что является предметом изучения школьниками следующего параграфа.

Задача 4В. Можно ли доказать свойство биссектрисы треугольника с помощью дополнительного построения – описанной около данного треугольника окружности (см. рис. 144)?

Постановка задач на исследование геометрических конструкций с использованием ИГС помогает выявить неопределенность условия, способы его реализации, исследовать задачи со сложной конструкцией, найти лишние данные и формулировать обобщённые задачи, так как динамическая модель, выполненная по данным задачи, позволяет изменять значения величин и взаимное расположение отдельных элементов чертежа.

Приведём пример задачи с избыточными данными и исследовательское задание, которое можно выполнить в ИГС.

Задача 5 [№ 8б, с. 135, 98]. В треугольники АВС и СDA (В и D по одну сторону от СА) вписаны окружности. Найдите длину общей внешней касательной к этим окружностям, если АВ = 7, ВС = CD, DA = 9.

Задача 5А. Исследуйте аналогичную геометрическую конструкцию, в которой точки В и D находятся по разные стороны от СА.

Эксперимент, проведенный в ИГС с данной конструкцией, показывает, что ответ не только не зависит от длины отрезков АС, ВС и СD, но и не зависит от взаимного расположения точек B, D и прямой СА, что позволяет снять некоторые условия данной задачи и дать ей более общую формулировку.

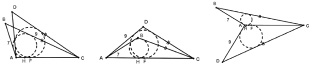
Рис. 145. Динамическая модель к задаче 5

Следующий пример – с противоречивыми данными, определить которые тоже можно с использованием ИГС.

Задача 6 [№ 690, 32]. Прямые АВ и АС – касательные к окружности с центром О, В и С – точки касания. Через произвольную точку Х, взятую на дуге ВС, проведена касательная к этой окружности, пересекающая отрезки АВ и АС в точках М и N. Докажите, что периметр треугольника АМN и угол MON не зависят от выбора точки Х на дуге ВС.

Задача 6А. Прямые АВ и АС – касательные к окружности с центром О, В и С – точки касания. Через произвольную точку Х, взятую на дуге ВС, проведена касательная к этой окружности, пересекающая отрезки АВ и АС в точках М и N. Исследуйте зависимость периметра треугольника АМN и угла MON от выбора точки Х на дуге ВС.

Исследовательский потенциал содержится и в обучении учащихся составлению задач: «Новые понятия и свойства математических объектов являются предметом специального исследования: какие задачи могут быть составлены на их основе? Какие новые связи при этом появляются?» [101].

Рассмотрим пример задачи, построение модели которой в ИГС позволяет определить не только избыточность условия, но и поставить новые вопросы к условию.

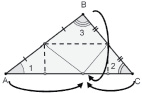
Задача 7. В треугольнике АВС АВ = 12, ВС = 5, СА = 10. Точка D лежит на прямой ВС так, что BD : DC = 4 : 9. Окружности, вписанные в треугольники ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка EF.

Неопределенность в условии данной задачи показана на рис. 146.

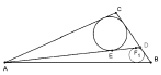
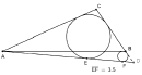
Рис. 146. Два альтернативных чертежа к условию задачи 7

Построение динамической модели данной задачи в ИГС таким образом, что положение точки D можно изменять, дает возможность увидеть, что длина отрезка EF во втором случае не изменяется. То есть данная задача имеет избыточное условие BD : DC = 4 : 9 для второго случая[26]. При этом сама ситуация порождает несколько вопросов исследовательского характера:

– чему равна длина отрезка EF, если точка D лежит на прямой BС вне одноименного отрезка;

– в каком отношении должны быть BD и DC, чтобы окружности, вписанные в треугольники ADC и ADB, касались друг друга?

Сформулированные вопросы порождают новые задачи (см. рис. 147).

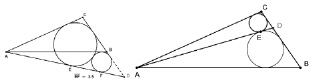
Рис. 147. Касание окружностей

Табл. 24 демонстрирует примеры реконструкции теоретического и задачного материала к уроку по теме «Сумма углов треугольника».

Таблица 24

Примеры реконструкции содержания учебного материала по теме
«Сумма углов треугольника» в серию исследовательских задач[27]

Источниками исследовательских задач и идей их составления служат различные дидактические материалы, рабочие тетради к учебникам, пособия для учителей [35, 84, 94, 101] и пр.

3.5.5. Организация учебно-исследовательской деятельности
на уроке-исследовании

Исследования Е.В. Барановой и М.И. Зайкина показывают, что организация учебных исследований при изучении понятий наиболее эффективна на этапе установления связей данного понятия с другими, так как позволяет ввести полученные новые знания в систему уже известных ранее знаний. При изучении теорем учебные исследования целесообразны при ознакомлении с фактом, отражённом в теореме, доказательстве теоремы и установлении её связи с другими математическими фактами. В качестве методического обеспечения они предлагают использовать учебно-исследовательские карты. Такие карты состоят из фрагментов учебного материала, соответствующих основным этапам учебного исследования. Например, такие этапы: 1 – задача, 2 – проблема, 3 – пробы, 4 – таблица результатов, 5 – гипотезы, 6 – проверка гипотез, 7 – доказательство (опровержение) гипотез. Карты представляют собой фрагментарный текст, часть которого учащимся следует записать самостоятельно. В зависимости от возможностей ученика, соотношение текста и пропусков в карте может варьироваться. Примеры учебно-исследовательских карт по темам «Отрезок», «Прямоугольник», «Многоугольник» приведены в статьях авторов [15, 16], а в рамках данной работы – на рис. 148.

Использование учебно-исследовательских карт уменьшает затруднения, возникающие у учащихся при выполнении исследовательских заданий, поскольку такие карты выполняют роль алгоритмических предписаний и рекомендаций, задающих учащимся этапы или направления их деятельности.

Эффективным дидактическим средством развития самостоятельной познавательной деятельности учащихся являются, по мнению В.И. Тараник [86], задания для организации практических работ по геометрии, удовлетворяющие требованиям:

– постановка вопроса в задаче должна быть такой, чтобы ответ на него предполагал проведение исследования;

– условие задачи должно предполагать рассмотрение различных геометрических конфигураций, использование различных методов и способов решения;

– в условиях задачи должны отсутствовать прямые указания на использование известных теорем и формул;

– содержание задачи определяет необходимость самостоятельной познавательной деятельности.

Автором разработан комплекс заданий, включающих задания пяти типов:

– формирование понятий и усвоение их определений;

– выдвижение следствий из факта принадлежности объекта объему понятия;

– формулирование, усвоение, «переоткрытие» формулировок теорем и их доказательства;

– выдвижение гипотез, их доказательство и опровержение;

– усвоение методов решения задач.

Представим пример организации и проведения практической работы по теме «Сумма углов треугольника», которая демонстрирует одну из форм проведения экспериментальной работы при обучении математике. Целью этой экспериментальной работы является наглядное подтверждение выводов науки, указание на связь учебного материала с окружающей действительностью.

а

б

Рис. 148. Примеры учебно-исследовательских карт по организации
опытно-индуктивных (слева) и дедуктивных исследований (справа)

Практическая работа.

1. Начертите три треугольника – остроугольный, прямоугольный, тупоугольный.

2. Перечертите с доски таблицу (см. табл. 25).

Таблица 25

Образец таблицы к заданию

3. Измерьте каждый угол начерченных треугольников, и результаты измерения занесите в соответствующую графу таблицы. Измерение производить с точность до одного градуса.

4. Найдите сумму внутренних углов.

5. Сравните результаты измерений по каждому треугольнику и сделайте вывод.

К моменту окончания практической работы учитель либо сам составляет на доске сводную таблицу результатов измерений нескольких учащихся (см. табл. 26), либо предлагает внести данные своих измерений учащимся, выполнивших задание ранее других.

Таблица 26

Сводная таблица результатов измерений учащихся

Вписав в таблицу результаты, учитель организует с классом эвристическую беседу по анализу полученных данных.

Примерные вопросы для эвристической беседы

1. Чему примерно равна сумма углов остроугольного треугольника? прямоугольного треугольника? Чему равна сумма углов тупоугольного треугольника?

2. Какой можно сделать вывод о сумме внутренних углов треугольника? Зависит ли сумма внутренних углов треугольника от формы фигуры? От чего она еще не зависит?

3. Чем объяснить небольшие отклонения от 180°, которые имели место в нашем эксперименте?

4. Вас в классе 25 человек; вы начертили всего 75 треугольников. Следовательно, если принять во внимание неточность измерений, то можно утверждать, что каждый из 75 треугольников обладает свойством, которое мы подметили. Но тогда возникает вопрос: будет ли найденный нами вывод верен для всех треугольников? Таким образом учащихся подводим к принятию необходимости проведения доказательства справедливости полученного вывода для всякого треугольника, независимо от его размеров и формы. Далее учитель совместно с учащимися дает точную формулировку теоремы, записывает на доске условие и заключение теоремы, проводит доказательство.

Организацию решения учебно-исследовательских задач младшими подростками И.В. Клещёва предлагает осуществить в игровой форме [44]. Автором описан следующий интересный приём организации решения определенной учебно-исследовательской задачи. На отдельных карточках предлагаются некоторые возможные шаги (некоторые математические и логические операции) для решения данной задачи. Каждая карточка содержит один шаг. Учащиеся должны выбрать подходящие карточки, составить из них цепочку, указывающую на последовательность действий, в результате выполнения которых задача будет решена. Выполнение подобных заданий можно организовать в небольших группах по 4–5 человек при решении не очень сложных исследовательских задач. Например, решение исследовательской задачи на обнаружение свойства равенства вертикальных углов сопровождается выдачей учащимся карточек с заданиями в произвольном порядке. Карточки содержат описания таких действий:

– Нарисуйте равные углы.

– Нарисуйте смежные углы.

– Нарисуйте несколько пар вертикальных углов.

– Измерьте транспортиром каждый из вертикальных углов. Сравните градусные меры вертикальных углов в каждой паре.

– Нарисуйте не равные между собой вертикальные углы.

– Сформулируйте гипотезу о свойстве вертикальных углов.

– Объясните свою гипотезу.

Некоторые карточки не имеют прямого отношения к поставленной задаче. Учащимся необходимо выбрать только подходящие карточки, что способствует развитию умений прогнозировать, планировать, анализировать, обосновывать, оценивать, выделять существенное.

Другой пример – игра «Чёрный ящик». Организуется для осуществления поиска математического объекта с заданными свойствами, содержит возможности пропедевтики нахождения необходимых и достаточных условий существования математических объектов. Суть игры состоит в том, что ведущий (учитель или ученик), загадывает некоторый математический объект. Сам объект или его название фиксируется ведущим на листе бумаги, и этот лист бумаги ведущий прячет в «чёрный ящик». Далее игра может развиваться по двум сценариям. Первый вариант: ведущий изначально описывает игрокам все свойства объекта, необходимые для его определения, игроки не могут уточнять дополнительные свойства, а только называют предполагаемые варианты до тех пор, пока не отгадают заданный объект. Второй вариант: ведущий дает некоторую подсказку об объекте, например, одно из свойств, затем игроки называют по одному из возможных свойств загаданного объекта, а ведущий определяет, обладает ли объект названным свойством или не обладает. После этого игрок может попробовать назвать сам объект. Например, на уроке в 8 классе учитель проводит описанный во втором варианте игровой момент:

– Я начертил трапецию на листе бумаги. Задайте только один вопрос и, выслушав ответ, скажите, будет ли она равнобокой.

Учащиеся могут задать вопросы:

– Будут ли углы при основании равны?

– Будут ли диагонали равны?

Ученик, задавший вопрос, должен обосновать его, то есть доказать, что при утвердительном ответе трапеция будет равнобокой, а при отрицательном – не будет. Выигрывает игрок, назвавший загаданный объект. После этого полезно определить минимальный набор свойств, характеризующих объект.

Т.Ф. Сергеева [81] в организации учебно-исследовательской деятельности школьников в процессе обучения геометрии с использованием ИГС выделяет два этапа – репродуктивный и продуктивный, которые характеризуются различными видами деятельности учащихся и типами заданий.

Этап 1. Репродуктивный

На этом этапе можно организовать:

– просмотр видеодемонстраций, используемых в качестве наглядной основы для формирования представлений о геометрических объектах, их сущностных характеристиках, свойствах и отношениях между ними. Знакомство с инструментами ИГС;

– перевод наглядных представлений в плоскость теоретических знаний о геометрических объектах, их свойствах и отношениях.

К возможным типам заданий на данном этапе можно отнести:

– пассивное наблюдение видеодемонстрации и знакомство с понятиями, определениями, признаками, свойствами и отношениями геометрических объектов (1);

– задания на воспроизведение операций чертежной плоскости в соответствии с увиденным образцом (2);

– задачи на определение геометрического объекта при помощи родового и видового отличия в процессе динамического моделирования (3);

– применение комплекса изученных операций и знаний о свойствах геометрических объектов (4).

Приведём примеры соответствующих заданий и задач из электронного издания «Наглядная планиметрия. 7 класс», предназначенного для организации учебно-исследовательской деятельности с использованием интерактивной геометрической среды GeoGebra.

Пример 1. Видеодемонстрации понятий, сопровождаемые формулировками определений и алгоритмом использования инструмента ИГС для его построения изображения рассматриваемого понятия (см. рис. 149).

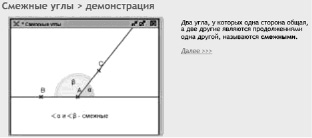
Рис. 149. Видеодемонстрация смежных углов

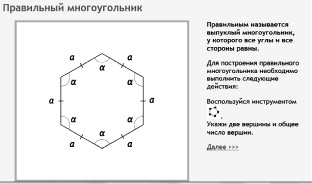
Рис. 150. Видеодемонстрация правильного многоугольника

Пример 2.1. Даны четыре точки. Постройте вертикальные углы, стороны которых проходят через данные точки.

Пример 2.2. Постройте ромб такой, чтобы данный угол был одним из углов ромба, а одна из сторон была равна длине данного отрезка.

Пример 2.3. Проверьте утверждение: около любого правильного многоугольника можно описать окружность, и притом только одну.

Пример 3.1. Проведите три луча с общим началом. Назовите углы, образованные этими лучами.

Пример 3.2. Используя данные чертежи (см. рис. 151), получите изображение параллелограмма.

Пример 4.1. Верно ли утверждение, что сумма смежных углов равна 180°?

Пример 4.2. Как определить, является ли четырёхугольник параллелограммом? Проверьте, являются ли эти четырёхугольники параллелограммами.

Пример 4.3. Исследуйте вопрос о том, как расположен отрезок, соединяющий середины боковых сторон относительно оснований трапеции.

Пример 4.4. Исследуйте вопрос о том, можно ли описать окружность около многоугольника, который является равносторонним, но не равноугольным.

Рис. 151. Динамические чертежи электронного издания
«Наглядная планиметрия. 8 класс»

Этап 2. Продуктивный

На этом этапе происходит:

– выдвижение гипотез в процессе исследования и экспериментирования с динамическими моделями геометрических объектов как основа для постулирования и доказательства утверждений геометрии;

– решение задач с использованием динамического моделирования, способ решения которых заранее неизвестен или требует нестандартных подходов к анализу условий задачи (для которых нельзя построить чертеж, исходя только из условий, содержащихся в тексте задачи).

К возможным типам заданий на данном этапе можно отнести:

1) задачи, требующие самостоятельного формулирования гипотезы;

2) задачи на выявление граничных условий, анализа единственности (множественности) вариантов выполнения построения;

3) задачи с заранее неизвестным ответом.

Пример 1.1. Исследуйте вопрос о том, сколько в треугольнике может быть прямых углов, тупых углов, острых углов.

Пример 1.2. Исследуйте вопрос о виде трапеции, если её диагонали равны.

Пример 1.3. Постройте правильный шестиугольник и шесть квадратов на его сторонах вне шестиугольника. Исследуйте вопрос о виде многоугольника, образованного вершинами квадратов, не совпадающих с вершинами шестиугольника.

Пример 2.1. Дан луч и отрезок. Постройте вертикальные углы, стороны которых содержат данные луч и отрезок. В каком случае задача не имеет решения?

Пример 2.2. Постройте параллелограмм с диагоналями, равными длине данных отрезков. Сколько решений имеет задача?

Пример 3.1. Придумайте способ построения прямого угла без использования инструментов «Перпендикуляр» и «Перпендикулярная прямая».

Пример 3.2. Придумайте способ построения ромба.

Пример 3.3. Как из правильного шестиугольника получить: восемь равных трапеций; шесть равных трапеций.

Основой организации взаимодействия на исследовательском уроке, по мнению Н.И. Голавской [33], является учебный диалог. Под учебным диалогом понимается создание ситуаций общения с целью разрешения учеником проблемы и поиска личностного смысла, содержащегося в изучаемом материале. Средствами активизации участия школьников в учебном диалоге являются:

– проблемные вопросы, которые у учащиеся вызывают затруднения, возможность неоднозначного ответа;

– анализ рассуждений сверстников, письменных работ учащихся, выполненных чертежей, моделей. Например, «Чьё рассуждение является правильным? Обоснуй свою точку зрения»;

– анализ противоречивых высказываний, решений (ученых, педагогов, писателей, философов, политиков). Например, «Какой ответ не верен? Объясните появление ошибки в решении»;

– незаконченное доказательство, решение задачи, эксперимент. Учащиеся заканчивают его по-своему, а затем результаты сравниваются и проверяются.

О некоторых идеях, набросках учебных исследований можно ознакомиться в статье Л.Э. Орловой [67].

Формами организации исследовательской деятельности учащихся являются:

– индивидуальная работа;

– работа парах (например, пара «теоретик-практик» при организации исследовательской работы в ИГС);

– работа в группах;

– коллективная (фронтальная) работа.

В зависимости от участия учителя в процессе исследования, можно выделить следующие виды уроков-исследований:

– знакомство учащихся с процессом исследования на уроках «Образец исследования»;

– отработка отдельных приёмов учебно-исследовательской деятельности на уроках «Элементы исследования»;

– использование исследовательского подхода в процессе обучения на уроках «Исследование».

В табл. 27 представлен вариант организации деятельности и выбора формы работы на исследовательских уроках разного уровня.

Таблица 27

Организация деятельности на уроке-исследовании

3.5.6. Конспект урока-исследования по теме
«Неравенство треугольника»

Цель урока: исследовать связь между сторонами треугольника и найти применение новому знанию.

Тип урока: урок изучения нового материала.

Оборудование: компьютеры, интерактивная доска, рабочие тетради для исследовательских работ.

План урока

1. Актуализация опорных знаний: решение задач на готовых чертежах по теме «Соотношения между сторонами и углами треугольника».

2. Мотивация и постановка проблемы исследования: решение конструктивной задачи в ИГС.

3. Эксперимент по исследованию зависимости сторон треугольника в ИГС (парная работа).

4. Выдвижение и проверка гипотезы.

5. Доказательство теоремы неравенства треугольника (групповая работа).

6. Вывод по результатам исследовательской работы.

7. Домашнее задание.

Ход урока

1. Актуализация опорных знаний

В ходе фронтального опроса организуется повторение учащимися знаний и умений на соотношения между сторонами и углами треугольника, сравнение катета и гипотенузы прямоугольного треугольника, свойство и признак равнобедренного треугольника с помощью заданий:

Задача 1. Найдите соответствие между сторонами треугольника и их длинами, если известны величины углов.

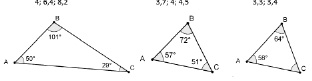
Рис. 152. Иллюстрация к задаче 1

Задача 2. Найдите соответствие между углами треугольников и их величинами, вычислите недостающие величины, если известны длины сторон данных треугольников.

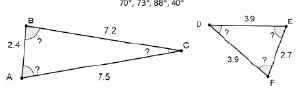
Рис. 153. Иллюстрация к задаче 2

2. Мотивация и постановка проблемы исследования

Учащимся предлагается задача 3: Ученик 7 класса Иван Иванов построил в интерактивной геометрической среде треугольник, две стороны которого равны 4 и 1, длина третьей стороны тоже выражается целым числом. Может ли эта сторона равняться 1? 2? 3? 4? 5? 6?

Учащиеся могут предложить построить треугольники с заданными сторонами в ИГС. Учителю следует обратить внимание учащихся на способ решения. Если такой треугольник существует, то его можно построить, и пример этого треугольника может служить доказательством. Если же такой треугольник не существует, следует объяснить, почему треугольник с заданными сторонами нельзя построить.

Итогом работы должна быть сформулированная учащимися проблема: Существует ли зависимость между длинами сторон треугольника? Если существует, то какая?

3. Эксперимент по исследованию зависимости сторон треугольника в ИГС

Учащимся предлагается найти нужную закономерность с помощью ИГС. Данную работу учащимся предлагается выполнять в парах.

Эксперимент. Исследуйте в ИГС модель треугольника со сторонами a и b. (В данной модели вы можете изменять положение вершин треугольника, измерять третью сторону треугольника, изменять длины данных сторон треугольника с помощью одноимённых ползунков).

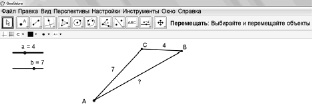
Рис. 154. Модель треугольника
с фиксированными сторонами, выполненная в ИГС GeoGebra

Опыт 1. Пусть в треугольнике АВС ВС = a = 4 и АС = b = 7. Измерьте длину стороны с. Измените положение точек А и В. Снова измерьте длину стороны с. Повторите проделанное ещё раз. Данные занесите в таблицу и сделайте вывод:

Опыт 2. Измените длины сторон АС и ВС треугольника АВС. Повторите опыт. Данные занесите в таблицу и сделайте вывод:

Опыт 3. Измените ещё раз длины сторон АС и ВС треугольника АВС. Повторите опыт. Данные занесите в таблицу:

4. Выдвижение и проверка гипотезы

Гипотеза. В треугольнике ______ сторона _____ суммы двух других сторон.

Проверка гипотезы.

Опыт 4. Постройте в ИГС произвольный треугольник АВС. Измерьте его стороны. Данные занесите в таблицу:

5. Доказательство истинности гипотезы (групповая работа)

Для нахождения способа доказательства теоремы, класс разбивается на группы. Группам предлагается выбрать один из вариантов чертежа (см. рис. 155 и 156) и с его помощью доказать гипотезу. Ключевым в доказательстве теоремы в обоих вариантах является дополнительное построение, а чертёж выступает в роли подсказки к его поиску.

Вариант 1

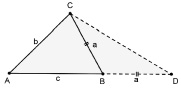
Рис. 155

Вариант 2

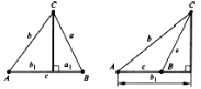
Рис. 156

По окончании работы группы представляют свои доказательства с обоснованием роли дополнительного построения в доказательстве теоремы (в первом варианте удлинение стороны с на длину, равную а, позволяет сравнить b и (c + a) как стороны, противолежащие углам треугольника; во втором варианте построение высоты дает возможность сравнить катет с гипотенузой, то есть свести доказательство новой теоремы к теоремам, доказанным ранее).

6. Вывод по результатам исследовательской работы о применении полученных знаний

Результатом работы должно явиться «открытие» теоремы: её формулировка и отыскание идеи её доказательства. Окончательные выводы о проделанной учениками работы производятся в процессе ответов на следующие вопросы учителя:

– Сформулируйте доказанную теорему. Данная теорема называется неравенством треугольника.

– Что общего в вариантах доказательства теоремы?

– Как запомнить, какое дополнительное построение надо выполнить для доказательства теоремы?

– Какую роль играют применяемые в доказательстве дополнительные построения?

– Как сформулировать подобную теорему для любых трёх точек?

– Вернёмся к задаче 3. Почему сторона треугольника не может быть раной 5? 6? Может ли сторона равняться 3? 2? Почему?

– Будет ли выполняться аналогичное свойство для любого треугольника? Сформулируйте свойство для произвольного треугольника.

– Какой вопрос к задаче 3 следует поставить, чтобы ответ звучал так: «Больше 3, но меньше 5»?

– Какие задачи можно ещё решать с использованием теоремы о неравенстве треугольника? Сформулируйте несколько таких задач (задачи на определение существования треугольника, доказательство геометрических неравенств и др.).

7. Домашнее задание. Теорема о неравенстве треугольника и её следствия (с доказательствами). Задачи на определение существования треугольника, доказательство геометрических неравенств с использованием дополнительных построений (удлинение стороны, проведение перпендикуляра).