Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

1.2. Описание структуры полимеров в рамках фрактального анализа

Теория фракталов и ее приложения к различным физическим и химическим процессам получили в последние годы широкое распространение [26-34]. Для облегчения понимания представленных в настоящей монографии результатов приведем основные понятия и определения фрактального анализа применительно к описанию структуры полимеров.

Фракталами называют самоподобные объекты, инвариантные относительно локальных дилатаций, т.е., самоподобные объекты. Понятие о фракталах как о самоподобных множествах ввел Мандельброт [26], определив фрактал как множество, для которого размерность Хаусдорфа-Безиковича всегда превышает топологическую размерность. Фрактальная размерность d_f объекта, внедренного в d-мерное евклидово пространство, изменяется от 1 до d. Фрактальные объекты являются естественным заполнением множеств между известными евклидовыми объектами с целочисленными размерностями 0, 1, 2, 3, ... . Большинство существующих в природе объектов оказались фрактальными, что и явилось основной причиной бурного развития методов фрактального анализа [33].

Согласно классификации Фемили [35], фрактальные объекты можно разделить на два основных типа: детерминистические и статистические (случайные). Детерминистическими фракталами являются самоподобные объекты, которые точно конструируются на основе некоторых базовых законов. Типичными примерами таких фракталов являются множество («пыль») Кантора, кривая Кох, ковер Серпинского, снежинка Вичека и др. Наиболее важны два свойства детерминистических фракталов: возможность точного расчета фрактальной размерности и неограниченный интервал их самоподобия (- ∞; + ∞). Поскольку линию, плоскость или объем можно разделить на бесконечное число фрагментов различными способами, то возможно построить бесконечное число детерминистических фракталов с различными фрактальными размерностями. Поэтому детерминистические фракталы нельзя классифицировать без введения дополнительно к фрактальной размерности других их параметров [33].

Статистические фракталы порождаются беспорядочными (случайными) процессами. Элемент беспорядочности характерен для большинства реальных физических явлений и объектов. Факт достаточности выполнения условия беспорядочности, т.е., отсутствия какой-либо пространственной корреляции, для образования фракталов впервые был отмечен Мандельбротом [26]. Типичным примером такого фрактала является траектория статистического блуждания. Однако чисто статистические модели часто неадекватно описывают реальные физические системы. Одной из причин этого является эффект исключенного объема. Суть данного эффекта заключается в геометрическом ограничении, запрещающем двум разным элементам системы занимать один и тот же объем пространства. Это ограничение должно учитываться в соответствующих модельных построениях [36]. Наиболее известными примерами таких моделей, являются блуждания без самопересечений, «решеточные звери» и статистическая перколяция [33].

В определенном интервале масштабов фракталы имеют различные топологические структуры в зависимости от максимального числа элементов, которые соединяются с данным элементом системы. Если каждый элемент можно связать максимум с двумя другими, то полученная структура не имеет ответвлений. По аналогии с линейными полимерами Фемили [35] назвал этот тип фракталов линейным. Если происходит ветвление, то результирующий фрактал имеет каркасоподобную структуру: такой тип фракталов был назван разветвленным.

Микроструктура полимеров может обладать высокой степенью естественного или создаваемого искусственно самоупорядочения [37], что является одним предельным случаем. Другой предельный случай - это хаос (противоположность порядка). Во фрактальном анализе рассматриваются промежуточные варианты - между полным порядком и полным хаосом. Как правило, такие системы получают в условиях, далеких от термодинамического равновесия и они заполняют промежуток между периодическими структурами и полностью разупорядоченными системами [38; 39]. Иначе говоря, фрактальные структуры должны обладать определенным уровнем промежуточного порядка. Поэтому при изучении термодинамически неравновесных твердых тел (которыми, как правило, являются полимеры [40]), обладающих локальным порядком [8], важен вопрос о взаимосвязи уровня локального порядка структур и степени их фрактальности [9].

В настоящее время нет сомнений в том, что приближение сплошной среды не может служить адекватной моделью для реальных полимеров [9; 30; 32; 41]. Уже при синтезе полимеров в них появляется множество микро-, мезо- и макродефектов, которые могут развиваться в процессе эксплуатации. Более того, эмпирически установлено [29; 42; 43], что при деформировании даже изначально однородных сред они приобретают иерархическую блочную структуру, характерные пространственные масштабы которой L_i с достаточной степенью точности удовлетворяют соотношению [29]:

                                             (1.12)

где Λ_i - коэффициент автомодельности; i = 0, 1, 2, ...

Природные фракталы, такие как облака, полимеры, аэрогели, пористые среды, дендриты, коллоидные агрегаты, трещины, поверхности разрушения твердых тел и т.п., обладают лишь статистическим самоподобием, которое к тому же имеет место только в ограниченном интервале пространственных масштабов [26; 27; 29; 30; 31; 34]. Для твердых полимеров экспериментально показано [44], что такой интервал составляет от нескольких ангстрем до нескольких десятков ангстрем.

Взаимосвязь уровня локального порядка и степени фрактальности неупорядоченных твердых тел можно описать общими математическими терминами [45]. В частности, говоря о структуре тверды полимеров, следует отметить, что большинство исследователей считают доказанными наличие в них структурных образований сегментального масштаба. Следует подчеркнуть, что представление об аморфном состоянии как об абсолютно неупорядоченном некорректно. Согласно теореме Рамсея [29; 46] любое достаточно большое число i > R(i, j) точек или объектов (в рассматриваемом случае - элементов структуры) обязательно содержит высокоупорядоченную систему из N_j ≤ R(i, j) элементов. Поэтому абсолютно неупорядоченных систем (структур) не существует. Аналогично можно показать, что любая структура , состоящая из N элементов, при N_j > B_N(j) представляет собой совокупность конечного числа k ≤ j вложенных друг в друга самоподобных структур, Хаусдорфова размерность которых в общем случае может быть разной. Это значит, что любая система независимо от физической природы, состоящая из большого числа элементов, является мультифракталом ( в частном случае - монофракталом) и характеризуется спектром размерностей Реньи d_q, q = - ∞  ÷ ∞ [45]. Стремление конденсированных систем к самоорганизации в масштабно-инвариантных мультифрактальных формах является следствием фундаментальных систем, а d_q определяются конкуренцией близко- и дальнодействующих межатомных взаимодействий, определяющих объемную сжимаемость и сдвиговую жесткость твердых тел соответственно [47]. А так как топология структуры оказывает на физико-химические свойства полимеров фундаментальное влияние, то для изучения их реальной структуры можно использовать результаты физико-механических исследований [46; 48].

Еще одним очень важным свойством фракталов, отличающим их от традиционных евклидовых объектов, является необходимость определения по крайней мере трех размерностей: d - размерности объемлющего евклидова пространства, d_f - фрактальной (Хаусдорфовой) размерности и d_s - спектральной (фрактонной) размерности, характеризующей связность объекта [49]. (Для евклидовых пространств d_f = d_s = d, и это обстоятельство позволяет рассматривать евклидовы объекты как частный («вырожденный») случай фрактальных. Это означает, что для описания структуры фрактальных объектов (например, полимеров) даже при фиксированной величине d требуются две фрактальные размерности - d_f и d_s. Такая ситуация соответствует положению неравновесной термодинамики, согласно которому для описания термодинамически неравновесных твердых тел (полимеров), для которых не выполняется критерий Пригожина-Дефая, необходимы, как минимум, два параметра порядка [40; 50].

Для применения в исследованиях структуры и свойств полимеров методов фрактального анализа и принципов синергетики существует ряд предпосылок. Во-первых, аморфные стеклообразные полимеры характеризуются термодинамически неравновесной структурой [51]. Шефер и Кефер [52] показали, что фрактальные структуры формируются в ходе неравновесных процессов. Поэтому есть все основания полагать наличие в стеклообразных полимерах фрактальных структур [33]. Такое предположение неоднократно подтверждалось экспериментально [44; 53-56].

Например, низкочастотная часть спектра неупругого рассеяния света в аморфных полимерах представляет собой широкое бесструктурное плато [44]. Такая особенность спектра связана с фрактальностью структуры полимеров на малых линейных масштабах [44; 55].

Фрактальные объекты характеризуются следующим соотношением между массой М (или плотностью r) и линейным масштабом измерения L^и [26]:

,                                                    (1.13)

где d_m - показатель скейлинга массы.

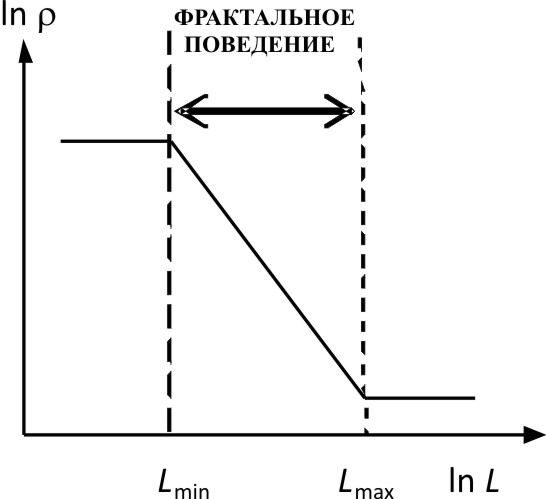
В отличие от математических фракталов, реальные фракталы (в том числе и полимеры) имеют два естественных масштаба длины   и   [рис. 1.5], выше и ниже которых объект фракталом не является [27]. Нижний предел L_min связан с конечным размером структурных элементов, а верхний L_max - со стремлением d_f к пределу [29]. Для полимеров экспериментально установлено [44; 55; 56], что L_min имеет порядок нескольких ангстрем, а L_max - нескольких десятков ангстрем. Отметим, что это совпадает с интервалом существования кластерной модели, где нижним пределом является размер (длина) статистического сегмента l_ст, а верхним - расстояние между кластерами R_кл [9].

Во-вторых, известно, что полимеры обладают многоуровневой структурой (молекулярный, топологический, надмолекулярный флокулярный или блочный уровни), элементы которой взаимосвязаны [9; 51; 57]. Кроме того, в результате воздействия на полимер могут быть образованы новые (вторичные) структурные элементы - трещины, поверхности разрушения, зоны пластической деформации и т.д. Указанные первичные и вторичные структурные элементы, а также формирующие их процессы характеризуются разнородными параметрами, поэтому до сих пор между ними были получены в лучшем случае только эмпирические корреляции. Если каждый из указанных элементов (процессов) охарактеризовать однородным параметром (например, фрактальной размерностью), то можно получить связывающие их аналитические соотношения, не содержащие подгоночных параметров. Это очень важно для компьютерного синтеза структуры и прогнозирования свойств и поведения высокомолекулярных соединений в процессе эксплуатации. Примеры такого прогнозирования в настоящее время уже получены [58-60].

В-третьих, для корректного использования указанных методов необходимо применение физически обоснованного числа параметров, описывающих структуру полимеров. В этом смысле евклидовы и фрактальные объекты принципиально различаются: первым требуется только одна размерность пространства (евклидова), а фрактальным объектам (пространствам) - не менее трех размерностей [33].