Научная электронная библиотека

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

1.3. Методы расчета фрактальных характеристик

Для количественной характеризации структуры полимеров в рамках фрактальных подходов необходимо уметь рассчитывать ее фрактальные характеристики (размерности). Наиболее простым методом расчета фрактальной размерности d_f структуры твердофазных полимеров является применение уравнения [29]:

d_f = (d - 1) (1+v_p), (1.14)

где v_р - коэффициент Пуассона, величину которого можно рассчитать по результатам механических испытаний с помощью соотношения [37]:

, (1.15)

где σ_Т - предел текучести, Е - модуль упругости.

Этот метод особенно удобен при оценке динамической фрактальной размерности, например, в ударных испытаниях полимеров [61].

Тот факт, что полимеры являются специфическими веществами, состоящими из длинных цепных макромолекул, делает гибкость полимерной цепи одной из наиболее важных характеристик полимеров. Авторы [30] получили следующее соотношение между С_∞ и d_f:

, (1.16)

которое подтверждено большим набором экспериментальных данных для разных полимеров [62].

Между двумя основными структурными концепциями, используемыми в настоящей монографии, существует тесная взаимосвязь, количественно выражаемая следующими уравнениями [9]:

(1.17)

или

, (1.18)

которые для наиболее часто используемого случая d = 3 приводятся к простому виду [9]:

, (1.19)

. (1.20)

Отметим, что указанные уравнения пригодны и для определения динамической фрактальной размерности, поскольку в силу термодинамической неравновесности структуры полимеров ее параметр порядка φ_кл является функцией временного масштаба эксперимента t. Величина φ_кл(t) в общем случае определяется так [63]:

, (1.21)

где - величина φ_кл при очень больших t, Τ₀ - время релаксации.

В свою очередь, в рамках перколяционных моделей величина φ_кл определяется следующим образом [24]:

φ_кл = 0,03(Т_с - Т)^0,55 (1.22)

для аморфных стеклообразных и

φ_кл = 0,03(1 - К)(Т_пл - Т)^0,55 (1.23)

для аморфно-кристаллических полимеров.

В уравнениях (1.22) и (1.23) Т_пл и Т - температуры плавления и испытаний, соответственно.

Экспериментальное определение величины d_f часто выполняется с помощью малоуглового рассеяния рентгеновских лучей (МУРР) [64]. В работах [65-68] такие измерения были сделаны для трех аморфных стеклообразных полимеров: полистирола (ПС), полиметилметакрилата (ПММА) и ПК. Для МУРР характерна степенная зависимость интенсивности рассеяния I от вектора рассеяния k = 4Πλ^-1sin(θ/2) (λ - длина волны, θ - угол рассеяния) [64]:

I(k) ~ k^-x, (1.24)

где х - показатель Порода. Для объемных фракталов (типа структуры полимеров) этот показатель совпадает с фрактальной размерностью структуры d_f(2 ≤d_f< 3) [64]. На рис. 1.6 приведена зависимость I(k) в двойных логарифмических координатах, а на рис. 1.7 - зависимость lnI от k², по которой можно определить радиус Гинье R. Для интерпретации этих результатов, обратимся к представлениям кластерной модели (см. раздел 1.1), для которой величина R будет равна двум расстояниям между кластерами R_кл.

В табл. 1.2 приведены значения R_кл и R, рассчитанных по наклону двух линейных участков зависимостей рис. 1.7. Обращает на себя внимание как близость абсолютных величин R_кл и R, так и двухкратное увеличение R при переходе от одного линейного участка зависимости lnI(k²) к другому, соответствующее переходу от R_кл к 2R_кл (рис. 1.7). Это позволяет предположить, что величины R и R_кл отражают один и тот же структурный элемент [67].

Наличие двух величин R предполагает существование границы между фрактальными структурными областями, оцениваемой из условий Rk = 1 [64]. Так, для фрактального кластера с размером 2R_кл = 70 Å получим lnk = - 4,25, что дает верхний линейный масштаб фрактального поведения структуры полимера. При R = R_кл = 35 Å получим lnk = - 3,56, что хорошо согласуется с величиной lnk, при которой происходит изменение наклона графиков рис. 1.6.

Таблица 1.2

Характеристики структуры аморфных стеклообразных полимеров, полученные методом МУРР [68]

Полимер	R_кл,Å	R, Å lnk < -3,56	R, Å lnk >-3,56		d_f		D_f
ПС	41	100	50	2,80	2,75	5,12	5,0
ПММА	37	100	50	2,80	2,70	5,20	4,33
ПК	30	80	40	2,40	2,62	4,40	3,63

Флуктуационный свободный объем аморфного полимера является фрактальным объектом, размерность которого совпадает с размерностью областей локализации избыточной энергии D_f, характеризующей степень энергетической возбужденности рыхлоупакованной матрицы [69; 70]. Величина D_f может быть определена из следующего соотношения [29]:

. (1.25)

По наклону прямых lnI - lnk в интервале lnk = - 4,25 ÷ - 3,56 была оценена величина х = в соответствии с уравнением (1.24). Из данных табл. 1.2. следует, что практически совпадает со значением d_f, определенным согласно уравнению (1.14), что подтверждает корректность предложенной трактовки [66].

Для фрактальной межфазной границы с размерностью D > 2 справедливо соотношение [71]:

I(k) ~ k^D-6, D < 6. (1.26)

Сравнение величин , полученных согласно уравнению (1.26) и D_f, рассчитанных по уравнению [1.25], показало их хорошее соответствие [табл. 1.2]. Таким образом, результаты измерения фрактальных размерностей структуры аморфных размерностей структуры аморфных полимеров методом МУРР находятся в хорошем согласии с данными, полученными другими независимыми способами [65-68].

Авторы [72] использовали представление структуры аморфного стеклообразного полимера (ПК) как кластера Виттена-Сандера (кластера WS), полученного диффузионно-ограниченной агрегацией (ДOA) [73; 74]. Такое представление позволяет использовать метод автокорреляционной функции [75] для оценки фрактальной размерности d_f структуры полимера. Как было показано в работе [75], автокорреляционная функция

C(r) = , (1.27)

где р(r') и р(r' + r) - вероятности того, что в точках r' и r' + r находится частица, из которых строится кластер (вероятность равна 1 при наличии и 0 - при отсутствии частицы), может быть представлена скейлинговым соотношением:

С(r) ~ r^-^α, (1.28)

для расстояний r, больших нескольких шагов решетки. В соотношении (1.28) величина α определяется разностью евклидовой размерности объемлющего пространства d и фрактальной размерности объекта (кластера) D [76]:

α = d - D. (1.29)

Следовательно, определив наклон α для линейной автокорреляционной функции, можно оценить фрактальную размерность объекта D, используя соотношения [1.28] и [1.29].

Как известно [77], модель Виттена-Сандера в своем первоначальном варианте [75] практически непригодна для описания реальных физических объектов, вследствие чего было разработано большое число ее модификаций. В частности, для описания структуры полимеров больше подходит модификация Виттена-Микина [77], суть которой заключается в следующем. В первоначальной модели [75] частицы, совершающие броуновское движение, присоединяются к неподвижной частице («затравке»), формируя в конечном итоге кластер. В модификации [77] использована не единственная «затравка», а большое их число. Очевидно, что радиус кластера WS не может превышать верхнего масштаба фрактального поведения структуры, т.е., несколько десятков ангстрем, как указано выше. Отсюда следует, что макроскопический полимерный образец должен состоять из большого числа таких кластеров WS, а это подразумевает такое же большое количество «затравок» [32].

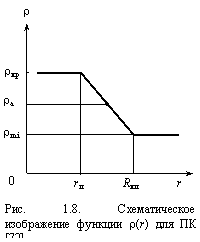
Схематическое представление автокорреляционной функции для аморфного полимера показано на рис. 1.8, где изменение плотности ρ дано как функция расстояния r, а начало отсчета (r = 0) помещено в центре области локального порядка. На некотором интервале от 0 до r_л(где r_л - радиус области локального порядка) величина ρ постоянна и равна плотности области локального порядка, которая в первом приближении принята равной соответствующей величине ρ_кр для кристаллического ПК [78]. Затем от r_лдо R_клпредполагается линейное снижение ρ до некоторой величины ρ_min, оцененной следующим образом [72]. В работе [78] приведена средняя величина плотности аморфного ПК ρ_а, которая на графике рис. 1.8 соответствует середине наклонного линейного участка зависимости ρ(r). Тогда из простых геометрических соображений получим [72]:

ρ_min= ρ_a - (ρ_кр - ρ_а). (1.30)

Далее можно оценить величину α из следующего соотношения [72]:

(ρ_кр - ρ_min) ~ (R_кл - r_л)^-^α, (1.31)

а затем рассчитать величину d_f из уравнения (1.29), поскольку для моделирования структуры полимера кластером WS выполняется условие [74]:

d_f = D. (1.32)

Величина r_л может быть рассчитана из простой геометрической схемы и соотношения [72]:

, (1.33)

где η - плотность упаковки, принимаемая равной 0,868 [79].

Сравнение полученных по уравнению (1.14) экспериментальных и рассчитанных в рамках модели WS ( , уравнения (1.29) и (1.31)) величин фрактальной размерности структуры ПК как функции температуры испытаний приведено на рис. 1.9. Как можно видеть, получено достаточно хорошее соответствие (расхождение в пределах 10 %). Однако, его можно улучшить использованием в уравнении (1.15) истинного, а не номинального, значения предела текучести , определяемого так [37]:

= σ_Т(1 + ε_Т), (1.34)

где ε_Т - деформация текучести.

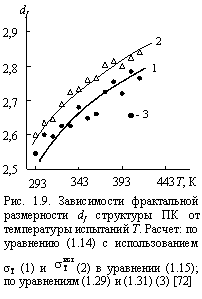
Как можно видеть [рис. 1.9], это уточнение дает еще лучшее соответствие величин и для ПК [72].

Как известно [24; 25], структура аморфных стеклообразных полимеров в рамках кластерной модели может моделироваться в рамках теории перколяции, а перколяционный кластер у порога протекания является фракталом [80]. Это позволяет определить величину d_f по критическим индексам перколяции β и ν, исходя из уравнения [80].

. (1.35)

Кроме того, в работе [79] были получены соотношения между критическими индексами перколяции β, ν и t и фрактальной размерностью перколяционного кластера d_f:

, (1.36)

, (1.37)

. (1.38)

Оцененные из этих соотношений значения критических индексов попадают в допустимые интервалы их изменения (β = 0,30 ÷ 0,40; ν = 0,8 ÷ 0,9; t = 1,6 ÷ 1,8), найденные для трехмерных перколяционных систем [80; 81]. Существенно, что получено совпадение не только числовых, но и смысловых значений этих величин [82].

Для аморфно-кристаллических полимеров величина d_f может быть оценена из уравнения [83]:

d_f = 2 + K. (1.39)

Авторы [84] использовали для оценки d_f ряда полиэтиленов данные по газопроницаемости этих аморфно-кристаллических полимеров. В работах [85; 86] предложено фрактальное соотношение для описания газопроницаемости полимеров:

, (1.40)

где Р - коэффициент газопроницаемости, Р₀ - константа, f_c - относительный флуктуационный свободный объем, d_h - диаметр микрополости этого объема, d_м - диаметр молекулы газа-диффузанта.

Поскольку для одного и того же полимера параметры Р₀, f_c и d_h являются константами, то зависимость Р(1/d_м) в двойных логарифмических координатах должна дать прямую с наклоном 2(D_f - d_s)/d_s. На рис. 1.10 приведены такие зависимости для четырех полиэтиленов, которые хорошо аппроксимируются прямыми, что позволяет определить их наклон Δ_н. Величина Δ_н равна ~ 3,5 для разветвленных ПЭНП и ПЭСП и ~ 5,0 и 7,5 для линейных ПЭВП + Z (Z - высокодисперсная смесь Fe/Fe), добавляемая в количестве 0,05 вес. %) и ПЭВП, соответственно. Поскольку процессы газопереноса в полимерах реализуются на масштабах порядка размера макромолекулярного клубка, то величина d_s была принята равной соответствующей размерности полимерной цепи, т.е., d_s = 1,0 для линейных и d_s = 1,33 для разветвленных полиэтиленов [49]. Это означает, что величина D_f ) в уравнении [1.40] варьируется в пределах ~ 3,66 ÷ 4,70.

Следовательно, в качестве размерности, контролирующей процессы газопереноса в полиэтиленах, нельзя принять размерность d_f, поскольку ее допустимая вариация составляет 2 ≤ d_f < 3 [26]. Однако, известно [47], что распределение размеров микрополостей свободного объема определяется величиной D_f, теоретическое значение которой может быть рассчитано из уравнения (1.25).

Сравнение величин и для ПЭНП, ПЭВП и ПЭВП + Z приведено в табл. 1.3, из которой следует достаточно хорошее соответствие этих размерностей.

Величины d_f и D_f связаны между собой соотношением (для d = 3) [29]:

. (1.41)

Таблица 1.3

Фрактальные размерности полиэтиленов [84]

Полимер	К	, ур-е [1.24]	, ур-е [1.39]	, ур-е [1.41]	, ур-е [1.40]	, ур-е [1.25]
ПЭНП	0,510	2,50	2,510	2,586	3,0	3,39
ПЭСП	0,638	-	2,638	2,624	3,76	-
ПЭВП	0,764	2,683	2,764	2,728	4,16	4,70
ПЭВП+Z	0,665	2,706	2,665	2,612	4,40	4,62

Уравнение [1.41] позволяет рассчитать величины d_f из полученных согласно данным рис. 1.10 значениям D_f. Эти значения d_f приведены в табл. 1.3 и сравнение их с оцененными согласно уравнениям [1.14] и [1.39] величинами и , соответственно, демонстрирует хорошее соответствие (расхождение не превышает 4 %) фрактальных размерностей структуры полиэтиленов, оцененных тремя указанными выше способами [84].

В работе [87] для прогнозирования фрактальной размерности d_f структуры сетчатых полимеров была использована модель конкурирующих процессов роста и зарождения упорядоченных областей [88]. Применение указанной модели позволило получить следующее уравнение [87]:

, (1.42)

где f - функциональность узлов химической сшивки; ν_с - плотность сшивки, а эмпирический числовой коэффициент в правой части уравнения получен приравниванием рассчитанных из уравнений (1.14) и [1.42] величин d_f при v_с = 10²⁷ м^-3 [87].

Далее рассмотрим методы определения фрактальной размерности D_f макромолекулярного клубка в полимерном расплаве. В этом случае предполагается (и на практике это наблюдается достаточно часто), что температура испытаний Т превышает температуру так называемого перехода «жидкость 1 - жидкость 2» T_ll, величину которой можно определить так [11]:

T_ll = (1,20 ± 0,05)T_c. (1.43)

При T = T_ll происходит переход полимерного расплава от «жидкости с фиксированной структурой» (где наблюдается остаточная структурная упорядоченность [11]) к истинно жидкому состоянию или «бесструктурной жидкости». Тем не менее, «бесструктурность» расплава относится к отсутствию надмолекулярной структуры, но структура макромолекулярного клубка в расплаве остается важным структурным фактором (по существу, единственным при T > T_ll) [89].

Наиболее точно структуру макромолекулярного клубка, который является фрактальным объектом [36], можно охарактеризовать с помощью его фрактальной (Хаусдорфовой) размерности D_f, описывающей распределение элементов клубка в пространстве [26]. Величину D_f макромолекулярного клубка в расплаве можно определить из уравнения [36]:

, (1.44)

где d_s - спектральная размерность клубка [49].

Величина d_s связана с фрактальной размерностью D макромолекулярного клубка в растворе следующим соотношением [36]:

. (1.45)

В свою очередь, величину D можно определить по значению показателя а в уравнении Марка-Куна-Хаувинка [90]:

. (1.46)

Сочетание уравнений (1.44) ÷ (1.46) позволяет рассчитать величины D_f, исходя из известных значений а [89]. Оценку величины D_f можно выполнить также следующим образом [91]. Формальная кинетика химических реакций может быть описана уравнением:

, (1.47)

где Q -степень завершенности реакции, t - ее продолжительность, k_d - константа скорости реакции.

Общее фрактальное соотношение, также используемое для описания кинетики химических реакций, имеет вид [34]:

. (1.48)

Дифференцируя соотношение (1.48) по времени t и приравнивая производную dQ/dt к аналогичной производной в уравнении (1.47), получим [91]:

, (1.49)

где С₁ - константа, которую можно оценить из граничных условий.

Известно [92; 93], что получение полимерных изделий из разных растворителей приводит к существенной вариации их структуры и свойств. Предполагается, что этот эффект существенно зависит от природы растворителя, поскольку концентрированные растворы полимеров уже содержат структуры, схожие с простыми типами структур конденсированного состояния полимеров [93].

Аналитически эта взаимосвязь описана в рамках фрактального анализа, где было получено простое соотношение между фрактальными размерностями структуры макромолекулярного клубка в растворе D и структуры конденсированного состояния (расплава) полимеров D_f, которое для линейных полимеров имеет вид [94; 95]:

D_f = 1,5D, (1.50)

а для разветвленных:

D_f = 1,67D. (1.51)

Таким образом, в качестве первой стадии определения величины D_fдля полученных из разных растворителей полимеров следует рассматривать прогнозирование величины D, характеризующей структуру макромолекулярного клубка в растворе [36]. Для этого существует достаточно большое число методов, поскольку, как и следовало ожидать, структура клубка определяет свойства растворов и, следовательно, величины их основных традиционных характеристик.

Авторы [96] получили следующую взаимосвязь между D, молекулярной массой полимера М и постоянной Хаггинса k_x, характеризующей степень взаимодействия полимер - растворитель:

, (1.52)

где K_h - константа в уравнении Марка-Куна-Хаувинка.

Зависимость D от молекулярных характеристик полимера С_¥ и S предложена в [97]:

. (1.53)

Известно [35], что величина D определяется двумя группами взаимодействий: взаимодействиями полимер - растворитель и взаимодействиями элементов клубка между собой. Такое определение позволило связать D и параметр взаимодействия Флори-Хаггинса c₁, который определяется следующим образом [21]:

, (1.54)

где Е_исп - мольная энергия испарения растворителя, R - универсальная газовая постоянная, d_п и d_р - параметры растворимости полимера и растворителя, соответственно, c_S - эмпирический параметр, называемый иногда энтропийной составляющей параметра Флори-Хаггинса [21].

Набор экспериментальных данных для разных полимеров позволил получить эмпирическую корреляцию D(c₁) следующего вида [98]:

D = 1,50 + 0,45c₁. (1.55)

Используя двухкомпонентную модель параметра растворимости [99], авторы [100] получили следующую формулу для определения D:

, (1.56)

где компонента d_fs параметра растворимости включает энергию дисперсионных взаимодействий и энергию взаимодействия дипольных связей, а компонента d_с - энергию взаимодействия водородных связей и энергию взаимодействия между атомом с недостатком электронов одной молекулы (акцептором) и атомом с избытком электронов другой молекулы (донором), которая требует определенной ориентации этих двух молекул. В такой трактовке нет необходимости вводить отдельную компоненту для описания взаимодействий между полярными молекулами [99]. В уравнении (1.56) величина Dd_fs представляет собой разность компонент d_fs полимера и растворителя, а d_с - соответствующую компоненту для растворителя [100].

Авторы [101, 102] предложили методику оценки D, основанную на измерении вязкостных характеристик полимерных растворов:

, (1.57)

где [h] и [h]_q - характеристические вязкости полимера в произвольном и q-растворителях, соответственно.

Взаимосвязь величины D и длины сегмента Куна А, характеризующей жесткость полимерной цепи, рассмотрена в работе [103]. Для гибкоцепных полимеров получено уравнение:

D = 2,0 - 1,32 ´ 10^-2 A, (1.58)

а для жесткоцепных:

D = 1,667 - 4,45 ´ 10^-4 A, (1.59)

где величина А дается в ангстремах (Å) [103].

И, наконец, для разветвленных полимеров авторы [104; 105] получили следующее уравнение:

, (1.60)

где [h]_p и [h]_л - характеристические вязкости разветвленного полимера и его линейного аналога, соответственно, а фактор разветвленности g определяется так [106]:

. (1.61)

Для оценки D может быть использовано следующее уравнение [36]:

, (1.62)

где d_f - фрактальная размерность растворителя, D_ph - фантомная (не учитывающая взаимодействий исключенного объема) размерность макромолекулярного клубка.

Величина D_ph дается следующим образом [36]:

, (1.63)