Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОСНОВЫ КОНСТРУИРОВАНИЯ И ТЕХНОЛОГИИ ПРОИЗВОДСТВА РЭС

Евстафьев В. В., Енгибарян И. А., Сахаров И. А.,

1.2. Математические модели проектируемых объектов

Компьютерное моделирование можно рассматривать как один из самых мощных методов и инструментов познания, анализа и синтеза, которым располагают проектировщики. Идея компьютерного моделирования состоит в замене реального объекта его образом в виде математической модели, разработки соответствующей программы для ЭВМ и проведения машинных экспериментов с целью получения новых знаний о проектируемом объекте. При этом экспериментировать с моделью объекта возможно даже тогда, когда на реальном объекте нецелесообразно и даже практически невозможно. Работа не с самим объектом или процессом, а с его математической моделью дает возможность относительно быстро и без существенных затрат исследовать его свойства и поведение в любых возможных ситуациях.

Понятие математической модели не имеет строгого формального определения. Обычно под математической моделью объекта понимают совокупность отношений выраженных при помощи системы математических символов и обозначений, которые отражают наиболее существенные свойства исследуемого объекта.

Процедуру построения модели принято называть идентификацией, при этом данный термин относится к построению аналитических математических моделей динамических объектов. Динамический объект – это объект, выход которого зависит не только от текущего значения входных сигналов, но и от их значений в предыдущие моменты времени. В этом случае идентифицированный объект принято представлять в виде, показанном на рис. 1.2.1, где t – время; u(t) – контролируемый (иногда управляемый) входной сигнал; y′(t) – теоретический выход объекта; y(t) – наблюдаемый выход объекта; e(t) – случайная аддитивная помеха, отражающая действие неучитываемых факторов (шум наблюдения).

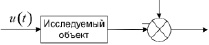
Рис. 1.2.1. Общее представление идентифицируемого объекта

Обычно предполагают, что связь между входным и «теоретическим» выходным сигналами задается в виде некоторого оператора ψ:

y′(t) = ψ[u(t)], (1.1)

при этом наблюдаемый выход объекта может быть описан соотношением:

y(t) = ψ[u(t)] + e(t). (1.2)

Принцип суперпозиции позволяет объединить все действующие помехи в одну общую e(t) и приложить её к линейной модели. При рассмотрении задач идентификации все помехи считают независимыми.

Цель идентификации заключается в том, что на основании наблюдений за входным u(t) и выходным y(t) сигналами на каком-то интервале времени определить вид оператора, связывающего входной и теоретический выходной сигналы.

Перед началом экспериментальных исследований проводят априорный анализ перечня входных переменных с целью отбора и включения в состав модели приоритетных, оказывающих наиболее сильное воздействие на выходные переменные y(t). В первую очередь в их
состав включают управляющие входные переменные, с помощью которых осуществляется регулирующее воздействие на исследуемый объект.

Понятие «оценка модели исследуемого объекта» означает, что в процессе математической обработки массива данных при необходимости можно менять структуру моделей, например вместо линейной модели можно использовать нелинейные различных типов.

Если структура не меняется, производятся только оценки параметров модели. Известны два принципиально различающихся подхода к получению оценки моделей (1.1) или (1.2):

а) экспериментально-статистический – модель представляют в виде формального уравнения (системы уравнений), связывающего входные и выходные переменные в определенном (обычно относительно небольшом) диапазоне изменения переменных;

б) аналитический – модель выводится из физических представлений о сути процессов в исследуемом объекте.

Рассмотрим основные виды моделей линейных непрерывных стационарных динамических объектов и их взаимосвязь (действием шума e(t) пока пренебрегаем).

Дифференциальное уравнение. Наиболее универсальная модель, имеющая форму:

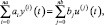(1.3)

где na – порядок модели (na > nb); ai и bj – постоянные коэффициенты (параметры модели); u(j)(t) и y(j)(t) – производные, соответственно, входного и выходного сигналов.

Передаточная функция. Данная характеристика определяется как отношение преобразования Лапласа выходного и входного сигналов

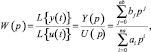(1.4)

где L{} – символ преобразования Лапласа; р – комплексная переменная (оператор Лапласа).

Импульсная характеристика ω(t). Под импульсной характеристикой понимается реакция предварительно невозмущенного объекта (т.е. объекта с нулевыми начальными условиями) на входной сигнал в виде дельта-функции.

Переходная функция h(t). Это реакция предварительно невозмущенного объекта на входной сигнал в виде единичного скачка (единичной ступенчатой функции). Из теории автоматического управления известно:

L{ω(t)} = W(p); ω(t) = h′(t); 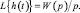(1.5)

При нулевых начальных условиях связь между выходными и входными сигналами описывается интегралом свертки:

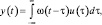(1.6)

или в операторной форме:

Y(p) = W(p)∙U(p). (1.7)

Частотные характеристики. Частотные характеристики объекта определяются его комплексным коэффициентом передачи при подстановке вместо оператора Лапласа p комплексного аргумента jω, который является Фурье – преобразованием импульсной характеристики.

Модуль комплексного коэффициента передачи:

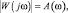(1.8)

представляет собой амплитудно-частотную характеристику (АЧХ) объекта с передаточной функцией W(p), а аргумент

arg(W(jω)) = φ(ω), (1.9)

является фазо-частотной характеристикой (ФЧХ).

Графическое представление W(jω), на комплексной плоскости при изменении ω0 ≤ 0 до ∞, т.е. график амплитудно-фазовой характеристики (АФЧ) в полярных координатах в отечественной литературе называется годографом, а в англоязычной – диаграммой Найквиста. На практике часто используется логарифмическая амплитудно – частотная характеристика (ЛАЧХ), равная .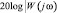

Модель для переменных состояний. В 70-е годы прошлого столетия Г. Розенброком был создан метод «размытых» частотных характеристик, предназначенный для автоматизированного проектирования систем с несколькими входами и выходами, ориентированный на использование средств вычислительной техники и названной метод переменных состояния (МПС).

В основе этого метода лежит представление дифференциальных уравнений в нормальной форме Коши, который дополняется алгебраическими уравнениями, связывающими выходные переменные с переменными состояния

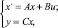(1.10)

где u – вектор входных воздействий; у – вектор выходных воздействий; х – вектор переменных состояния; А, В, С – матрицы коэффициентами размерности (nхn), (nxm), (rxn) соответственно; n – число переменных состояния или максимальная степень производного исходного уравнения; m – число входов; r – число выходов.

Математическим аппаратом МПС являются матричное исчисление и вычислительные методы линейной алгебры.

Следует отметить, что все приведенные модели являются эквивалентными, т.е., зная любую из них, можно получить все остальные.

На практике в большинстве случаев измерение непрерывных сигналов производится в дискретные моменты времени tk = kT, где Т – интервал дискретизации. Такое представление данных обеспечивает определенное удобство при последующей обработке их на ЭВМ. Поэтому использование дискретных моделей в место непрерывных является актуальной задачей.

В дискретных моделях аналогом дифференциального уравнения является разностное уравнение

yk + a1yk–1 + ...+ anayk–na = b1uk + b2uk–1 + b3uk–2 + ...+ bnbuk–nb+1, (1.11)

где

yk–i = y[(k – i)T]; uk–j = u[(k – j)T].

Связь между сигналами может быть отражена;

б) через дискретную свертку

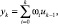(1.12)

где ω – ордината решетчатой весовой функции объекта, с использованием аппарата Z-преобразования:

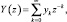(1.13)

где z = epT.

в) через дискретную передаточную функцию:

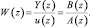(1.14)

Множитель z–1 = e–pT представляет собой оператор задержки.