Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОСНОВЫ КОНСТРУИРОВАНИЯ И ТЕХНОЛОГИИ ПРОИЗВОДСТВА РЭС

Евстафьев В. В., Енгибарян И. А., Сахаров И. А.,

1.3. Общая характеристика приложения MATLAB пакета System Identification Toolbox

Пакет System Identification Toolbox содержит средства для создания математических моделей линейных динамических объектов на основе наблюдаемых входных/выходных данных. Методы идентификации входящие в пакет применимы для решения широкого класса задач. Графический интерфейс пакета упрощает как предварительную обработку данных, так и диалоговый процесс идентификации модели. Операции загрузки и сохранения данных, выбора их диапазона, исключения смещений и трендов выполняются минимальными усилиями и доступны из главного меню. Представление данных и моделей систем и объектов организовано таким образом, что в процессе интерактивной идентификации пользователь легко может вернуться к предыдущему этапу работы.

Для начинающих пользователей существует возможность просматривать предыдущие и последующие этапы. Специалисту графические средства позволяют отыскать любую из ранее полученных моделей и оценить ее качество с другими моделями.

Пакет поддерживает все традиционные виды моделей, включая модели передаточных функций, описания для переменных состояния (как для непрерывного, так и для дискретного времени) и другие с произвольным числом входов и выходов.

Рассмотрим несколько распространенных моделей дискретных объектов, используемых в пакете System Identification Toolbox для временной области, учитывающих действие шума наблюдения.

1. Модель авторегрессии AR (AutoRegressive) – считается самым простым описанием:

A(z)∙y(t) = e(t), (1.15)

где A(z) = 1 + a1z–1 + a2z–2 +...+ anaz–na; e(t) – дискретный белый шум.

2. ARX-модель (Autoregressive with externat input) – более сложная модель:

A(z)y(t) = B(z)u(t) + e(t); (1.16)

B(z) = b1 + b2z–1 +...+ bnbz–nb+1,

или в раъзвернутом виде:

y(t) + a1y(t – 1) + ...+ anay(t – na) = b1u(t) + b2u(t – 1) + ...+
+ bnbu(t – nb + 1) + e(t).

3. ARMAX – модель (AutoRegressive-Moving Average with external input – модель авторегрессии скользящего среднего):

A(z)y(t) = B(z)u(t – nk) + C(z)e(t);

C(z) = 1 + c1z–1 + c2z–2 +...+ cncz–nc, (1.17)

где nk – величина задержки (запаздывания).

4. Модель «вход-выход» («Output – Error», т.е. «выход – ошибка» сокращенно ОЕ):

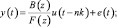(1.18)

F(z) = 1 + f1z–1 + f2z–2 +...+ fnfz–nf.

5. Модель Бокса-Дженкинса(BJ):

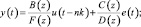(1.19)

D(z) = 1 + d1z–1 + d2z–2 +...+ dndz–nd.

Все предыдущие пять моделей можно рассматривать, как частные случаи обобщенной параметрической линейной структуры:

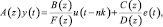(1.20)

при этом все они допускают расширение для многомерных объектов (имеющих несколько входов и выходов).

6. Модель для переменных состояния (State – space):

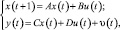(1.21)

где A, B, C, D – матрицы соответствующих размеров; υ(t) – коррелированный белый шум наблюдений.

Следует обратить внимание, что в своей работе пакет System Identification Toolbox использует три внутренних вида матричного представления моделей, которые с помощью операторов и функций пакета преобразуется во все выше перечисленные виды моделей объектов:

а) для временных моделей – тета-формат;

б) для частотных моделей – частотный формат;

в) формат нулей и полюсов.