Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

2.2. Мультифрактальные модели процессов газопереноса в полимерах

Как отмечалось выше, величина D для ПЭ скачкообразно изменяется при Т_пл [9]. Этот эффект получил объяснение с позиций разных теоретических концепций, цитированных выше [9; 11; 26]. Однако существует еще один фундаментальный структурный аспект проблемы, которому до сих пор не уделялось должного внимания. Наличие этого аспекта вытекает из двух хорошо известных экспериментальных наблюдений: зависимости D(d_м), описанной выше, и резко различающейся степени этой зависимости для аморфно-кристаллического ПЭВП и его расплава [9]. В последнем случае зависимость D(d_м) выражена гораздо слабее, чем в первом. Эти наблюдения позволяют сделать следующее предположение. В аморфно-кристаллическом ПЭВП существует типичное для полимеров распределение размеров микрополостей свободного объема d_h. Такое распределение (или мультифрактальность) микрополостей свободного объема является следствием мультифрактальности структуры полимера [36; 53]. Если исходить из приближенного условия реализации диффузии d_м £ d_h, то это означает, что по мере роста d_м в аморфно-кристаллическом полимере остается все меньше микрополостей с размером d_h, соответствующих условию реализации диффузии, и это резко снижает величину D. Расплав полиэтилена является евклидовым объектом [8], для которого характерно монодисперсное распределение d_h и это нивелирует различия в диффузии молекул газов-диффузантов с разными d_h. Один из авторов настоящей монографии выполнил проверку корректности сделанного выше предположения на примере диффузии разных газов через аморфно-кристаллический ПЭВП и его расплав [54; 55].

Для определения коэффициента диффузии D использовано уравнение [9]:

D = D₀exp(-E_акт/RT),                                         (2.21)

где D₀ - константа для каждого газа-диффузант; Е_акт - энергия активации процесса диффузии; R - универсальная газовая постоянная.

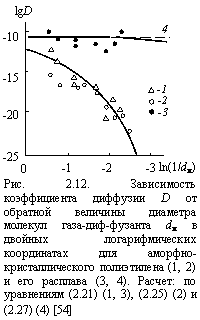
На рис. 2.12 показана зависимость D(1/d_м) для диффузии 9 газов [9] в случае аморфно-кристаллического полиэтилена и его расплава в двойных логарифмических координатах, где величина D определена согласно уравнению (2.21). Как можно видеть, эта зависимость резко различается для двух указанных состояний полимера: если для аморфно-кристаллического ПЭВП наблюдается сильный спад D по мере роста d_м, то для расплава эта зависимость практически отсутствует. Поскольку зависимость D(1/d_м) для аморфно-кристаллического полиэтилена криволинейна, то это означает изменение показателя 2(D_f - d_s)/d_s в уравнении (2.5) по мере вариации масштаба измерения d_м или, с учетом условия d_s = const, изменение размерности D_f. Из уравнения (1.41) следует, что изменение D_f с масштабом означает аналогичное изменение d_f. Аппроксимируя криволинейную зависимость D(1/d_м) прямолинейными отрезками, из их наклона можно рассчитать величину показателя 2(D_f - d_s)/d_s, затем размерность D_f и по уравнению (1.41) - величину d_f для каждого такого участка.

 

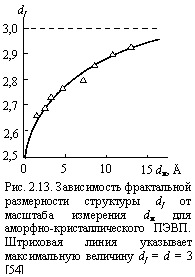
На рис. 2.13 показана зависимость d_f(d_м), из которой следует рост d_f по мере увеличения d_м или увеличения масштаба измерения. Это является типичным признаком мультифрактальности структуры аморфно-кристаллического полиэтилена [37]. Отметим, что исходя из данных рис. 2.12 и уравнения (1.41), аналогичную диаграмму можно построить и для D_f, что означает мультифрактальность свободного объема в аморфно-кристаллическом ПЭВП, которая является следствием мультифрактальности структуры этого полимера (рис. 2.13). Рис. 2.13 показывает снижение d_f по мере уменьшения масштаба d_м, т.е. увеличение плотности структуры с уменьшением масштаба [56]. Это по существу является определением фрактала по соотношению [42]:

,                                                            (2.22)

где r - плотность фрактального объекта; R_g - его радиус инерции.

Как известно [36], число микрополостей размером d_h можно оценить из соотношения:

.                                                         (2.23)

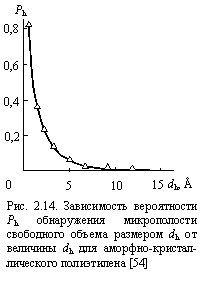
Если предположить, что N_h соответствует относительно доле микрополостей размером d_h, то можно (после соответствующей нормировки величин N_h) построить распределение d_h, показанное на рис. 2.14. Как следует из этого рисунка, вероятность P_h (равная относительной доле микрополостей с размером ³ d_h) обнаружения микрополости с размером больше d_h быстро снижается по мере роста d_h. Так, вероятность обнаружения микрополости с d_h » 12Å равна 0,001.

Теперь рассмотрим зависимость D(1/d_м) для расплава полиэтилена, также показанную на рис. 2.12. В первом приближении ее наклон равен нулю и это означает следующее условие:

2(D_f - d_s)/d_s = 0                                                  (2.24)

или

D_f = d_s.                                                                  (2.25)

Для полимерных цепей d_s £ 1,33 [32], а минимальная величина D_f для непористых мембран (n_р = 0) равняется 2 (уравнение (1.25)). Таким образом, нельзя получить условие (2.25) в предположении фрактальности расплава ПЭВП. Поэтому следует предположить, что расплав является евклидовым объектом, в котором размерность D_f теряет свой смысл. С формальной точки зрения это следует из уравнения (1.41): при d_f = d величина D_f ® ¥. Со структурных позиций это означает следующее: размерность D_f характеризует степень энергетической возбужденности рыхлоупакованных областей полимера. В расплаве отсутствуют и кристаллиты, и «замороженный» локальный порядок, вследствие чего нет необходимости отдельной характеризации разных структурных компонент и весь расплав характеризуется размерностью d = 3. Для евклидовых объектов справедливо тождество [57]:

d_s = d_f = d = 3.                                                     (2.26)

Поэтому условие (2.25) для евклидовых объектов выполняется тривиально при замене D_f на d_f = d.

Таким образом, исходя из вышесказанного, уравнение (2.5) в случае расплава принимает вид:

,                                                          (2.27)

где величину f_c можно принять согласно Бойеру [58] равной ~ 0,113. Следовательно, для расплава полиэтилена D с точностью до константы равен  и постоянен. Величина  в этом случае равна 2,45 ´ 10^-4 см²/с, что близко к теоретической величине  [9]:

 см²/с,                        (2.28)

рассчитываемой исходя из предположения о скачке молекулы газа-диффузанта на расстояние l в несколько ангстрем с частотой n = 10¹² ¸ 10¹³ Гц. Рассчитанная по уравнению (2.27) величина D при указанных выше значениях констант  и f_c показана на рис. 2.12 штриховой линией. Теоретический расчет хорошо согласуется с экспериментальной зависимостью и это означает отсутствие мультифрактальности (распределения) размеров микрополостей свободного объема в расплаве, что, как отмечалось выше, является следствием потери структурой полимера фрактальных свойств.

Зависимость рассчитанного по уравнению (2.5) параметра  для аморфно-кристаллического ПЭВП показана на рис. 2.15. Как следует из приведенных данных, наблюдаются большие значения  (порядка 10^-5 см²/с) только для двух инертных газов с наименьшим размером молекул (Не и Ne), а для остальных газов-диффузантов величина  примерно постоянна и имеет порядок 10^-7 см²/с. Это дает возможность теоретической оценки коэффициента диффузии D для аморфно-кристаллического ПЭВП при следующих условиях:  = 3,8 ´ 10^-7 см²/с, f_c = 0,07, d_s = 1,0 d_h = 6,18 Å и величины D_f принимались в интервале 4,06 ¸ 9,78 согласно их оценке из наклона линейной аппроксимации отдельных участков криволинейной зависимости D(1/d_м), рис. 2.12. Cравнение теории и эксперимента, показанное на рис. 2.12, продемонстрировало их хорошее соответствие, за исключением данных для Hе и Ne по указанной выше причине. Следовательно, соответствие теории и эксперимента для аморфно-кристаллического ПЭВП достигается при учете зависимости d_а (или D_f) от масштаба измерения d_м и включения в расчетную схему этих масштабов (d_м и d_п), что однозначно указывает на мультифрактальность структуры (и, следовательно, свободного объема) этого полимера. Для получения соответствия теории и эксперимента в случае расплава полиэтилена, который является евклидовым объектом, учет вышеуказанных условий не требуется [55].

Далее можно построить мультифрактальную диаграмму для структуры ПЭВП в терминах a - f, где a - скейлинговый показатель, характеризующий концентрацию сингулярностей, f - размерность сингулярностей a [59]. Для этой цели используем простейший вариант [60]:

,                                                                              (2.29)

где P_i - вероятность обнаружения микрополости с относительным размером l_i.

Величина P_i принята равной P_h (рис. 2.14), а l_i определена из построения множества («пыли») Кантора следующим образом. Из данных рис. 2.14 следует, что интервал вариации d_h можно принять равным 0 ¸ 12Å. Тогда величина d_м должна нормироваться на величину интервала вариации d_h, т.е., 12 Å. Далее в построении Кантора из первоначального отрезка длиной 1 удаляется средняя его часть (одна треть) и тогда длина двух оставшихся частей будет равна ~ 0,667 [59; 61]. Затем эту величину следует разделить пропорционально размеру между поверхностями соседних микрополостей и размеру микрополости свободного объема при условии d_h = d_м и последняя из указанных частей соответствует l_i [61; 62]. Величина f рассчитывается так [61]:

f = d_f - 2.                                                              (2.30)

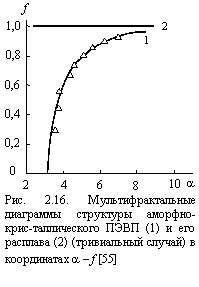
Построенная таким образом диаграмма a - f для аморфно-кристаллического ПЭВП показана на рис. 2.16, где также приведена диаграмма a - f для расплава полиэтилена (тривиальный случай), которая является прямой с ординатой f = 1 (d_f = d = 3), параллельной оси a. Диаграмма a - f для аморфно-кристаллического ПЭВП имеет куполообразную форму, типичную для таких диаграмм [59-62]. Ее физический смысл заключается в следующем: кривая a - f показывает вероятность обнаружения в полимере микрополости с размером больше произвольного d_h при произвольной d_f [54].

Таким образом, изложенные выше данные экспериментально подтверждают мультифрактальную природу структуры (и, как следствие, свободного объема) аморфно-кристаллического полиэтилена и дают оценку его мультифрактальных характеристик на основе диффузионных свойств этого полимера. Такой подход позволил также построить кривую распределения размеров микрополостей свободного объема. Диаграмма a - f в обычных (уже классических) координатах мультифрактального формализма показывает вероятность существования в полимере микрополостей с размером больше любого фиксированного их диаметра d_h. Расплав полиэтилена является евклидовым объектом с монодисперсным распределением размеров микрополостей. Указанные обстоятельства определяют разную форму зависимостей коэффициента диффузии D от размера молекул газа-диффузанта [54; 55].

Еще один вариант мультифрактальной (вероятностной) модели диффузии газов в полимерах предложен в работе [63]. Как известно [23], величину D для аморфно-кристаллических полимеров можно выразить следующим эмпирическим уравнением:

,                                                         (2.31)

где эмпирический показатель m может принимать разные значения (примерно от 0 до 1 [23]) и его физический смысл или связь со структурой полимера остаются неясными. Ранее величины D_a определялись экстраполяцией зависимости D(K) к К = 0. Мы полагаем, что такое определение D_a не корректно в силу указанного выше скачка D [9] при Т_пл ПЭВП, т.е., при переходе ПЭВП из твердофазного аморфно-кристаллического состояния в аморфный расплав. Поэтому в работе [63] величины D_a были определены по уравнению (2.21), причем значения D₀ и Е_акт соответствовали Т = 400 К. Кроме того, сделанный в работе [63] выбор в качестве объекта исследования одного полимера (ПЭВП) и семи газов-диффузантов позволяет установить, действительно ли показатель m связан со структурными характеристиками полимера или определяется другими факторами. Очевидно, что в первом случае должно выполняться условие m = const для всех семи газов, а во втором случае величина m будет переменной. Предварительные оценки согласно уравнению (2.31) показали, что величина m варьируется в широких пределах: примерно от 2 для Hе до 7 для С₄Н₁₀ и в первом приближении можно предположить m = d_м, где d_м дается в Å. Это обстоятельство позволяет записать уравнение (2.31) следующим образом [63]:

,                                                        (2.32)

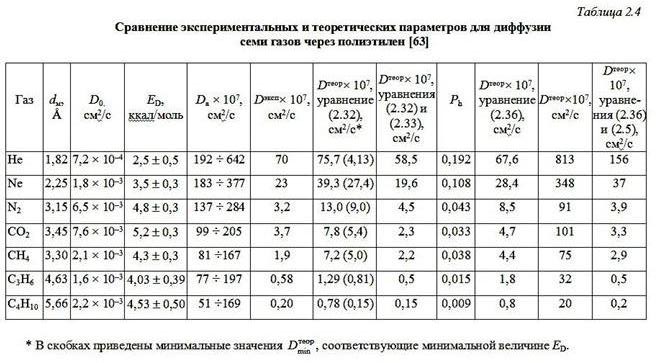
где j_а = 1 - K = 0,43 = const, и использовать его для расчета теоретических значений коэффициента диффузии D^теор. Приведенное в табл. 2.4 сравнение D^эксп и D^теор показало их хорошее соответствие, а значительный разброс величины Е_акт, увеличивающий вариацию расчета D_a в силу экспоненциальной формы уравнения (2.21), позволяет получить еще лучшее соответствие D^эксп и (табл. 2.4).

Это количественное соответствие можно улучшить следующим простым способом. Как известно [11; 64], непроницаемыми для диффузии газов в полиэтиленах являются не только кристаллические области, но и области локального порядка (кластеры). Тогда доля доступной для диффузии газов аморфной фазы определяется так [63]:

j_a = 1 - K - j_кл,                                                 (2.33)

а доля доступной для диффузии газа с диаметром молекулы d_м аморфной фазы дается как . В табл. 2.4 приведены результаты расчета D^теор указанным способом, позволившего получить лучшее соответствие теории и эксперимента.

Полученные результаты позволяют выяснить физический смысл показателя m в уравнении (2.31), предполагаемого равного d_м. Доступная для диффузии молекул газа-диффузанта с диаметром d_м доля аморфной фазы  определяется так [63]:

.                                                        (2.34)

 

Увеличение d_м приводит к снижению  за счет уменьшения числа микрополостей свободного объема с диаметром d_h ³ d_м, через которые реализуется диффузия и, как следствие, к уменьшению D. По своему физическому смыслу параметр  эквивалентен вероятности P_h обнаружения в полимере микрополости флуктуационного свободного объема с диаметром d_h при условии d_h ³ d_м [55]. Вероятность Р_h(d_м) может быть оценена следующим образом [55]:

P_h(d_м) = ,                                                    (2.35)

 где d_f для ПЭВП равна ~ 2,75 [27].

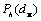На рис. 2.17 приведено сравнение трех зависимостей: ,  и . Как и следовало ожидать, для всех трех зависимостей наблюдается резкий спад аргумента по мере роста d_м, что обусловлено наличием распределения по размерам микрополостей свободного объема или мультифрактальностью структуры ПЭВП [54; 55]. В этом случае можно записать следующее уравнение для определения D^теор [63]:

D^теор = D_aP_h.                         (2.36)

Приведенное в табл. 2.4 сравнение величин D^эксп и D^теор, рассчитанных по уравнению (2.36), показало хорошее соответствие этих параметров.

В табл. 2.4 также приведены результаты расчета  для указанных семи газов согласно уравнению (2.5) (f_c = 0,113 [58], d_h = 12Å [43], d_f = D¢ = 2,95 [42] и d_s = 1,0 [32]) и сравнение их с D_a, рассчитанным по уравнению (2.21), которое показало хорошее соответствие. Кроме того, в этой же таблице даны значения D^теор, рассчитанные по уравнениям (2.5) и (2.36), которые также обнаружили хорошее соответствие с экспериментальными величинами коэффициента диффузии D^эксп.

Таким образом, данные работы [63] показали, что показатель m в уравнении (2.31), строго говоря, не связан со структурой полиэтилена, а зависит от размера молекул газа-диффузанта, определяющего долю доступной для диффузии этого газа аморфной фазы. По существу, это является проявлением мультифрактальности структуры полимера, которая выражается в зависимости его свойств от масштаба измерения, т.е., в данном случае - от диаметра молекулы газа-диффузанта [63].

Выше описано несколько фрактальных механизмов газопереноса в полимерных мембранах. Отметим, что они даны для переноса одних и тех же газов через один и тот же полимер (ПЭВП). Поэтому авторы [65] выполнили сравнение предложенных механизмов для нахождения их возможной общности на примере коэффициента разделения серии углеводородов С₁ - С₄ мембраной аморфно-кристаллического ПЭВП. Общее фрактальное уравнение для определения коэффициента разделения a_ik двух газов i и k полимерной мембраной имеет вид [65]:

.  (2.37)

Уравнение (2.37) описывает обе рассмотренные выше трактовки газопереноса при следующих условиях. Если рассматриваются структурный и молекулярный механизмы, то для первого из них принимается D_f = const и D¢ = d_f, а для второго - D_f = const и в числителе третьего сомножителя правой части уравнения (2.37) D¢ = d_f, а в знаменателе - D¢ = D_f. Если же рассматривается мультифрактальная трактовка, то D_f является переменной величиной, определяемой из мультифрактального спектра d_f(d_м) (рис. 2.13) с помощью уравнения (1.41), а D¢ = d_f.

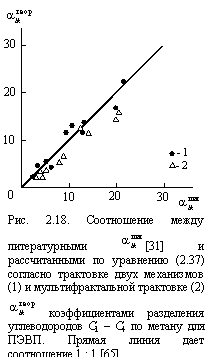
На рис. 2.18 приведено сравнение литературных [31] и рассчитанных по уравнению (2.37)  величин коэффициента разделения 11 углеводородов по метану (СН₄) для ПЭВП, где величины были определены согласно обеим рассмотренным выше трактовкам. Как можно видеть, между  и полученными обоими методами  наблюдается хорошее соответствие, которое предполагает определенную физическую общность обеих предложенных трактовок.

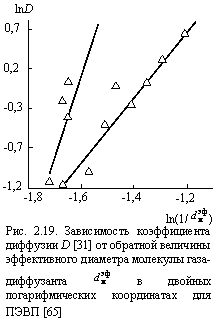
Рассмотрим физические основы предполагаемой общности трактовок. В рамках модели [26] структурный механизм для небольших  предполагает прямую диффузию молекул газа-диффузанта через микрополости флуктуационного свободного объема без заметного влияния стенок этих микрополостей, которые представляют собой поверхность колеблющихся вокруг положения равновесия сегментов макромолекул с размерностью, примерно равной D_f [45]. В этом случае диффузия газов контролируется структурой полимера, характеризуемой ее фрактальной размерностью d_f, по принципу: чем больше d_f, тем больше относительный флуктуационный свободный объем f_c и d_h и тем выше коэффициент диффузии D. При этом первый сомножитель в правой части уравнения (2.37) всегда включает в качестве показателя размерность D_f, поскольку он характеризует растворимость газа в полимере, которая по своей физической сущности является сорбцией молекул газа на поверхности микрополостей свободного объема [45; 46]. Для разветвленных (сшитых) полимеров увеличение спектральной размерности d_s по сравнению с линейными (от 1,0 до 1,33 [32]) приводит к снижению показателя 2(D¢ - d_s)/d_s в уравнении (2.5) и, как следствие к уменьшению коэффициента диффузии D. То обусловлено увеличением числа «мертвых» концов макромолекулы (ответвлений, поперечных связей и т.д.), куда может попасть молекула газа-диффузанта, не достигнув микрополости свободного объема для дальнейшей диффузии [66]. Для подтверждения этих положений на рис. 2.19 и 2.20 приведены зависимости коэффициентов диффузии D и растворимости s для ПЭВП от обратной величины  в двойных логарифмических координатах, соответствующие уравнениям (2.5) и (2.18).Как можно видеть, для коэффициента диффузии (третий сомножитель в правой части уравнения (2.37)) эта зависимость распадается на два участка: на первом (большие ) зависимость D от масштаба измерения гораздо сильнее, чем на втором (малые ). Для первого участка наклон прямой D равен ~ 9,1, а для второго - D = 3,7, что хорошо согласуется с величиной показателя 2(D¢-d_s)/d_s при D¢ = D_f = 5,4 и D¢ = d_f = 2,77, соответственно. Из данных рис. 2.20 следует, что аналогичная зависимость s(1/ ) аппроксимируется единственной прямой с наклоном D = 5,88, что вновь хорошо соответствует величине D_f [65].

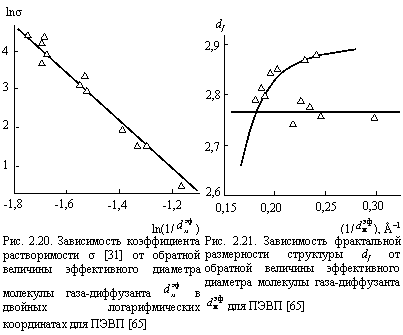
По существу аналогичный физический смысл имеет мультифрактальная трактовка процессов газопереноса. На рис. 2.21 приведена зависимость d_f от 1/ , т.е., от масштаба измерения, для ПЭВП, из которой следует, что эта зависимость, как и показанная на рис. 2.19, распадается на две ветви: монофрактальную с d_f = const и мультифрактальную, где d_f является функцией 1/ . Очевидно, если d_f и, согласно уравнению (1.41) D_f, не зависят от , то это означает структурный механизм диффузии при D¢ = d_f. Зависимость d_f или D_f от 1/  предполагает, что молекула газа-диффузанта «ищет» более высокоэнергетическое место на поверхности микрополости свободного объема) как следует из данных рис. 2.21, мультифрактальный участок зависимости d_f(1/ ) лежит выше монофрактального и поэтому соответствует более высоким значениям D_f). Это приводит к повышенным значениями как s, так и D, что в конечном итоге увеличивает a_ik [65].

Таким образом, обе рассмотренные выше фрактальные трактовки процессов газопереноса в непористых полимерных мембранах достаточно точно описывают коэффициент разделения углеводородов по метану для полиэтилена. Эти трактовки имеют общий физический смысл: зависимость размерности структуры, контролирующей процессы газопереноса, от масштаба измерения, т.е., эффективного диаметра молекулы газа-диффузанта.