Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

2.3. Фрактальная модель перколяции флуктуационного свободного объема и молекулярная подвижность

Как уже отмечалось, в настоящее время предполагается [4; 5; 28],что диффузия газов через полимерные мембраны реализуется прохождением молекул газа через микрополости свободного объема и в этом смысле свободный объем является аналогом пористости в кристаллических твердых телах (см. уравнение (2.5)). Однако, для прохождения молекул диффузанта через полимер необходимо образование сквозных каналов или, иначе говоря, перколяционного каркаса микрополостей. При этом в случае перекрывающихся сфер порог перколяции равен 0,34 ± 0,01 [17], что намного больше максимально возможной величины относительного свободного объема f_c = 0,159 для полимеров [67]. Авторы [68; 69] дали этому эффекту два альтернативных объяснения и вывели на их основе количественную модель газопереноса с привлечением представлений фрактального анализа и теории перколяции.

В рамках теории перколяции был выполнен расчет порога перколяции Х_с для протекания по перекрывающимся статистически расположенным сферам, который дал следующий результат [17]:

,                             (2.38)

где N_c - критическое число сфер диаметром d в объеме.

Очевидно, в рассматриваемом случае в качестве Х_с следует принять величину относительного флуктуационного свободного объема f_c, в качестве N_c - число его микрополостей на единицу объема N_h, а в качестве d - диаметр микрополости d_h. Величины f_c и объема микрополости V_h могут быть рассчитаны из уравнений (2.6) и (2.7), соответственно, а величина N_h - следующим образом [53]:

.                                                            (2.39)

Из уравнения (2.38) следует, что показатель 3 для диаметра сферы d предполагает ее моделирование как трехмерного объекта. Замена этого показателя на D_f позволяет моделирование микрополостей как D_f-мерных сфер, и согласно уравнению (2.38) в этом случае можно получить фрактальную величину порога перколяции . На рис. 2.22 приведена зависимость (Т) для ПЭВП в интервале Т = 173 ¸ 293 К. Как следует из этого графика, при Т = 253 ¸ 273 К величина  становится больше порога перколяции Х_с = 0,34 ± 0,01 и это означает, что в такой трактовке микрополости образуют сквозные каналы, облегчающие диффузию газов через полимер.

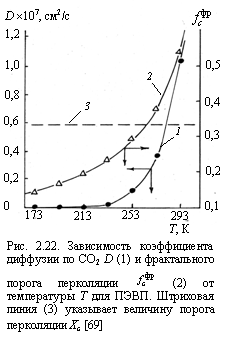
На рис. 2.22 также приведена рассчитанная по уравнению (2.21) зависимость D(T) для диффузии СО₂ в ПЭВП. Как следует из сравнения зависимостей (Т) и D(T), наблюдается их симбатность и резкий рост D происходит в том же интервале температур, где реализуется условие  » Х_с = 0,34. Таким образом, существуют два режиму диффузии, отвечающих условиям  < X_c и  > X_c. Первом режиме молекула газа «ожидает» образования микрополости флуктуационного свободного объема рядом с микрополостью, где она в данный момент находится, после чего реализуется ее перескок на величину несколько ангстрем, примерно равную d_h [9]. Этот режим можно назвать «последовательным». Во втором случае реализуется диффузия молекулы газа через сквозные перколяционные каналы, которые формируют микрополости, моделируемые D_f-мерной сферой, что существенно (на несколько порядков) увеличивает D. По аналогии с предыдущим этот режим был назван «параллельным» [68; 69].

Проблема диффузии газов в полимерах тесно связана с вопросом молекулярной подвижности [7]. Усиление молекулярной подвижности приводит к интенсификации диффузии. В рамках предлагаемой модели эта корреляция объясняется следующим образом [69]. Как показано в работе [71], количественно уровень молекулярной подвижности характеризуется фрактальной размерностью D_ц участка цепи между физическими зацеплениями или узлами химической сшивки (1 < D_ц £ 2). Величину D_ц можно оценить из уравнения [71]:

.                          (2.40)

На рис. 2.23 приведена зависимость D_ц(Т) для ПЭВП, из которой следует рост D_ц по мере увеличения Т. Особый интерес для настоящего изложений представляют предельные температуры, при которых достигаются предельные значения D_ц = 1 и D_ц = 2. В первом случае предельная температура Т₁, полученная экстраполяцией графика рис. 2.23 к D_ц = 1, равна ~ 138К, что соответствует температуре замораживания b-подвижности Т* в полимерах (для ПЭВП Т* = 140 ¸ 150 К [19]). В рамках фрактального анализа эта температура соответствует температуре реализации квазиравновесного состояния структуры, для которого D_ц = 1, т.е., цепь полностью вытянута между точками фиксации и ее подвижность заморожена (для ПЭВП Т₁ » 160 К [72]). Расчет по уравнению (2.21) показывает, что при Т = 140 К D = 4,13 ´ 10^-14 cм²/с, а при Т = 293 К D = 3,90 ´ 10^-8 cм²/с. Иначе говоря, замораживание молекулярной подвижности приводит к уменьшению D примерно на 6 порядков, т.е., практически до нуля.

При D_ц = 2 экстраполяция графика рис. 2.23 дает Т₂ » 485 К, что примерно равно температуре перехода «жидкость 1 - жидкость 2» T_ll, определяемой по уравнению (1.43). При этой температуре наблюдается переход к бесструктурной жидкости, т.е., истинному каучуку, для которого D_ц = 2 [56]. При Т = 485 К величина D, рассчитанная согласно данным [9], равна для диффузии СО₂ в ПЭВП ~ 3,57 ´ 10^-5 cм²/с, т.е., на 3 порядка больше величины D при Т = 273 К. Эти результаты позволяют получить простое эмпирическое соотношение между D и D_ц [69]:

,                                       (2.41)

которое демонстрирует очень сильную зависимость диффузии газов через полимеры от уровня молекулярной подвижности в последних. Очевидно, что приближенное уравнение (2.41) корректно только для диффузии СО₂ в ПЭВП.

Далее рассмотрим простую физическую интерпретацию D_f-мерной сферы. Стенки микрополости флуктуационного свободного объема представляют собой поверхность сегментов макромолекул, колеблющихся вокруг своих равновесных положений. Чем выше температура испытаний, тем больше фрактальные размерности D_f и D_ц, характеризующие степень энергетической возбужденности структуры и уровень молекулярной подвижности, соответственно, тем больших размеров могут достигать микрополости, пока при определенной температуре они не сформируют осциллирующий перколяционный каркас, что приводит к существенному росту коэффициента диффузии. Следовательно, рост D_f и D_ц означает фактическое увеличение размеров микрополости.

Обобщение уравнения (2.41) на примере диффузии углеводородов в ПВТМС получено в работе [73]. Было обнаружено, что для ПВТМС в интервале Т = 293 ¸ 403 К наблюдается систематическое увеличение D_ц в пределах 1,046 ¸ 1,590, сопровождаемое ростом D. Это позволило аналитически выразить соотношение между D и D_ц в форме степенной функции [73]:

,                                                           (2.42)

где К и D - константы для каждого газа-диффузанта.

Сравнение температурных зависимостей D для двух газов (С₂Н₄ и С₃Н₈), рассчитанных по уравнениям (2.21) и (2.42), приведено на рис. 2.24. Как можно видеть, получено хорошее соответствие зависимостей D(T), рассчитанных обоими методами.

Величины констант К и D в уравнении (2.42) обнаружили систематическое изменение с вариацией диаметра молекулы газа-диффузанта d_м, что следует из данных табл. 2.5. Это систематическое изменение позволило выразить указанные константы с помощью следующих уравнений [73]:

,                                                  (2.43)

.                                          (2.44)

Как следует из уравнений (2.43) и (2.44), наблюдается очень сильная степенная зависимость К и D (и, следовательно, коэффициента диффузии) от величины d_м. Аналогичная сильная зависимость D(d_м) подтверждается и экспериментально: так, при переходе от Не (d_м = 1,82 Å) к С₄Н₁₀ (d_м = 5,66 Å) величина D в случае ПВТМС уменьшается почти на 6 порядков [30; 31].

Таблица 2.5

Значения констант K и D в уравнении (2.42) для углеводородов [73]

Углеводород	dм, Å [30]	K	D
C2H4	4,17	1,060	1,37
C2H6	4,44	0,390	2,80
C3H6	4,99	0,137	4,18
C3H8	5,12	0,034	9,30

Для проверки общности соотношений (2.42) ¸ (2.44) был выполнен расчет D по ним для ПВТМС и 10 газов-диффузантов, чья величина d_м изменялась в указанном выше интервале (d_м = 1,82 ¸5,66 Å). Сравнение экспериментальных [30; 31] и рассчитанных указанным способов коэффициентов диффузии для ПВТМС приведено в табл. 2.6. Как можно видеть, несмотря на существенную погрешность для некоторых газов (например, Не), расчет дает корректный интервал изменения D при Т = 293 К, а именно, на 6 порядков величины. В общем случае такая погрешность обусловлена самой степенной формой соотношений (2.42) ¸ (2.44) и большими величинами показателей в них [73].

Таблица 2.6

Сравнение экспериментальных и рассчитанных по уравнению (2.42) коэффициентов диффузии для ПВТМС [73]

Газ	dм, Å [30; 31]	D, cм2/с
		Эксперимент [30; 31]	Расчет по уравнениям (2.42) ¸ (2.44)
He	1,82	370	1660
Ne	2,30	95	139
O2	2,89	7,6	7,2
CO2	3,02	5,0	4,1
N2	3,04	3,6	3,7
CH4	3,18	1,8	2,1
Rn	3,77	0,08	0,23
C2H2	3,38	0,64	0,93
C4H6	3,85	0,80	0,17
C4H10	5,66	0,001	0,003

Таким образом, изложенные выше результаты показали, что величина коэффициента диффузии разных газов в ПВТМС контролируется двумя факторами: степенью молекулярной подвижности, характеризуемой фрактальной размерностью D_ц, и размером молекул газа-диффузанта. Как и в случае ПЭВП (уравнение (2.41)), получена очень сильная степенная зависимость D от обоих указанных факторов, объясняющая очень большую вариацию D для ограниченного интервала изменения D_ц = 1,046 ¸ 1,590 и d_м = 1,82 ¸ 5,66 Å [73].