Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.1. Зависимость периода кристаллической решетки от температуры
Зависимость периода кристаллической решетки от температуры определяет физическую сущность коэффициента теплового расширения и температурные зависимости модуля упругости, коэффициента Пуассона, предела упругости, предела текучести, коэффициента теплового расширения, коэффициента теплопроводности, плотности.
Допущения расчетной модели
1. Рассматривается элементарная атомная ячейка кристаллической решетки монокристалла (кристаллита в поликристалле).
2. Кристаллическая решетка находится в равновесном состоянии (кулоновские силы притяжения уравновешены силами отталкивания).
3. Потенциальная энергия взаимодействия зарядов U0 – величина постоянная, то есть решается статическая задача.
4. Расчет изменения периода кристаллической решетки вследствие повышения температуры основан на учете изменения энергии связи двух разноименных зарядов в атомной ячейке кристаллической решетки, т.е. между узлом решетки и электронным облаком в межузловом пространстве.
Энергия электростатической связи двух разноименных зарядов атома в кристаллической решетке в соответствие с законом Кулона определяется по формуле
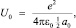
где e = 1,6⋅10–19 Кл – элементарный заряд, равный по модулю заряду электрона; p = 3,14; ε0 = 8,85⋅10–12 Кл2 /Н⋅м2 – электрическая постоянная; а0 – период кристаллической решетки; а0 /2 – расстояние между разноименными зарядами (узлом кристаллической решетки и электронной оболочкой).
Тепловая энергия атома при нагреве ячейки монокристалла на величину DТ определяется как
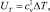
где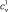 
– теплоемкость атома при постоянном объеме. В соответствии с законом Дюлонга и Пти
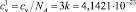Дж/К,
где NA – число Авогадро.
Энергия связи двух разноименных зарядов атома в ячейке кристаллической решетки вследствие нагрева уменьшается на величину
∆U = U0 – UT.
Изменение среднего расстояния между зарядами вследствие нагрева кристаллической решетки
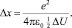
Изменение периода кристаллической решетки вследствие нагрева
∆а0 = ∆x – а0 /2.
После преобразований зависимость изменения периода кристаллической решетки от температуры примет следующий вид [1]
Результаты расчета а0 в зависимости от температуры для некоторых металлов приведены в табл. 1.1.
Графическая зависимость периода кристаллической решетки от температуры, в частности, для хрома приведена на рис. 1.1.
Из табл. 1.1 и рис. 1.1 видно, что результаты расчета а0 в зависимости от температуры удовлетворительно сходятся (с расхождением до 3,3 %) с экспериментальными данными работы [2]. На рис. 1.2 приведены экспериментальные зависимости [2].
Результаты расчета периода кристаллической решетки а0 в зависимости от температуры в дальнейшем используются для определения:
– коэффициента теплового расширения;
– модуля упругости;
– предела упругости и др. характеристик.
Выводы
1. Полученная формула позволяет определять теоретическую зависимость периода кристаллической решетки от температуры и сократить объем экспериментов.
2. Результаты расчета периода кристаллической решетки от температуры определяют физическую сущность коэффициента теплового расширения и температурные зависимости модуля упругости, коэффициента Пуассона, предела упругости, предела текучести, коэффициента теплового расширения, коэффициента теплопроводности, плотности.
Таблица 1.1
|
T, °С |
а0 |
а0эксп для W |
Расхождение, % |
а0 |
а0эксп для Mo |
Расхождение, % |
а0 |
а0эксп для Cr |
Расхождение, % |
а0 |
а0эксп для Nb |
Расхождение, % |
а0 |
а0эксп для V |
Расхождение, % |
|
20 |
3,165 |
3,165 |
0,00 |
3,147 |
3,147 |
0,00 |
2,884 |
2,884 |
0,00 |
3,3 |
3,3 |
0,00 |
3,027 |
3,027 |
0,00 |
|
100 |
3,174 |
3,166 |
0,25 |
3,156 |
3,149 |
0,22 |
2,891 |
2,885 |
0,21 |
3,31 |
3,303 |
0,21 |
3,035 |
3,032 |
0,10 |
|
200 |
3,183 |
3,167 |
0,51 |
3,165 |
3,151 |
0,44 |
2,899 |
2,887 |
0,42 |
3,32 |
3,305 |
0,45 |
3,044 |
3,034 |
0,33 |
|
300 |
3,192 |
3,17 |
0,69 |
3,174 |
3,153 |
0,67 |
2,907 |
2,891 |
0,55 |
3,33 |
3,307 |
0,70 |
3,052 |
3,036 |
0,53 |
|
400 |
3,202 |
3,171 |
0,98 |
3,183 |
3,155 |
0,89 |
2,914 |
2,894 |
0,69 |
3,34 |
3,310 |
0,91 |
3,06 |
3,039 |
0,69 |
|
500 |
3,211 |
3,172 |
1,23 |
3,192 |
3,157 |
1,11 |
2,922 |
2,897 |
0,86 |
3,35 |
3,313 |
1,12 |
3,069 |
3,042 |
0,89 |
|
600 |
3,22 |
3,174 |
1,45 |
3,201 |
3,16 |
1,30 |
2,93 |
2,9 |
1,03 |
3,36 |
3,315 |
1,36 |
3,077 |
3,045 |
1,05 |
|
700 |
3,229 |
3,175 |
1,70 |
3,21 |
3,162 |
1,52 |
2,937 |
2,904 |
1,14 |
3,37 |
3,318 |
1,57 |
3,086 |
3,048 |
1,25 |
|
800 |
3,239 |
3,177 |
1,95 |
3,22 |
3,165 |
1,74 |
2,945 |
2,907 |
1,31 |
3,38 |
3,323 |
1,72 |
3,094 |
3,053 |
1,34 |
|
900 |
3,248 |
3,178 |
2,20 |
3,229 |
3,167 |
1,96 |
2,953 |
2,91 |
1,48 |
3,391 |
3,325 |
1,98 |
3,103 |
3,057 |
1,50 |
|
1000 |
3,258 |
3,18 |
2,45 |
3,238 |
3,169 |
2,18 |
2,961 |
2,915 |
1,58 |
3,401 |
3,327 |
2,22 |
3,112 |
3,060 |
1,70 |
|
1100 |
3,267 |
3,181 |
2,70 |
3,248 |
3,171 |
2,43 |
2,969 |
2,92 |
1,68 |
3,411 |
3,330 |
2,43 |
3,12 |
3,065 |
1,79 |
|
1200 |
3,277 |
3,183 |
2,95 |
3,257 |
3,174 |
2,61 |
2,976 |
2,922 |
1,85 |
3,422 |
3,333 |
2,67 |
3,129 |
3,070 |
1,92 |
|
1300 |
3,287 |
3,185 |
3,20 |
3,267 |
3,176 |
2,87 |
2,984 |
2,927 |
1,95 |
3,432 |
3,336 |
2,88 |
3,138 |
3,075 |
2,05 |
|
1400 |
3,296 |
3,188 |
3,39 |
3,277 |
3,178 |
3,12 |
2,992 |
2,934 |
1,98 |
3,443 |
3,340 |
3,08 |
3,147 |
3,079 |
2,21 |
|
1500 |
3,306 |
3,19 |
3,64 |
3,286 |
3,182 |
3,27 |
3,001 |
2,94 |
2,07 |
3,454 |
3,343 |
3,32 |
3,156 |
3,084 |
2,33 |
|
1600 |
– |
3,192 |
– |
– |
3,185 |
– |
– |
2,948 |
– |
– |
3,347 |
– |
– |
– |
– |
|
2000 |
– |
3,2 |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
Примечание. Величина периода кристаллической решетки а0 приведена в ангстремах. Экспериментальные значения а0эксп взяты из работы [2].
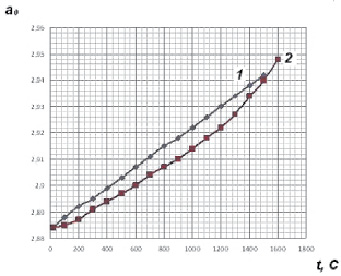
Рис. 1.1. Графическая зависимость периода кристаллической решетки (в ангстремах) от температуры для хрома:1 – эксперимент [2]; 2 – расчет
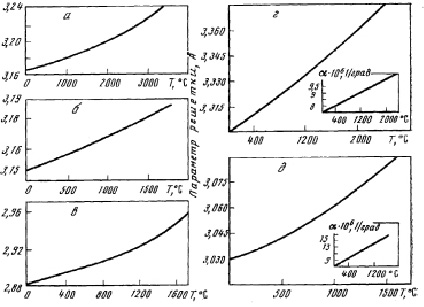
Рис. 1.2. Экспериментальные зависимости [2]: а – W; б – Mo; в – Cr; г – Nb; д – V