Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОТ ЧЕТЫРЕХ К ОДНОМУ. СИЛЫ ВНУТРИАТОМНОГО ВЗАИМОДЕЙСТВИЯ И ПРОЧНОСТЬ МАТЕРИАЛОВ

Бадамшин И. Х.,

1.2. Модуль упругости

Модуль упругости определяется на основе учета сил межатомного взаимодействия в соответствии со следующей моделью.

Допущения

1. Рассматривается элементарная атомная ячейка.

2. В атомной ячейке выделяется плотноупакованная плоскость.

3. В плоскости выбирается кристаллографическое направление.

4. В направлении рассматривается взаимодействие двух элементарных зарядов, на которое распространяется закон Кулона.

5. Решается статическая задача в условиях равновесия сил притяжения и отталкивания в кристаллической решетке.

Формула расчета модуля упругости выводится на основе моделей кристаллографии, закона Гука и закона Кулона.

Известно, что закон Кулона имеет следующий вид

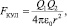
где Q1, Q2 – взаимодействующие заряды, Кл; e0 = 8,85⋅10–12 Кл2 /Н⋅м2 – электрическая постоянная; r – расстояние между взаимодействующими зарядами.

Закон Гука

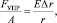
где А – площадь рассматриваемого сечения, м2; Dr / r – относительное удлинение рассматриваемого объема тела; Е – модуль упругости.

Известно также, что силы упругости в твердом теле обусловлены кулоновскими силами межатомного взаимодействия, поэтому

FУПР = FКУЛ,

где FУПР – сила упругости; FКУЛ – кулоновская сила взаимодействия зарядов. По определению модуля упругости Dr = r, отсюда следует, что

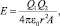
или для двух взаимодействующих элементарных зарядов [3–6]

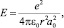
где r – расстояние между ближайшими соседями-атомами.

Схема расчета: в элементарной атомной ячейке рассматривается плотноупакованная плоскость; в свою очередь, в плоскости – кристаллографическое направление; затем, вдоль этого направления рассматривается два взаимодействующих заряда.

Например, для монокристалла железа Fe а0 = 2,8665∙10–10 м; расстояние между ближайшими соседями-атомами в объемно-центрированной решетке (ОЦК) 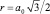. Расстояние между ближайшими разноименными зарядами в кристаллографическом направлении ⟨100⟩ 0,5а0.

Тогда

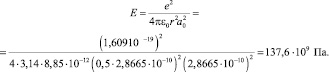
Расстояние между ближайшими разноименными зарядами в кристаллографическом направлении ⟨110⟩ 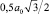. Тогда

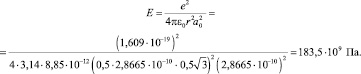
Результаты расчета модуля упругости Е для бездефектной кристаллической решетки меди и железа сведены в табл. 1.2.

Таблица 1.2

Результаты расчета и экспериментальные значения модуля упругости нитевидных монокристаллов (усов)

Из табл. 1.2 видно, в частности, что для меди в направлении ⟨111⟩ расчетный модуль упругости по базовой формуле равен 108,4 ГПа.

В соответствии со схемой расчета, переходя от взаимодействия двух зарядов к группе зарядов в плотноупакованной плоскости, необходимо учитывать ее ретикулярную плотность.

В данном случае коэффициент ретикулярной плотности для плоскости (111) равен

kr = (1/8)·3 + (1/2)·3 = 1,875.

Тогда с учетом ретикулярной плотности kr = 1,875 для плоскости 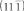модуль упругости в направлении ⟨111⟩ будет равен

Е = 108,4·1,875 = 203,2 ГПа.

Экспериментальное значение – 194 ГПа. Расхождение с результатом эксперимента в этом случае снижается с 44 % (табл. 1.2) до 4,7 %.