Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ОТ ЧЕТЫРЕХ К ОДНОМУ. СИЛЫ ВНУТРИАТОМНОГО ВЗАИМОДЕЙСТВИЯ И ПРОЧНОСТЬ МАТЕРИАЛОВ

Бадамшин И. Х.,

1.2.2. Зависимость модуля упругости от температуры

Приведенные в данном разделе таблицы (табл. 1.4–1.21) и графики (рис. 1.3–1.16) позволяют восполнить недостающие экспериментальные данные результатами расчетов. Здесь E100, E110 , E111 – расчетные значения модуля упругости монокристалла в соответствующих кристаллографических направлениях <100>, <110>, <111>. Экспериментальные значения из справочников обозначены индексами «ЭКСП». Расхождение в процентах – ∆E, %.

Медь Cu

Таблица 1.4

Температура, °C

Величина параметра в зависимости от температуры

E100,
ГПа

E100эксп,
ГПа

∆E, %

E110, ГПа

E110эксп,
ГПа

∆E, %

E111, ГПа

E111эксп,
ГПа

∆E, %

Eполи, ГПа

Eполи.эксп,
ГПа

∆E, %

20

90,8

66,7

36,1

136,2

131

3,9

185,2

194

4,5

128,6

129 [7]

0,31

100

89,1

–

–

133,7

–

–

181,8

–

–

127,4

–

–

200

86,9

–

–

130,3

–

–

177,2

–

–

125,7

–

–

300

84,1

–

–

126,2

–

–

171,6

–

–

123,5

–

–

400

80,9

–

–

121,3

–

–

165,0

–

–

120,9

111 [7]

8,9

500

77,2

–

–

115,8

–

–

157,5

–

–

117,8

–

–

600

73,2

–

–

109,8

–

–

149,3

–

–

114,3

95 [7]

20,3

700

68,8

–

–

103,2

–

–

140,4

–

–

110,4

–

–

800

64,2

–

–

96,3

–

–

130,9

–

–

106,1

–

–

900

59,4

–

–

89,1

–

–

121,1

–

–

101,4

–

–

1000

54,4

–

–

81,6

–

–

111,0

–

–

96,4

65 [7]

48,3

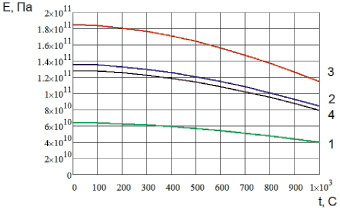
pic_1_3.tif

Рис. 1.3. Температурная зависимость модуля упругости монокристалла меди Cu: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>; 3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

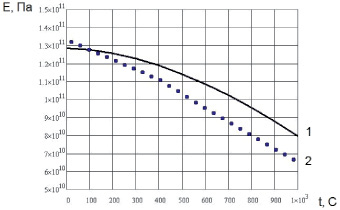
pic_1_4.tif

Рис. 1.4. Температурная зависимость модуля упругости поликристалла меди Cu: 1 – расчетные значения; 2 – экспериментальные значения [7]

Из табл. 1.4 и рис. 1.3, 1.4 видно, что значительный объем недостающих экспериментальных данных восполняется расчетными данными, имеющими удовлетворительную сходимость.

Необходимо отметить, что с увеличением температуры расхождение возрастает. Это связано с тем, что в элементах, имеющих невысокую температуру плавления (Cu, Al и др.), начинаются процессы разрушения кристаллической решетки под воздействием температуры, близкой к температуре плавления, что не учитывается данной моделью.

Алюминий Al

Таблица 1.5

Температура, °C

Величина параметра в зависимости от температуры

E100, ГПа

E100 эксп,
ГПа

∆E, %

E110,
ГПа

E110 эксп,
ГПа

∆E, %

E111,
ГПа

E111 эксп,
ГПа

∆E, %

Eполи, ГПа

Eполи эксп,
ГПа

∆E, %

20

47,7

62,5

23,7

71,5

71,4

0,1

97,3

75,1

29,6

72,2

70,8 [7]

2,0

100

47,1

–

–

70,6

–

–

96,0

–

–

71,3

–

–

200

46,2

–

–

69,4

–

–

94,3

–

–

70,0

63,8 [7]

9,7

300

45,2

–

–

67,8

–

–

92,1

–

–

68,4

–

–

400

43,9

–

–

65,8

–

–

89,5

–

–

66,4

54,9 [7]

20,9

500

42,3

–

–

63,5

–

–

86,4

–

–

64,1

–

–

600

40,6

–

–

60,9

–

–

82,8

–

–

61,4

49,2 [7]

24,8

700

38,7

–

–

58,0

–

–

78,9

–

–

58,5

–

–

800

36,6

–

–

54,9

–

–

74,6

–

–

55,3

–

–

900

34,3

–

–

51,4

–

–

70,0

–

–

51,9

–

–

1000

31,9

–

–

47,8

–

–

65,0

–

–

48,3

–

–

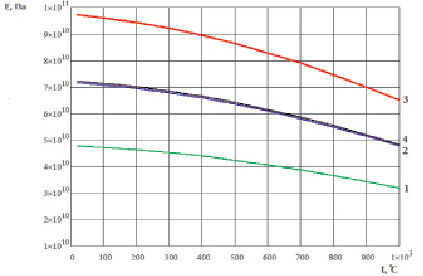
pic_1_5.tif

Рис. 1.5. Температурная зависимость модуля упругости монокристалла алюминия Al: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>; 3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

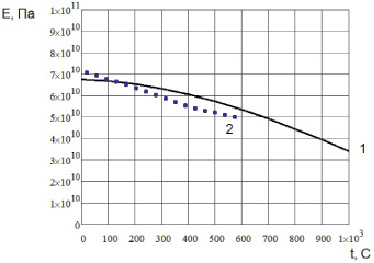
pic_1_6.tif

Рис. 1.6. Температурная зависимость модуля упругости поликристалла алюминия Al: 1 – расчетные значения; 2 – экспериментальные значения [7]

Никель Ni

Таблица 1.6

Температура, °C

Величина параметра в зависимости от температуры

E100,
ГПа

E100 эксп,
ГПа

∆E, %

E110, ГПа

E110 эксп,
ГПа

∆E, %

E111, ГПа

E111 эксп, ГПа

∆E, %

Eполи, ГПа

Eполи эксп,
ГПа

∆E, %

20

140,6

138,0

1,8

210,9

215,0

1,9

286,7

262,0

9,4

212,7

196[7]

8,5

100

138,0

–

–

207,0

–

–

281,5

–

–

208,8

–

–

200

134,6

–

–

201,9

–

–

274,6

–

–

203,7

–

–

300

130,5

–

–

195,7

–

–

266,1

–

–

197,4

–

–

360

–

–

–

–

–

–

–

–

–

194

187[7]

3,7

400

125,6

–

–

188,3

–

–

256,1

–

–

190,0

–

–

500

120,0

–

–

180,0

–

–

244,8

–

–

181,6

–

–

600

113,9

–

–

170,9

–

–

232,3

–

–

172,4

–

–

700

107,3

–

–

160,9

–

–

218,8

–

–

162,3

–

–

800

100,3

–

–

150,4

–

–

204,5

–

–

151,7

–

–

900

92,9

–

–

139,4

–

–

189,5

–

–

140,6

–

–

1000

85,386

–

–

128,1

–

–

174,1

–

–

129,2

–

–

1100

77,7

–

–

116,6

–

–

158,5

–

–

117,6

–

–

1200

70,0

–

–

105,1

–

–

142,8

–

–

106,0

–

–

1300

62,4

–

–

93,7

–

–

127,4

–

–

94,5

–

–

1400

55,0

–

–

82,5

–

–

112,2

–

–

83,3

–

–

1500

47,9

–

–

71,8

–

–

97,7

–

–

72,5

–

–

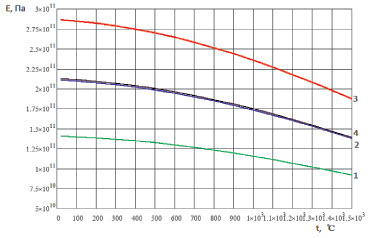
pic_1_7.tif

Рис. 1.7. Температурная зависимость модуля упругости монокристалла никеля Ni: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>; 3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

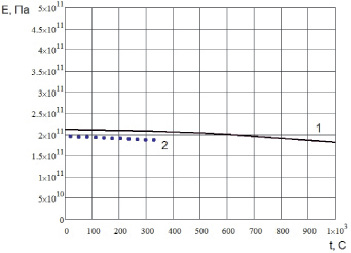
pic_1_8.tif

Рис. 1.8. Температурная зависимость модуля упругости поликристалла никеля Ni: 1 – расчетные значения; 2 – экспериментальные значения [7]

Ниобий Nb

Таблица 1.7

Температура, °C

Величина параметра в зависимости от температуры

E100, ГПа

E100 эксп, ГПа

∆E, %

E110, ГПа

E110 эксп, ГПа

∆E, %

E111, ГПа

E111 эксп, ГПа

∆E, %

Eполи, ГПа

Eполи эксп,
ГПа

∆E, %

20

51,9

–

–

134,7

–

–

155,1

–

–

113,9

119[7]

4,3

100

51,5

–

–

133,9

–

–

154,2

–

–

113,2

–

–

200

51,0

–

–

132,6

–

–

152,7

–

–

121,1

–

–

300

51,4

–

–

131

–

–

150,8

–

–

110,7

–

–

400

49,6

–

–

129

–

–

148,5

–

–

109

108[7]

0,9

500

48,7

–

–

126,6

–

–

145,7

–

–

107

–

–

600

47,7

–

–

123,8

–

–

142,5

–

–

104,7

–

–

700

46,5

–

–

120,7

–

–

139

–

–

102

–

–

800

45,1

–

–

117,2

–

–

135

–

–

99,1

–

–

900

43,7

–

–

113,4

–

–

130,6

–

–

95,9

–

–

1000

42,1

–

–

109,3

–

–

125,9

–

–

92,5

–

–

1100

40,4

–

–

105

–

–

120,9

–

–

88,7

–

–

1200

38,6

–

–

100,3

–

–

115,5

–

–

84,8

73,5[7]

15,4

1300

36,7

–

–

95,4

–

–

109,9

–

–

80,7

–

–

1400

34,8

–

–

90,3

–

–

104

–

–

76,4

–

–

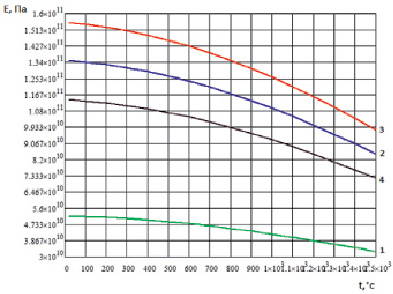
pic_1_9.tif

Рис. 1.9. Температурная зависимость модуля упругости монокристалла ниобия Nb: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>; 3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

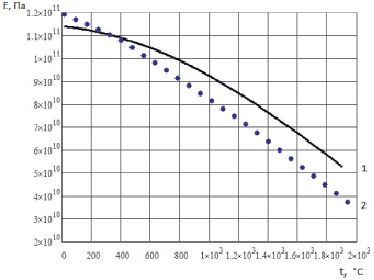
pic_1_10.tif

Рис. 1.10. Температурная зависимость модуля упругости поликристалла ниобия Nb: 1 – расчетные значения; 2 – экспериментальные значения [7]

Вольфрам W

Таблица 1.8

Температура, °C

Величина параметра в зависимости от температуры

E100, ГПа

E100 эксп, ГПа

∆E, %

E110, ГПа

E110 эксп,
ГПа

∆E, %

E111, ГПа

E111 эксп,
ГПа

∆E, %

Eполи, ГПа

Eполи эксп,
ГПа

∆E, %

20

323,8

389

16,8

420,6

389

8,1

484,3

389

24,5

409,6

393,8[7]

4

100

323,1

–

–

419,6

–

–

483,2

–

–

408,6

–

–

200

322

–

–

418,2

–

–

481,5

–

–

407,2

–

–

300

320,5

–

–

416,3

–

–

479,4

–

–

405,4

–

–

400

318,7

–

–

414

–

–

476,7

–

–

403,2

–

–

500

316,6

–

–

411,3

–

–

473,5

–

–

400,5

–

–

600

314,1

–

–

408,1

–

–

469,8

–

–

397,3

–

–

700

311,3

–

–

404,4

–

–

465,6

–

–

393,8

–

–

800

308,2

–

–

400,4

–

–

461

–

–

389,8

371 [7]

5,1

900

304,8

–

–

395,5

–

–

455,8

–

–

385,5

–

–

1000

301

–

–

391

–

–

450,2

–

–

380,7

–

–

1100

296,6

–

–

385,7

–

–

444

–

–

375,5

–

–

1200

292,5

–

–

380

–

–

437,5

–

–

370

–

–

1300

287,8

–

–

373,9

–

–

430,5

–

–

364

–

–

1400

282,8

–

–

367,4

–

–

423

–

–

357,7

–

–

1500

277,6

–

–

360,5

–

–

415,1

–

–

351,1

–

–

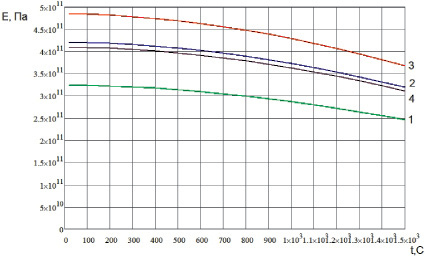
pic_1_11.tif

Рис. 1.11. Температурная зависимость модуля упругости монокристалла вольфрама W: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>; 3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

График температурной зависимости модуля упругости поликристалла вольфрама W приведен на рис. 1.12.

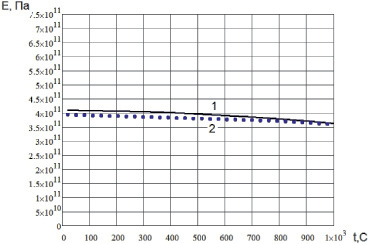
pic_1_12.tif

Рис. 1.12. Теоретическая зависимость модуля упругости поликристаллического W от температуры: …… – экспериментальные значения [7]

График температурной зависимости модуля упругости поликристалла хрома Cr приведен на рис. 1.13.

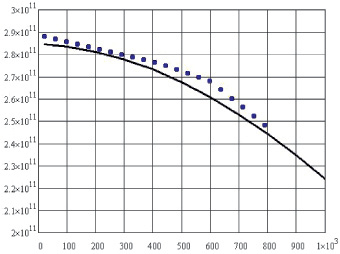
pic_1_13.tif

Рис. 1.13. Теоретическая зависимость модуля упругости поликристаллического Cr от температуры: …… – экспериментальные значения [7]

Двойные соединения

Карбид ниобия NbC

Таблица 1.9

Температура, °C

Величина параметра в зависимости от температуры

E100, ГПа

E100 эксп, ГПа

∆E, %

E110, ГПа

E110 эксп, ГПа

∆E, %

E111, ГПа

E111 эксп, ГПа

∆E, %

Eполи, ГПа

Eполи эксп, ГПа

∆E, %

20

621,5

–

–

466,2

–

–

485,9

–

–

524,5

540[11]

3

100

619,3

–

–

464,8

–

–

484,5

–

–

522,9

–

–

200

616,4

–

–

462,9

–

–

482,6

–

–

520,6

–

–

300

612,7

–

–

460,5

–

–

480

–

–

517,7

–

–

400

608,3

–

–

457,5

–

–

476,9

–

–

514,2

–

–

500

603,2

–

–

454

–

–

473,2

–

–

510,1

–

–

600

597,3

–

–

449,9

–

–

469

–

–

505,4

–

–

700

590,8

–

–

445,3

–

–

464,2

–

–

500,1

–

–

730

  

–

–

  

–

–

  

–

–

  

500[11]

–

800

583,6

–

–

440,2

–

–

458,8

–

–

494,2

–

–

900

575,7

–

–

434,5

–

–

453

–

–

487,7

–

–

1000

567,1

–

–

428,4

–

–

446,6

–

–

480,7

–

–

1100

557,9

–

–

421,8

–

–

439,7

–

–

473,1

–

–

1200

548,1

–

–

414,7

–

–

432,3

–

–

465

–

–

1230

  

–

–

  

–

–

  

–

–

  

470[11]

–

1300

537,7

–

–

407,1

–

–

424,4

–

–

456,4

–

–

1400

526,7

–

–

399,1

–

–

416

–

–

447,3

–

–

1500

515,1

–

–

390,6

–

–

407,2

–

–

437,6

–

–

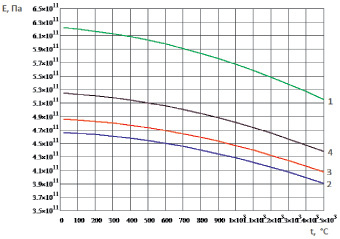
pic_1_14.tif

Рис. 1.14. Температурная зависимость модуля упругости монокристалла карбида ниобия NbC: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>;
3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

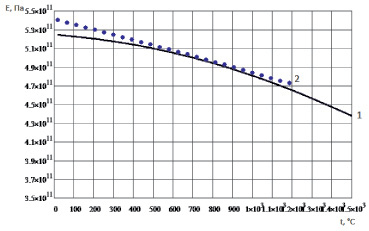
pic_1_15.tif

Рис. 1.15. Температурная зависимость модуля упругости поликристалла карбида ниобия NbC: 1 – расчетные значения; 2 – экспериментальные значения [11, 12]

Силицид ниобия Nb5Si3

Таблица 1.10

Температура, °C

Величина параметра в зависимости от температуры

E100, ГПа

E100 эксп,
ГПа

∆E, %

E110, ГПа

E110 эксп,
ГПа

∆E, %

E111, ГПа

E111 эксп, ГПа

∆E, %

Eполи, ГПа

Eполи эксп, ГПа

∆E, %

20

406,7

–

–

154,5

–

–

169,0

–

–

–

–

–

100

405,6

–

–

154,1

–

–

168,5

–

–

–

–

–

200

404,6

–

–

153,6

–

–

167,9

–

–

–

–

–

300

403,6

–

–

153,1

–

–

167,4

–

–

–

–

–

400

402,5

–

–

152,7

–

–

166,8

–

–

–

–

–

500

401,4

–

–

152,2

–

–

166,3

–

–

–

–

–

600

400,3

–

–

151,7

–

–

165,7

–

–

–

–

–

700

399,2

–

–

151,1

–

–

165,1

–

–

–

–

–

800

398,1

–

–

150,6

–

–

164,4

–

–

–

–

–

900

396,9

–

–

150,0

–

–

163,8

–

–

–

–

–

1000

395,7

–

–

149,4

–

–

163,1

–

–

–

–

–

1100

394,5

–

–

148,8

–

–

162,3

–

–

–

–

–

1200

393,2

–

–

148,1

–

–

161,5

–

–

–

–

–

1300

319,8

–

–

147,3

–

–

160,7

–

–

–

–

–

1400

390,4

–

–

146,5

–

–

159,7

–

–

–

–

–

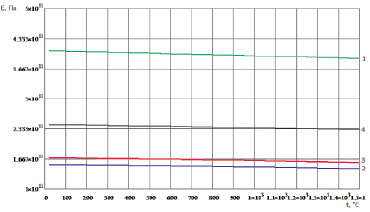
pic_1_16.tif

Рис. 1.16. Температурная зависимость модуля упругости монокристалла пентаниобия трисилицида Nb5Si3: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>; 3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

Алюминид никеля Ni3Al

Таблица 1.11

Температура, °C

Величина параметра в зависимости от температуры

E100, ГПа

E100 эксп,
ГПа

∆E, %

E110, ГПа

E110 эксп, ГПа

∆E, %

E111, ГПа

E111 эксп,
ГПа

∆E, %

Eполи, ГПа

Eполи эксп,
ГПа

∆E, %

0

114,2

–

–

171,3

–

–

232,9

230

1,3

172,8

178

3,3

100

113,3

–

–

170,0

–

–

234,1

–

–

171,5

–

–

200

112,1

–

–

168,1

–

–

228,6

–

–

169,6

–

–

300

110,5

–

–

165,7

–

–

225,3

–

–

167,2

–

–

400

108,6

–

–

162,8

–

–

221,4

–

–

164,3

–

–

500

106,3

–

–

159,4

–

–

216,7

–

–

160,8

–

–

600

103,7

–

–

155,5

–

–

211,4

–

–

156,9

–

–

700

100,7

–

–

151,1

–

–

205,5

–

–

152,4

–

–

800

97,5

–

–

146,3

–

–

198,9

215

7,5

147,6

–

–

900

94,0

–

–

141,0

–

–

191,7

210

8,7

142,2

–

–

1000

90,2

–

–

135,3

–

–

184,0

155

18,7

136,5

–

–

1100

86,2

–

–

129,3

–

–

175,8

120

46,5

130,4

–

–

1200

81,9

–

–

122,9

–

–

167,1

80

108,9

124,0

–

–

1300

77,5

–

–

116,2

–

–

158,0

–

–

117,2

–

–

1400

72,8

–

–

109,2

–

–

148,5

–

–

110,2

–

–

1500

68,0

–

–

102,0

–

–

138,7

–

–

102,9

–

–

Из табл. 1.11 видно, что величина расхождения при температурах 1100 и 1200 °С возрастает с 46,5 до 108,9 %. Это объясняется тем, что данная модель не учитывает растворение интерметаллидной фазы, которое начинается с температуры примерно 900 °С (рис. 1.17). Например, для монокристалла интерметаллида Ni3Al известны экспериментальные данные [13] в кристаллографическом направлении <111>. Результаты расчета имеют удовлетворительную сходимость до температуры 900 °С (рис. 1.17). Экспериментальные значения – из работы [13].

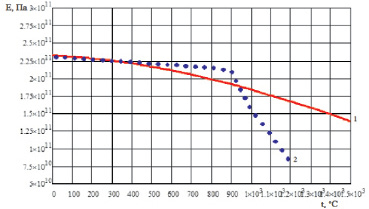
pic_1_17.tif

Рис. 1.17. Температурная зависимость модуля упругости интерметаллида Ni3Al в направлении <111>: 1 – расчетные значения; 2 – экспериментальные значения [13]

С учетом этих данных рассчитаны зависимости для направлений <100>, <110> и для поликристаллического состояния (рис. 1.18), что существенно дополняет недостающую экспериментальную информацию.

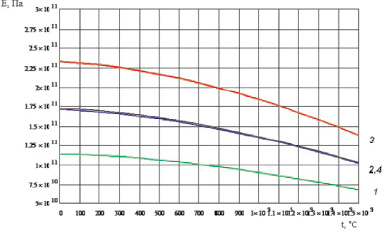
pic_1_18.tif

Рис. 1.18. Температурная зависимость модуля упругости монокристалла интерметаллида Ni3Al: 1 – модуль упругости в направлении <100>; 2 – модуль упругости в направлении <110>; 3 – модуль упругости в направлении <111>; 4 – модуль упругости поликристалла

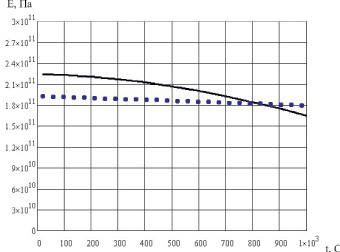
pic_1_19.tif

Рис. 1.19. Температурная зависимость модуля упругости поликристалла NiAl:_____ – расчет; …… – эксперимент

Модуль упругости монокристаллических жаропрочных никелевых сплавов определяется матрицей монокристалла, т.е. g – твердым раствором, основой которого является кристаллическая решетка никеля (табл. 1.12).

Таблица 1.12

Наименование сплава или элемента и направление действия нагрузки

Величина модуля упругости, ГПа

Расхождение, %

расчетная

экспериментальная

Ni (ГЦК) <100>

<110>

<111>

140,2

210,3

262,9

138,0

215,0 [7]

262,0

1,6

2,1

0,3

ЖС 6Ф моно <100>

<110>

<111>

140,2

210,3

262,9

139[14]

220

305

0,9

4,5

13,8

ЖС 32 <100>

<110>

<111>

140,2

210,3

262,9

135…140 [15]

–

280…300

3,8…0

–

6,0…12,3

ЖС 36 моно <100>

<110>

<111>

140,2

210,3

262,9

130[14]

215

305

7,8

2,3

13,8

Экспериментальные значения для ЖС 36 моно и ЖС 6Ф моно взяты из графика в [14].

Установлено, что расчетные значения модуля упругости монокристаллических жаропрочных никелевых сплавов в кристаллографическом направлении <100> имеют удовлетворительную сходимость с экспериментом с расхождением от 0,9 до 7,8 % (табл. 1.12). Полученные результаты позволяют обоснованно использовать модельную композицию Ni – NbC для оценки прочности лопатки из материала типа ВКЛС с кристаллографическим направлением <100> в области упругих деформаций.

Необходимо отметить также, что для кристаллографических направлений <110>, <111> максимальное расхождение расчета для рассматриваемых материалов (табл. 1.12) составляет 13,8 % (в частности, для сплава ЖС 36 моно).

На рис. 1.21, 1.22 приведены расчетные температурные зависимости модуля упругости для сплавов ЖС6Ф <001> и ЖС36моно <111> [16] в сравнении с экспериментальными данными [14].

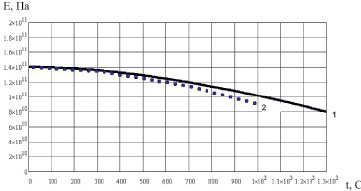
pic_1_20.tif

Рис. 1.20. Температурная зависимость модуля упругости сплава ЖС6Ф в направлении <001>: 1 – расчет; 2 – эксперимент [14]

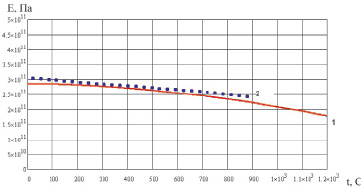
pic_1_21.tif

Рис. 1.21. Температурная зависимость модуля упругости сплава ЖС36моно в направлении <111>: 1 – расчет; 2 – эксперимент [14]

Приведенные данные показывают, что:

1. Значительный объем недостающих экспериментальных данных восполняется расчетными данными, имеющими удовлетворительную сходимость.

2. Результаты расчетов модуля упругости применимы для оценки упругих характеристик поликристаллов, в том числе и для соединений, модули упругости которых редко или совсем не встречаются в справочной литературе.

3. Результаты расчетов модуля упругости применимы для проектирования композитных материалов, используемых в газотурбинных двигателях.

4. Дальнейшими исследованиями необходимо дополнить расчетную модель учетом процессов растворения фаз при высоких температурах (рис. 1.18).