
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.2.3. Результаты моделирования упругих свойств наноструктур на основе углерода и кремния
Результаты расчета модуля упругости монокристаллов углерода, кремния и германия со структурой типа алмаз приведены в табл. 1.13 [17].
Таблица 1.13
|
Наименование элемента и направление действия нагрузки |
Величина модуля упругости, ГПа |
Расхождение, % |
|
|
расчетная |
экспериментальная [7] |
||
|
С (алмаз) ⟨100⟩ ⟨110⟩ ⟨111⟩ поликристалл |
912,2 1596 1460 1323 |
1052 1162 1202 1141 |
–13,3 37,3 21,5 16 |
|
Si ⟨100⟩ ⟨110⟩ ⟨111⟩ поликристалл |
130,2 227,8 208,4 188,8 |
131 175 199 162,7 |
–0,6 30,1 4,7 16 |
|
Ge ⟨100⟩ ⟨110⟩ ⟨111⟩ поликристалл |
81,0 141,8 129,8 117,5 |
102 137 155 132,3 |
–20,5 3,5 –16,3 –11,2 |
В частности, график изменения модуля упругости в зависимости от температуры для поликристалла германия приведен на рис. 1.22.
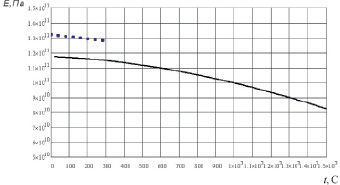
Рис. 1.22. Температурная зависимость модуля упругости поликристалла германия:
…… – эксперимент [7]; ______ – расчет
Из табл. 1.13 и рис. 1.22 видно, что результаты расчета модуля упругости для C, Si, Ge имеют удовлетворительную сходимость с результатами экспериментов других авторов [7]. Это позволяет прогнозировать свойства наноструктур на основе C и Si.
Так, для графена (или углеродной нанотрубки УНТ) со структурой, приведенной на рис. 1.23 [18], определены упругие характеристики.
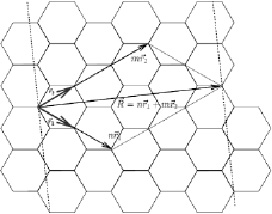
Рис. 1.23. Развертка углеродной нанотрубки [18]
В частности, теоретический график изменения модуля упругости в зависимости от температуры для УНТ или графена в направлении вектора r1 (или r2) приведен на рис. 1.24 [4].
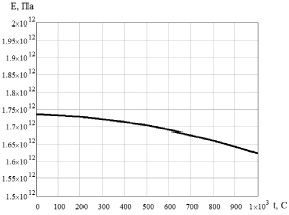
Рис. 1.24. Расчетная температурная зависимость модуля упругости графена (УНТ)
Аналогично для силицена, имеющего структуру, показанную на рис. 1.25 [19], также определены упругие характеристики.
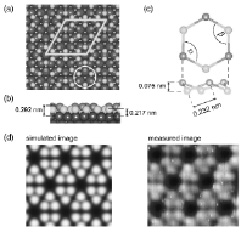
Рис. 1.25. Структура силицена [19]
Так, теоретический график изменения модуля упругости в зависимости от температуры для силицена в направлении вектора r1 (или r2) приведен на рис. 1.26.
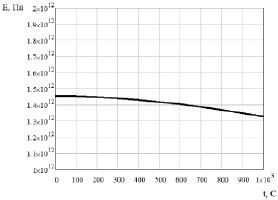
Рис. 1.26. Расчетная температурная зависимость модуля упругости силицена
Выводы
1. Разработанный метод позволяет использовать его для компьютерного моделирования материалов в условиях отсутствия экспериментальных данных.
2. Разработанный метод позволяет рассчитывать упругие, прочностные, физические и теплофизические характеристики бездефектных монокристаллов.
3. Зная соответствующие характеристики нанообъема монокристаллов, можно прогнозировать свойства композитов. В частности, можно оценить упругие, прочностные, физические и теплофизические характеристики композиции, состоящей из атомных слоев графена и силицена и др.
