Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.6.1. Коэффициент теплового расширения
В настоящее время задача учета межатомного взаимодействия в кристаллической решетке для определения коэффициента теплового расширения кристаллов решается различными способами.
Так, коэффициент теплового расширения a связан с температурой плавления и может характеризовать силу межатомной связи [2]. Максимальная сила межатомной связи приходится на металлы с максимальными температурами плавления и минимальными значениями коэффициента термического расширения. Соответственно эти металлы имеют и минимальные межатомные расстояния.
Для металлов с кубической решеткой коэффициент a связан с температурой плавления соотношением aТпл @ 0,02. Кроме того, для веществ с металлическим характером связи имеется эмпирическое соотношение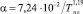 
[2]. Однако эти соотношения не позволяют установить зависимость коэффициента теплового расширения от эксплуатационной температуры.
Расчет a, учитывающий ангармоническую составляющую колебаний атомов, по формуле [36]
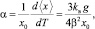
где g и b – функции потенциала U; x – расстояние; Т – температура, предполагает знание потенциала кристаллической решетки U и также не имеет методики инженерного расчета коэффициента теплового расширения.
Для оценки коэффициента теплового расширения по формуле Гилмана [2] необходимо знать силу межатомного сцепления sс
sс = 3k/(8αV),
где k – постоянная Больцмана; V – средний атомный объем.
Поэтому актуальной является задача инженерного расчета коэффициента теплового расширения применительно к моно- и поликристаллам материалов, в частности, лопаток газовых турбин.
Вследствие периодичности и симметрии бездефектного монокристалла свойства элементарной атомной ячейки передаются кристаллической решетке. Поэтому для атомной ячейки и кристаллической решетки в целом коэффициент теплового расширения определяется как
a = ∆а0 /(а0DТ).
Так, температурная зависимость коэффициента теплового расширения для хрома, меди, алюминида никеля приведены на рис. 1.34–1.36 [37].
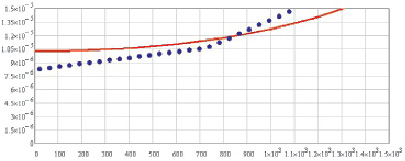
Рис. 1.34. Температурная зависимость коэффициента теплового расширения хрома Cr
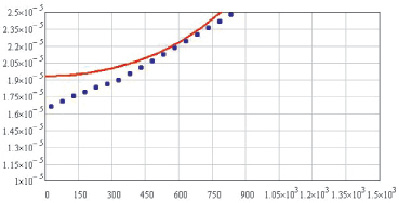
Рис. 1.35. Температурная зависимость коэффициента теплового расширения меди Cu
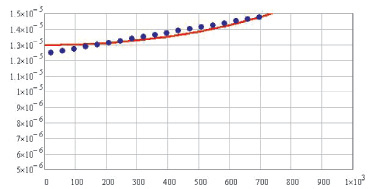
Рис. 1.36. Температурная зависимость
коэффициента теплового расширения алюминида никеля NiAl
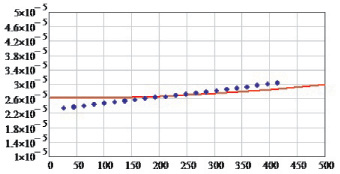
Рис. 1.37. Температурная зависимость коэффициента теплового расширения алюминия Al
Из рис. 1.34–1.37 видно, что результаты расчета удовлетворительно сходятся со справочными данными [7].
Выводы
1. Полученная формула позволяет определять теоретическую зависимость коэффициента теплового расширения от температуры и сократить объем экспериментов.
2. Результаты расчета коэффициента теплового расширения армирующей фазы и матрицы эвтектического композита или монокристалла являются исходными данными для оценки термических напряжений в материале лопатки турбины.