Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОТ ЧЕТЫРЕХ К ОДНОМУ. СИЛЫ ВНУТРИАТОМНОГО ВЗАИМОДЕЙСТВИЯ И ПРОЧНОСТЬ МАТЕРИАЛОВ

Бадамшин И. Х.,

1.6.2. Модель распространения колебаний и коэффициент теплопроводности

Явление распространения колебаний в твердых телах, в частности в кристаллах, имеет большое практическое значение в технике. С ним связаны процессы распространения колебаний в кристаллах и теплопроводность.

В данном разделе рассматривается модель скорости распространения колебаний в монокристаллах.

Допущения

1. Рассматривается неподвижная кристаллическая решетка, принятая в кристаллографии.

2. Не учитывается факт, что атомы являются осцилляторами.

3. Решается статическая задача из условия равновесия кулоновских сил притяжения и отталкивания между двумя ближайшими зарядами в элементарной атомной ячейке монокристалла.

4. Вследствие симметрии и периодичности бездефектного монокристалла свойства ячейки передаются макрообъему.

Скорость распространения колебаний в монокристаллах определяется по формуле, выведенной автором из условия равенства кинетической энергии колебания атома Uкин относительно узла кристаллической решетки

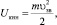(1.4)

вызванной внешним воздействием (например, тепловым), с одной стороны, и энергии электростатического противодействия атома Uэл внешнему воздействию, с другой стороны,

Uэл = е2 /4πε0r, (1.5)

где m = mA⋅1,66⋅10–27, кг – масса атома; mA – атомная масса химического элемента; u – скорость передачи колебаний от одного атома к другому (скорость звука); е –элементарный заряд, равный заряду электрона; r – расстояние между ближайшими атомами – соседями; ε0 – электрическая постоянная.

Тогда можно записать

mυ2 /2 = e2 /4πε0r.

Откуда скорость распространения колебаний u в моно- и поликристаллах [38]

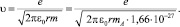(1.6)

Следует отметить, что соотношение (1.5) характеризует скорость распространения колебаний между двумя соседними зарядами в элементарной атомной ячейке кристаллической решетки.

В частности, для никеля с гранецентрированной кристаллической решеткой 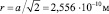. После подстановки е = 1,602⋅10–19 Кл и m = 58,7 (атомной массы никеля) получим значение скорости звука в моно- или поликристалле никеля Ni, равное 4380 м/с.

Результаты некоторых расчетов сведены в табл. 1.18.

Из табл. 1.18 видно, что расчетная величина скорости распространения колебаний для никеля Ni составляет 4380 м/с, а справочное значение [39] для υ3 – 4785 м/с. В табл. 1.18 приведены минимальные расхождения с расчетом. Поэтому по результатам сравнительного анализа из табл. 1.18 можно заключить, посредством каких волн распространяются колебания в данном химическом элементе. В частности, для алюминия это продольные волны, т.к. минимальное расхождение, соответствующее υ1, составляет 9,2 %. А для никеля – продольные и поперечные волны с расхождением 8,5 %.

Таблица 1.18

Результаты расчета скорости распространения колебаний

Расчет скорости распространения колебаний в монокристаллах необходим, в частности, для определения коэффициента теплопроводности.

Формула расчета коэффициента теплопроводности выводится в следующей последовательности [40].

Известно, что перенос энергии в форме теплоты подчиняется закону Фурье

j = –l(∆T /∆x),

где j – плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты Q в единицу времени t через единичную площадку A, перпендикулярную оси x, l – коэффициент теплопроводности; ∆T /∆x – градиент температуры, равный скорости изменения температуры на единицу длины x в направлении нормали к этой площадке.

Исходя из определения, закон Фурье можно записать в следующем виде

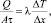
откуда

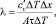
где 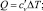 – теплоемкость одного атома, или

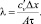
Допущения

1. Рассматривается элементарная ячейка монокристалла в виде куба со стороной, равной периоду кристаллической решетки а.

2. В качестве единичной площадки принимается .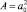

3. Единица времени t в элементарном объеме не равна одной секунде t ≠ 1 с, тогда время процесса передачи колебаний между двумя атомами в ячейке можно определить по формуле t = ∆x/u, где ∆x – расстояние между ближайшими соседями-атомами.

4. Колебания в ячейке атома распространяются в наиболее плотноупакованных плоскостях (рис. 1.38). В пределах одной кристаллографической плоскости могут распространяться одна или две плоские волны: продольная и (или) поперечная.

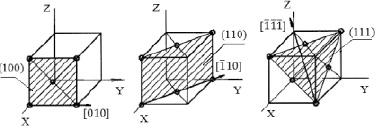
Рис. 1.38. Кристаллографические направления и плоскости ГЦК решетки

5. Теплоемкость одного атома постоянная величина и определяется в соответствии с законом Дюлонга и Пти, т.е.

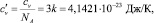
где NA – число Авогадро; k – постоянная Больцмана.

В общем случае теплоемкость одного атома зависит от температуры.

6. Коэффициент теплопроводности характеризует передачу тепла. Тепло в кристалле передается за счет кинетической энергии колебаний атомов в кристаллической решетке равной (mυ2)/2. Иначе говоря, в формуле расчета коэффициента теплопроводности необходимо учитывать массу. Масса учитывается через атомную массу элемента mА и коэффициент ретикулярной плотности kР элементарной атомной ячейки.

С учетом перечисленных допущений формула расчета коэффициента теплопроводности для монокристаллов примет следующий вид [40]

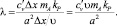(1.7)

Результаты расчетов для некоторых металлов сведены в табл. 1.19. Примечание: итоговое значение l оценивается, в частности, как сумма l для плотноупакованных плоскостей ячейки, либо как половина среднего значения l в соответствии с четвертым допущением. Справочные значения в табл. 1.19 приведены из работы [7].

Из табл. 1.19, в частности, видно, что расчетная величина коэффициента теплопроводности для меди Cu составляет 406 Вт/м⋅К, а справочное значение – 401,2 Вт/м⋅К [7], расхождение – 1,2 %.

Таким образом, удовлетворительная сходимость расчета с экспериментальными данными, полученными другими авторами, подтверждают адекватность разработанной модели.

Таблица 1.19

Результаты расчета коэффициента теплопроводности

Результаты оценки коэффициента теплопроводности являются исходными данными для расчета напряженно-деформированного состояния рабочей лопатки турбины, изготовленной из монокристаллических сплавов и эвтектических композитов.