
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.8. Термические напряжения
Допущения
1. Для расчета термических напряжений sтерм используется известная зависимость, справедливая для области упругих деформаций
sтерм = Еюнг⋅εt,
где Еюнг – модуль упругости; εt = α⋅∆t –термическая деформация; a – коэффициент теплового расширения; ∆t – перепад температуры.
2. Рассматривается термонапряженное состояние тонких кромок лопаток газовых турбин: входная и выходная кромки пера лопатки; тонкие стенки охлаждающих поверхностей внутренней полости пера лопатки.
3. Результаты сравнительных расчетов термических напряжений в пространственной и линейной постановках задачи дают практически совпадающие сведения о термонапряженности для области кромок лопаток [50].
Поскольку эквивалентное напряжение есть одноосное напряжение, эквивалентное сложно напряженному состоянию, то одноосные термические напряжения сравниваются с эквивалентными.
4. В линейной постановке задачи более нагретые части сжимаются, а менее нагретые – растягиваются [51].
В более нагретых частях стержня возникают сжимающие температурные напряжения. Физически это объясняется тем, что крайние волокна стержня получают большую температурную деформацию и при отсутствии поперечных связей стержня деформируются так, как показано на рис. 1.42, а. Поперечные связи удерживают крайние волокна (рис. 1.42, б), создавая в них напряжения сжатия, а в менее нагретых частях стержня – растяжение.
Рис. 1.42. Картина температурных деформация в стержне: а – поперечные связи отсутствуют, б – в конце стержня имеется жесткая пластина
Комментарии к рис. 1.42. Рассматривается одноосное растяжение двух неодинаково нагретых участков. Поперечные сечения остаются плоскими и перпендикулярными к оси (гипотеза плоских сечений), температура при нагреве каждого участка равномерно распределена по объему. В результате нагрева (или охлаждения) каждый из участков будет иметь неодинаковую деформацию вследствие различных температур (рис. 1.43).
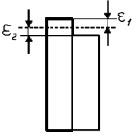
Рис. 1.43. Схема термического расширения
неодинаково нагретых двух участков тела
Как видно из рис. 1.43, результатом такого взаимодействия является средняя деформация, обозначенная пунктиром.
5. Для определения термической деформации в направлении распространения теплового потока (температуры) в линейной постановке задачи модель, приведенная в работе [51], преобразована в следующий вид (рис. 1.44).
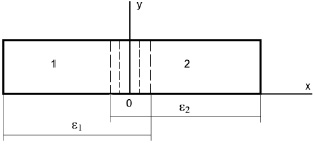
Рис. 1.44. Схема одноосного деформирования
при неодинаковом нагреве участков 1 и 2
Тогда средняя величина деформации в соответствии со схемой одноосного деформирования при неодинаковом нагреве участков 1 и 2 тела определяется по формуле
∆e = ε1 /2 + (– ε2 /2),
где ε1/2 – средняя деформация первого участка; ε2 /2 – средняя деформация второго участка.
Пример решения задачи при одноосном деформировании.
В основе моделирования лежат экспериментальные исследования, проведенные в институте проблем прочности АН УССР (рис. 1.45) [50, 52].
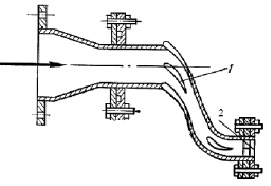
Рис. 1.45. Однолопаточная камера для моделирования условий теплосмен
с целью определения реальных тепловых состояний:
1 – сопловая лопатка; 2 – искусственное регулирование гидравлическое сопротивление [52]
В частности, определяются термические напряжения в сопловой лопатке газовой турбины из материала ХН75ВМЮ (ЭИ827), где перепад температур на входной или выходной кромках (на участках толщиной 3 мм) лопатки составляет tмах = 630 °C и tмin = 460 °C в течение 15 с термоцикла (рис. 1.46).
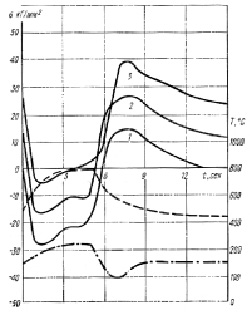
Рис. 1.46. Изменение напряжений (сплошные линии), температуры (штриховая линия)
и перепад температур (штрихпунктирная линия) на входной кромке модели лопатки
на режиме 450–800 °С при наложении статической растягивающей нагрузки:
1 – σ = 0; 2 – σ = 12 кГ/мм2; 3 – σ = 24 кГ/мм2 [52]
Результаты расчета
Рассматривается цикл нагрева – охлаждения длительностью 15 с [52]. Результаты расчета одноосного нагружения приведены на рис. 1.47.
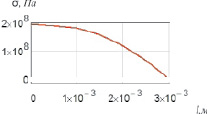
Рис. 1.47. Изменение термических напряжений по толщине кромки лопатки
Проведен сравнительный расчет сложнонапряженного состояния 3D-модели лопатки методом конечных элементов.
Выявлено, что при одноосном и сложнонапряженном нагружениях термические напряжения на выходной кромке лопатки одного порядка составляют 196–208 МПа (рис. 1.47). Аналогичное схождение результатов получено и для входной кромки лопатки до уровня 140 МПа.
Таким образом, получена удовлетворительная сходимость результатов расчета термических напряжений по двум методикам с результатами эксперимента других авторов [52].
