Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.9. Ползучесть
В расчетах на прочность рабочих лопаток газовых турбин важной составляющей является деформация ползучести. В этом случае деформация, определяющая напряженно-деформированное состояние лопатки, выражается как суммарная деформация eS
eS = eупр + et + e0,
где eупр – относительная упругая деформация; et – относительная термическая деформация; e0 – относительная деформация ползучести.
Для применения известной [8] формулы скорости деформации ползучести x по модели Нортона x = ksn необходимо знать экспериментальные значения коэффициентов k, n, информация по которым ограничена [8, 53]. Возникает задача определения характеристик ползучести в условиях ограниченных экспериментальных данных.
Задача решается созданием математической модели расчета характеристик ползучести, основанной на перемещении краевых дислокаций. Такая модель позволяет получить диаграмму установившейся ползучести для конкретного материала в зависимости от температуры и напряжения.
Рассматривается деформация на I участке и на II участке установившейся ползучести (рис 1.48). В этом случае для определения величины деформации ползучести необходимо знать скорость перемещения дислокации.
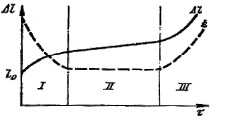
Рис. 1.48. Типичный вид кривой ползучести Dl(t) и скорости ползучести x(t):
I – стадия неустановившейся ползучести; II – стадия установившейся ползучести;
III – стадия разрушения
Вначале рассматривается движение одной краевой дислокации в бездефектном монокристалле. Начальная скорость перемещения дислокации в нанообъеме u0 определяется по формуле [54, 55]
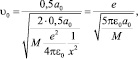(1.8)
где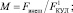 
Fвнеш – внешняя сила; 
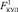– кулоновская сила взаимодействия двух зарядов.
Зная скорость перемещения дислокации в нанообъеме, рассчитывается деформация в монокристалле.
Скорость деформации ползучести технических монокристаллов, имеющих плотность дислокаций до 103 см–2, определяется по формуле Орована
x = rd bu, (1.9)
где x – скорость деформации ползучести; rd – плотность дислокаций; b – вектор Бюргерса (параметр, характеризующий геометрическое искажение кристаллической решетки вследствие появления краевой дислокации); u – скорость движения дислокации (в частом случае u = u0).
Эта же формула (1.9) используется для расчета скорости деформации ползучести поликристаллов. В этом случае расчет ведется при следующих допущениях.
1. Рассматривается установившаяся ползучесть (I и II участки).
2. Механизм ползучести определяется перемещением краевых дислокаций.
3. Изменение плотности дислокаций (в том числе, межзеренное и внутризеренное для поликристаллов) учитывается формулой Орована (1.9).
4. Влияние температуры на скорость деформации учитывается через изменение периода кристаллической решетки а0 и плотность дислокаций.
5. Влияние напряжения на скорость деформации учитывается через изменение коэффициента.
Определение скорости перемещения краевой дислокации u по длине нанообъема под действием заданной внешней нагрузки дает возможность оценить величину и скорость деформации установившейся ползучести. Расчетная модель корректируется по ограниченным экспериментальным данным и в дальнейшем используется для определения характеристик ползучести при различных температурах и напряжениях внутри заданного интервала.
Последовательность расчета деформации ползучести следующая.
1. Рассчитывается начальная скорость перемещения дислокации по формуле (1.8).
2. По экспериментальным значениям скорости деформации x (при данных температуре и напряжении) определяется средняя плотность дислокаций rd по формуле (1.9)
rd = x/(а0u).
3. Расчетные значения плотности дислокаций подставляются в формулу Орована, тем самым определяется зависимость скорости деформации x от напряжения и температуры x = f(s,t).
4. Влияние температуры на скорость деформации x определяется также через изменение периода кристаллической решетки а0 по формуле (см. п. 1.1)
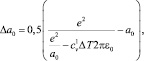
где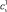 
– теплоемкость атома при постоянном объеме; DТ – изменение температуры. Затем величина Dа0 подставляется в формулу Орована.
5. Деформация e на I участке и II участке установившейся ползучести определяется, в частности, по формуле [93]
e = xtmexpxt,
где t – длительность испытаний на ползучесть; m = 0,3.
6. Ограничением величины деформации ползучести является нормативная величина, равная 0,2 %.
Примеры реализации методики расчета
Пример 1
Некоторые результаты расчета приведены на рис. 1.49, 1.50 (нулевая линия является технической).
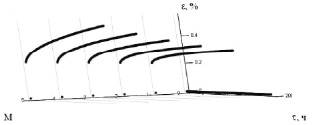
Рис. 1.49. Модельная диаграмма ползучести сплава при температуре t1
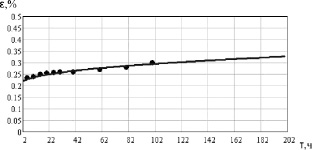
Рис. 1.50. Модельная диаграмма ползучести сплава при температуре t1
По справочным экспериментальным данным корректируется модель диаграммы ползучести. Затем по скорректированной модели прогнозируются неизвестные характеристики ползучести. В частности, при другом уровне температуры такие зависимости приведены на рис. 1.51, 1.52.
Модель позволяет достраивать диаграммы ползучести жаропрочного сплава на основе ограниченного объема экспериментальных данных.
Исходные расчетные данные формируются в условиях сокращения объема экспериментов, что снижает экономические и временные затраты в процессе проектирования лопаток газовых турбин.
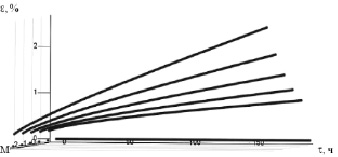
Рис. 1.51. Модельная диаграмма ползучести сплава при температуре t2
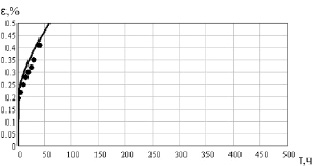
Рис. 1.52. Соответствие модельной диаграммы ползучести сплава при температуре t2
при s = const справочным данным
Адекватность модели подтверждается удовлетворительной сходимостью со справочными данными.
Пример 2
Результаты моделирования ползучести сплава ЖС26 представлены на рис. 1.53–1.56.
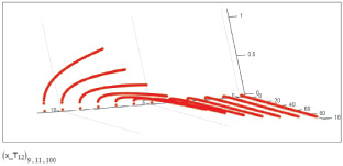
Рис. 1.53. Расчетная диаграмма ползучести ЖС26 в зависимости от напряжения при 900 °С
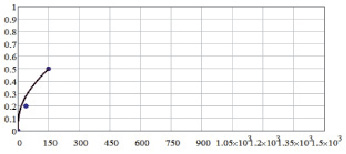
Рис. 1.54. Результаты расчета диаграмм ползучести сплава ЖС26
при температуре 900 °С, s = 309 МПа:___– расчетные; ....… – справочные значения [53]
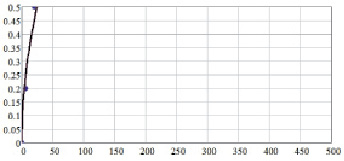
Рис. 1.55. Результаты расчета диаграмм ползучести сплава ЖС26 при температуре 900 °С, s = 400 МПа:___– расчетные; • – справочные значения [53]
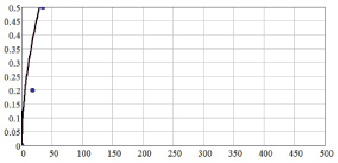
Рис. 1.56. Результаты расчета диаграмм ползучести сплава ЖС26 при температуре 1000° С, s = 300 МПа:___– расчетные; • – справочные значения [53]
Адекватность модели подтверждается удовлетворительной сходимостью с экспериментальными данными из работы [53].
Пример массива деформаций ползучести при температуре 900 °С приведен на рис. 1.57.
В результате получен массив деформаций ползучести, который в дальнейшем используется для построения диаграмм релаксации (п. 1.10) данного сплава, а также в модели малоцикловой усталости (п. 1.11).