Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.12.1. Моделирование кристаллической структуры
Для новых материалов характерна весьма ограниченная информация об упругих и прочностных характеристиках, необходимая в расчетах напряженно-деформированного состояния лопаток. В этих условиях возникает потребность в теоретических методах расчета упругих, прочностных характеристик, основанных на учете сил межатомного взаимодействия, так как классические методы расчета механики деформируемого твердого тела, основанные на гипотезе сплошности среды, не позволяют этого сделать.
При отсутствии экспериментальных данных разработанный метод позволяет моделировать элементарную атомную ячейку, ее характеристики и свойства бездефектных монокристаллов, в частности, в составе эвтектического композита для лопаток газовых турбин. Исходными данными являются химическая формула соединения, пространственная группа и символ Пирсона.
Рассматривается моделирование кристаллической структуры и ее упругих характеристик бездефектных монокристаллов в составе эвтектического композита
Nb–Nb5Si3 для лопаток газовых турбин в условиях ограниченного объема экспериментальных данных.
Исходными данными для расчета модуля упругости являются кристаллическая структура элементарной атомной ячейки монокристалла и ее период (рис. 1.63).
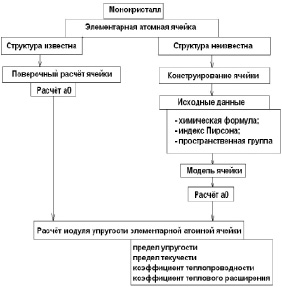
Рис. 1.63. Блок-схема последовательности расчета
Известными данными является химическая формула соединения Nb5Si3 и его параметры кристаллической структуры. В соответствии с символом Пирсона tI32 и пространственной группой I4/mcm [61] моделируется элементарная ячейка кристаллической структуры Nb5Si3 при следующих допущениях.
1. Элементарная ячейка выбирается в кристаллической структуре на основе следующих правил [43]: форма элементарной атомной ячейки должна по своей симметрии соответствовать симметрии кристалла; выбираемая ячейка должна иметь максимально возможное число прямых углов; объем элементарной атомной ячейки должен быть минимальным.
В результате получена 8-атомная модель элементарной ячейки Nb5Si3 по схеме замещения (рис. 1.64), кратная ячейке с 32 атомами.
Данная модель ячейки соответствует определенным пунктам описания структуры, приведенной в работе [62]. В частности, атомы кремния (как и ниобия) образуют вертикальные цепи, параллельные оси c. Расстояние Me–Si равно сумме атомных радиусов (0,3663 нм).
На рис. 1.65 представлена модель фрагмента элементарной ячейки Nb5Si3, которая является основой для дальнейших расчетов.
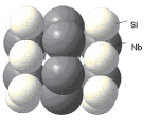
Рис. 1.65. Модель фрагмента элементарной ячейки Nb5Si3
Период модельной кристаллической решетки определяется в соответствии с известными правилами кристаллографии, а именно: зная металлические радиусы атомов и тип кристаллической решетки, определяется а0 из соотношения для расстояния между ближайшими соседями-атомами. Например, для ОЦК решетки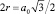 
, а для ГЦК – 
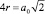[43].
Для расчета температурной зависимости модуля упругости компонентов композита используются следующие формулы:
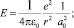
Адекватность методики апробирована на соединениях с известными структурными и упругими характеристиками. В частности, в табл. 1.24 приведены расчетные значения периода кристаллической решетки.
Из табл. 1.24 видно, что в результате расчета периода кристаллической решетки получена удовлетворительная сходимость со справочными данными для двойных соединений [43]. На основании этого, в результате расчета для модельной ячейки Nb5Si3 получено значение а0 = 3,663⋅10–10 м (рис. 1.64).
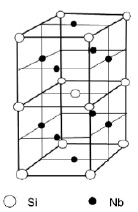
Рис. 1.64. Восьмиатомная модель элементарной атомной ячейки Nb5Si3 по схеме замещения
В качестве примера адекватности модели в табл. 1.25 приведены результаты расчета модуля упругости для монокристаллов-компонентов композита с известными характеристиками при температуре 20 °С.
Таблица 1.24
|
Наименование |
Величина периода кристаллической решетки, нм |
Расхождение, % |
|
|
расчетная |
справочная |
||
|
NbC |
0,444 |
0,4470 [43] |
–0,6 |
|
TaC |
0,446 |
0,4441 [43] |
0,4 |
|
Mo2C |
0,432 |
0,4254 [43] |
1,6 |
|
TiN |
0,432 |
0,4239 [43] |
1,9 |
|
Nb5Si3 (модель) |
0,3663 |
– |
– |
Таблица 1.25
|
Наименование элемента |
Величина модуля упругости, ГПа |
Расхождение, % |
|
|
расчетная |
справочная |
||
|
NbC (ОЦК) ⟨100⟩ ⟨110⟩ ⟨111⟩ поликристалл |
621,5 466,2 515,8 534,5 |
– – – 497; 504; 518; 550; 540 [63] |
– – – – |
|
TaC(ОЦК) ⟨100⟩ ⟨110⟩ ⟨111⟩ поликристалл |
637,8 478,3 529,3 548,5 |
– – – 515; 550; 730; 500 [63] |
– – – |
Упругие свойства матрицы композита Nb–Nb5Si3 определяются ее основой – кристаллической решеткой ниобия Nb типа ОЦК с периодом а0 = 3,3002⋅10–10 м. Поэтому исходные данные для расчета матрицы известны.
На основе модели кристаллической структуры силицида ниобия проведены расчеты упругих характеристик (табл. 1.26).
Получена теоретическая температурная зависимость модуля упругости бездефектного монокристалла Nb5Si3 с учетом анизотропии (рис. 1.16).
Таблица 1.26
|
Наименование элемента |
Величина модуля упругости, ГПа |
Расхождение, % |
|
|
расчетная |
справочная |
||
|
Nb (ОЦК) ⟨100⟩ ⟨110⟩ ⟨111⟩ поликристалл |
77,2 134,7 155,1 121,6 |
– – – 119 [7] |
– – – 2,3 |
|
Nb5Si3 ⟨100⟩ ⟨110⟩ ⟨111⟩ Si-Si ⟨110⟩ в (001) |
145,5 308,7 419,7 183,5 |
– – – – |
– – – – |
Выводы
1. Заложена основа метода моделирования кристаллической структуры и упругих свойств монокристалла.
2. Разработанный метод позволяет использовать его для компьютерного моделирования материалов в условиях отсутствия экспериментальных данных. В частности, смоделирована кристаллическая структура элементарной атомной ячейки Nb5Si3 по схеме замещения атомов и рассчитан ее период.
3. На основе модели кристаллической структуры ячейки получена теоретическая температурная зависимость модуля упругости Nb5Si3 с учетом анизотропии.