
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1.1. Физическая сущность механической модели
Существующая модель расчета ускорения силы тяжести g основана на законе всемирного тяготения и втором законе Ньютона. В соответствии с названными законами ускорение силы тяжести на поверхности Земли определяется по известному соотношению [70]
g = F/m = GM/R2,
где G – гравитационная постоянная; М = 5,98⋅1024 кг – масса Земли [71]; m – масса тела, находящегося на поверхности Земли; R – средний радиус Земли.
Расчетная модель основана на следующих предпосылках.
1. Рассмотрим тело, имеющее форму шара, движущееся в пространстве.
Первый случай
Если тело двигается только поступательно и прямолинейно без вращения под действием некоторого импульса, то точки А и В (рис. 2.1) имеют одинаковую линейную скорость V1 = V2. Центростремительное ускорение в этом случае отсутствует.
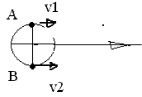
Рис. 2.1
Например, пушечное ядро, вылетевшее из ствола пушки, может совершать такое движение на прямолинейном участке траектории полета и т.п.
Второй случай
К телу привязывается нить, другой конец которой жестко закрепляется в точке О (рис. 2.2).
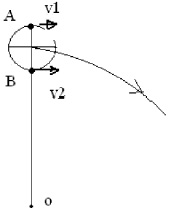
Рис. 2.2
Как и в первом случае, телу придается импульс. В отличие от первого случая тело будет совершать круговое движение с радиусом, равным длине нити. Кинетическая энергия, которой обладает движущееся тело, является источником центробежной силы, направленной от центра вращения наружу. Центробежная сила уравновешена силой сопротивления (упругости) нити. Поскольку тело движется по криволинейной траектории, то имеет место и центростремительное ускорение, которое вызвано силой сопротивления нити, именно она заставляет тело двигаться по окружности. Действительно, если нить перерезать (сила сопротивления нити равна нулю), равновесие нарушится и тело вылетит за пределы орбиты вращения.
При этом точки А и В (рис. 2.2) также имеют примерно одинаковую линейную скорость V1 ≈ V2 в случае, когда радиус орбиты значительно превышает радиус тела (рис. 2.2).
Третий случай
Если к поступательному прямолинейному движению (см. первый случай) рассматриваемого тела добавить вращение вокруг собственной оси (рис. 2.3), то необходимо сложить векторы орбитальной и вращательной скоростей.
Вследствие сложения векторов линейная скорость V1 в точке А будет больше, чем V2 в точке В (рис. 2.3)
V1 = Vорб + Vвр;
V2 = Vорб – Vвр.
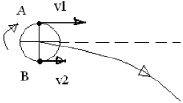
Рис. 2.3
Соответственно, импульс в точке А будет больше, чем в точке В при одинаковой массе m:
m⋅V1 > m⋅V2.
Иначе говоря, нижняя полусфера тела затормаживается по сравнению с верхней полусферой. Появляется крутящий момент в точке А относительно точки В (рис. 2.4).
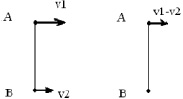
Рис. 2.4
Крутящий момент смещает центр масс в точке С рассматриваемого тела с прямолинейной траектории (пунктирная линия на рис. 2.3) в новое положение в точку С1
(рис. 2.5). В результате многократного смещения центра масс формируется криволинейная траектория (сплошная линия со стрелкой на рис. 2.3).
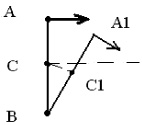
Рис. 2.5
Например, если ударить по бильярдному шару не точно по его центру, а с некоторым смещением от центра, то шар будет двигаться не только поступательно, но и одновременно вращаться. Это так называемый «крученый удар» заставляет шар двигаться по криволинейной траектории.
Иначе говоря, в данном случае роль силы упругости нити (которой здесь нет) играет центростремительная сила. Тело движется равномерно по криволинейной траектории, находясь в равновесии. Центробежная сила, вызванная кинетической энергией движения по орбите, уравновешена центростремительной силой, вызванной взаимодействием поступательного и вращательного движения тела.
Таким образом, совместное поступательное и вращательное движение тела является причиной возникновения центростремительного ускорения, вызывающего, в свою очередь, переход от прямолинейного к криволинейному движению.
