
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2.8. Теплоемкость материалов
В работах В.С. Ивановой, Г.Н. Третьяченко и Б.С. Карпиноса показано, что при числе циклов Nk, по достижении которого при напряжении, равном пределу выносливости, начинают возникать субмикроскопические трещины:
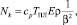
где β – коэффициент, учитывающий напряжения; cp – удельная теплоемкость;
TПЛ – температура плавления.
«Формула свидетельствует о том, что долговечность материала зависит от теплофизических свойств cp и TПЛ. Результаты экспериментов хорошо это подтверждают» [88].
В связи с этим возникает потребность расчетного определения теплоемкости материала.
Расчетная модель теплоемкости материалов основана на следующих допущениях.
Допущения
1. В основе расчета удельной теплоемкости материалов лежит вихревая модель атома. То есть материальной основой (физической сущностью) атома является «темная материя», обладающая свойствами жидкости (газа). Поэтому применимы законы механики жидкостей и газов.
2. Для расчета используется уравнение Майера и уравнение состояния для идеального газа Клапейрона – Менделеева.
Тогда теплоемкость при постоянном давлении cp определяется как
cp = cv + R = cv + pdVm /dT,
где cv – теплоемкость при постоянном объеме; R – молярная газовая постоянная;
p – давление; dVm – изменение молярного объема; dT – изменение температуры.
В соответствии с законом Дюлонга и Пти для моноатомных твердых тел cv = 3R [24]. Учитывая, что постоянная Больцмана
k = R/NA,
где NA – число Авогадро, можно записать R = k⋅NA.
Тогда теплоемкость при постоянном давлении одного атома
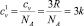
или
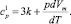
Таким образом, последнее выражение позволяет определять зависимость теплоемкости (при постоянном давлении) от температуры.
