Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СУБАТОМНЫЕ СОСТОЯНИЯ ВОДОРОДА

Неволин В. К.,

9. Спин и пространственная локализация свободных квантовых частиц

Неотъемлемым свойством квантовых частиц, как следует из предыдущих разделов, является наличие «собственной» энергии движения квантовых частиц совершающих инфинитное движение. Интересно рассмотреть собственное движение квантовых частиц не совершающих поступательное движение и вернуться к толкованию спина частиц.

К проблеме толкования спина для квантовых частиц подходят с различных точек зрения. Так в работе [1] автор приходит к заключению, что спин не связан с внутренней структурой квантовых частиц, а связан с волновыми полями, окружающими эти частицы и, в частности, электрона. В этой работе приведен обзор предыдущих подходов к теории спина, в том числе дираковская теория. Точку зрения, развиваемую в работе [1], можно обосновать с помощью нерелятивистких квантовых уравнений движения, что представляет методический интерес и является основой для решения известных квантовых задач (см. заключение).

На заре создания квантовой механики великий французский физик Луи де Бройль написал не только выражение для волны, носящей его имя и описывающей движение квантовых частиц, но один из первых предложил в своей докторской диссертации научному сообществу формулу [2]:

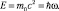(9.1)

Смысл этой формулы заключается в том, что элементарная частица с массой покоя m0 представляет собой «сгусток» энергии, который должен двигаться по законам квантовой механики. В силу формулы (9.1) для квантовых частицы должно существовать поле стоячих волн плотности вероятности. Луи де Бройлю удалось найти волновую электромагнитную аналогию этого явления для электрона [2, с. 203]. Известно шредингеровское «дрожание» дираковских электронов, связанное с колебаниями центра тяжести частицы и для проявления которого нужно привлечь волны с отрицательной энергией [2, с. 530].

Покажем, что решение квантовых уравнений движения в представлении плотности вероятности с энергией из формулы (9.1) позволяет, прежде всего, получить дискретный спектр значений спина у квантовых частиц с ненулевой массой покоя, а также представления о пространственном распределении плотности вероятности для свободных квантовых частиц.

Уравнения для инфинитного движения квантовой частицы массы m0 в произвольном внешнем поле 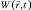в представлении плотности вероятности имеют вид [3–7]:

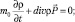(9.2)

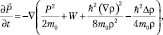(9.3)

где 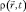 – пространственно-временное распределение плотности вероятности частицы;  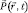– ее макроскопический импульс; W(r, t) – произвольная потенциальная энергия.

Для стационарного пространственно ограниченного свободного движения квантовой частицы система уравнений (9.2) и (9.3) запишется в виде:

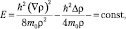(9.4)

где E = m0c2; ρ = ρ(r) – плотность вероятности распределения частицы в пространстве. Введем линейный масштаб задачи 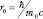. Это комптоновская длина волны. Для электрона r0 = 3,5∙10–11 см и она проявляется, например, при рассеянии пучка фотонов на свободных электронах. Тогда из (9.4) получим:

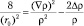(9.5)

Расположим сферическую систему координат в центре вероятностного распределения частицы, получим:

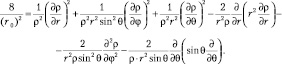(9.6)

Будем решать это уравнение методом разделения переменных:

ρ(r, θ, φ) = ρr(r)ρθ(θ)ρφ(φ).

Тогда

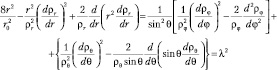(9.7)

Из (9.7) получим систему уравнений:

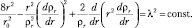(9.8)

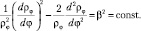(9.9)

И последнее уравнение:

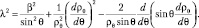(9.10)

Обратимся к уравнению (9.9), которое решается подстановкой 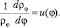Тогда 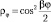и чтобы ρφ была однозначной функцией для константы β должны выполняться соотношения
β = 0, ±1, ±2, ±3, ... Введем квантовое число

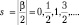
соответствующее спинам элементарных частиц, при этом ρφ = cos2s и 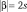. Спин является степенью свободы квантовых частиц и, как будет показано ниже, определяет пространственную структуру распределения плотности вероятности. На рис. 9.1 представлены распределения плотности вероятности ρφ(φ) при различных значения
спина частиц.

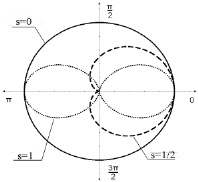
Рис. 9.1. Распределение плотности вероятности при движении по углу φ

Обратимся к решению уравнения (9.10). Будем искать решение этого уравнения в виде:

ρθ = sin θ2s.

Получим следующие соотношения для констант разделения переменных:

β2 = 4s2; λ2 = 4s + 4s2.

На рис. 9.2 показаны зависимости плотности вероятности ρθ(θ) при различных значениях спинового числа.

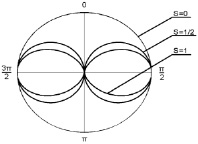
Рис. 9.2 Распределение плотности вероятности ρθ(θ) при различных значениях спинового числа

Из рисунка можно видеть, что чем больше спин частицы, тем меньше область распределения плотности вероятности по углу θ.

Обратимся к решению уравнения (9.8). Сделаем замену переменных:

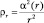и r = x∙r0.

Получим уравнение

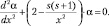(9.11)

Приближенное решение уравнения (9.11) для радиальной составляющей плотности вероятности запишем в виде суперпозиции асимптотик x → 0 и x → ∞, которые обеспечивают равенство второй производной 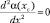в точке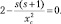

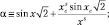
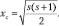(9.12)

Для частиц с нулевым спином это решение является точным и в размерных величинах записывается в виде осциллирующей и затухающей функций

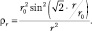(9.13)

На рис. 9.3 показано распределение радиальной плотности вероятности частиц с нулевым спином. Оно напоминает известный пакет для плоских волн де Бройля, который, как известно, расплывается со временем.

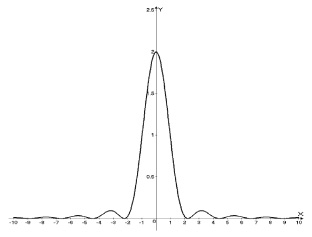
Рис. 9.3. Распределение радиальной плотности вероятности для частиц с нулевым спином.

Характерный радиус области локализации частицы равен

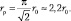(9.14)

Для частиц с ненулевым спином решение уравнения (9.11) является расходящимся при x → 0 и не интегрируем по объему частицы. Тогда следует предположить, что частицы с отличным от нуля спином имеют более сложную пространственную структуру движения, например, имеется полость с нулевой плотностью вероятности. На периферии частицы, как и прежде, имеется пространственно структурированное и осциллирующее распределение плотности вероятности в соответствии с формулой (9.13).

Характерный внешний радиус локализации частиц с отличным от нуля спином можно оценить в соответствии с (9.12) по формуле:

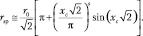(9.15)

Как видно из предыдущего, свободные частицы с отличным от нуля спином совершают вращательно-колебательные движения. Покажем, что в уравнении (9.11) должно выполняться соотношение:

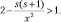
Действительно, перейдем к физическим переменным, получим

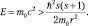(9.16)

Соотношение (9.16) показывает, что если квантовая частица, как «сгусток» энергии движется по законам квантовой механики, то вращательная составляющая движения не должна превышать полную энергию частицы. Поскольку спин частиц ограничен, то в соответствии с неравенством (9.16) получаем область с радиусом r, недоступную для движения частицы («темное пространство»):

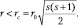
Поскольку внутренний радиус области недоступности движении должен всегда быть меньше внешнего радиуса локализации (формула (9.15)), то получается ограничение на все возможные значения спинов

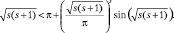(9.18)

Стабильные элементарные частицы с отличной от нуля массой и известным рядом значений спина s = 0, 1/2, 1, 3/2, 2, 5/2 удовлетворяют этому неравенству. Значение s = 5/2 это наибольшее значение удовлетворяющее этому неравенству. Возможно, оно несколько неточно, поскольку используется приближенное решение (9.12).

Таким образом, свободные частицы с ненулевой массой покоя и отличным от нуля спином совершают вращательно-колебательные движения и в основном локализованы в области некого подобия тора. Если у квантовой частицы имеется заряд, то за счет вращательных состояний возникают замкнутые токи и соответствующий магнитный момент, связанный со спином частицы. Решение квантовых уравнений движения в представлении плотности вероятности для частиц с ненулевой массой покоя дает известную последовательность их спинов. Периферийная пространственная структура плотности вероятности зависит от их спинового числа и имеет радиальную область «дрожания». Характерный радиус локализации частиц можно оценить по формуле (9.15). Например, в этой модели область локализации электрона является «пухлой» rsρ = 1,4∙10–10 см по сравнению с областью локализации протона rsρ = 7,4∙10–10 см.

Зная решение этой задачи в представлении плотности вероятности, естественно получить аналогичные результаты и в представлении Шредингера. А именно, необходимо решать уравнение:

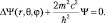(9.19)

Единственное отличие от стандартного решения этого уравнения методом разделения переменных Ψ = Ψr(r)Ψθ(θ)Ψφ(φ) должно заключаться в том, что решение для Ψφ нужно записывать в полном виде:

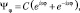(9.20)

поскольку нет предпочтительного направления для вращательных состояний. Это есть «дрожание» для вращательных состояний. Использование одного слагаемого в волновой функции означает, что заведомо задано направление вращения и положение спина в пространстве. Тем не менее, возобладало описание вращательного движения с помощью одного слагаемого в этой формуле, например, для движения электрона в атоме водорода [8]. Использование формулы (9.20) для атома водорода приводит, например, к отличию значений квадрупольных моментов для возбужденных состояний от преж-
них вычислений [9].

Литература

1. Ohania H.C. What is spin? Am. J. Phys. – 1986. V. 54. № 6. P. 500-505.

2. Де Бройль Луи. Избранные научные труды. Т.1. Становление квантовой физики. – М., Логос. 2010. 552 с.

3. Ghosh S.K., Deb B.M. Densities, Density-Functional and Electron Fluids // Physics Reports (Review Section of Physics Letters). – 1982. V. 92, № 1. – P. 1-44.

4. Алексеев Б.В., Абакумов А.И. Об одном подходе к решению уравнения Шредингера // Доклады Академии наук – 1982. Т. 262. – С. 1100-1102.

5. Кузелев М.В.. Рухадзе А.А. О квантовом описании линейных кинетических свойств бесстолкновительной плазмы. УФН, 1999, т. 169, № 6. С. 687-689.

6. Кузелев М.В.. Рухадзе А.А. Нерелятивисткая квантовая теория вынужденных черенковского излучения и комптоновского рассеяния в плазме. ФНТ, 2011, Т.37, № 9/10 С. 1-7.

7. Неволин В.К. Квантовый транспорт в устройствах электроники. – М.: Техносфера, 2012. – 87 с.

8. Ландау Л.Д. и Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. – М., ГизФМЛ. 1963. С. 227.

9. Неволин В.К. Атом водорода: что нового? Наноинженерия 2013. № 2. С. 46.