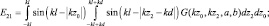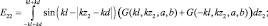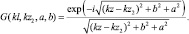Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3. Программа подготовки к работе
1. Изучить теоретические положения, касающиеся нахождения взаимных и собственных сопротивлений электрических вибраторов
2. Уяснить цель и порядок проведения лабораторной работы.
3. Ознакомиться с расчетными соотношениями, провести их анализ.
4. Подготовиться к ответам на контрольные вопросы.
5. Подготовить бланк отчета по работе.
Краткие сведения теории нахождения взаимных и собственных сопротивлений электрических вибраторов
Задача нахождения коэффициентов матрицы сопротивлений возникает при нахождении токов в антенной системе из нескольких излучателей, например, электрических вибраторов. В зависимости от способа возбуждения таких систем различают активные вибраторы, входы которых подсоединены к генераторам, и пассивные вибраторы, возбуждаемые электромагнитным полем других вибраторов. Входы пассивных вибраторов обычно подсоединяют к реактивным нагрузочным сопротивлениям, не вызывающим снижения КПД антенны.
Схема замещения простейшей антенной системы из двух одинаковых параллельных вибраторов, показанной на рис. 1.1, эквивалентным четырехполюсником представлена на рис. 1.2.
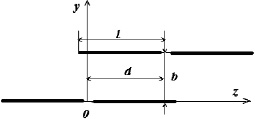
Рис. 1.1. Геометрия задачи
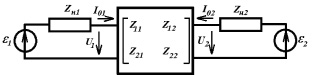
Рис. 1.2. Эквивалентная схема замещения антенной системы из двух коллинеарных электрических вибраторов
Диагональные элементы матрицы сопротивлений представляют собой собственные сопротивления вибраторов, недиагональные – взаимные сопротивления, учитывающие электромагнитную связь между вибраторами.
При не слишком малых расстояниях между тонкими вибраторами можно считать справедливым в первом приближении синусоидальный закон распределения тока вдоль вибраторов:
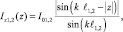(1.1)
где координата z отсчитывается от середины каждого вибратора. Входные токи I01 и I02 определяются из решения системы линейных уравнений Кирхгофа:
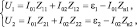(1.2)
в котором ε1, ε2 – эдс возбуждающих генераторов; Zн1, Zн2 – внутренние сопротивления генераторов (в пассивном вибраторе следует полагать ε1 = 0 и считать Zн1 сопротивлением нагрузки).
Для нахождения взаимных сопротивлений вибраторов был предложен приближенный метод наводимых эдс [1–3]. В соответствии с ним в качестве основных расчетных соотношений для определения взаимных и собственных сопротивлений используются выражения вида:
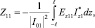(1.3а)
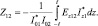(1.3б)
Выражения для Z22 и Z21 = Z12 получаются очевидной заменой индексов. Касательные составляющие Ez11 и Ez12 представляют собой эдс, приходящиеся на единицу длины вдоль боковой поверхности вибратора и порождаемые токами либо первого, либо второго вибратора, что и объясняет название «метод наводимых эдс».
Особенностью рассматриваемого метода является то, что небольшие ошибки в задании закона распределения тока (первого порядка малости) приводят к значительно меньшим ошибкам во взаимных и собственных сопротивлениях (второго порядка малости). Именно этим и объясняется широкое применение метода наводимых эдс в инженерных расчетах вибраторных антенн.
Наилучшие результаты метод дает для взаимных сопротивлений полуволновых резонансных вибраторов, когда распределение тока не зависит от места включения генератора и характера распределения возбуждающей эдс [1]. При численной реализации формулы (1.3а) возникают сложности, обусловленные особенностью функции Грина. Они имеют место при подстановке в указанные выражения соотношения, определяющие касательные составляющие электрического поля на поверхности вибратора и описываемые еще одним интегралом вдоль вибратора. В момент наблюдения точка наблюдения совпадает с точкой источника, и функция Грина за счет своего истокообразного характера обращается в бесконечность. В связи с этим при численной реализации данный момент стараются выделить и представить в замкнутой форме, например, с помощью метода Стреттона-Чу [3].
В ходе лабораторной работы рассмотрим два способа получения оценок коэффициентов взаимной связи полуволновых вибраторов:
– с использованием аппроксимационных полиномов, предложенных в работе [1];
– с использованием аналитических выражений, приведенных в работе [3].
В первом случае для вибраторов с соотношением длины вибратора к его радиусу la и длиной плеча l собственное сопротивление вычисляется с использованием формул [1]:
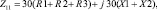(1.4)
где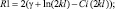 
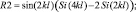
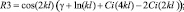
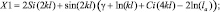
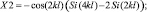
γ = 0,5772157 – число Эйлера.
Входящие в соотношения (1.4) функци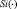и 
и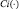 
являются синус- и косинус-интегралами и могут быть найдены с использованием аппроксимационных выражений [4]:
– при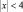 
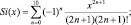(1.5а)
– при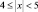 
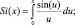(1.5б)
– при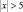 
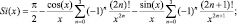(1.5в)
– при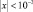 
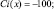(1.6а)
– при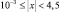 
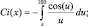(1.6б)
– при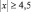 
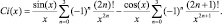(1.6в)
При использовании метода Стреттона-Чу коэффициент взаимного сопротивления определяется по формуле [3]:
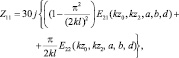(1.7)
где 
