
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.4. Описание порядка работы
Работа выполняется в следующей последовательности.
1. Вычисление значений собственного сопротивления вибратора с соотношением la = 10–6 с использованием программы Взаимная связь вибраторов .xmcd и ЛР1.xmcd, тексты которых приводятся в приложениях А и Б к данному разделу, для двух значений длины: l = 0,25λ и l = 0,5λ. В первой программе реализуется метод Стреттона-Чу, во второй применяется аппроксимационная формула из [1].
Занесение полученных результатов в отчет в виде табл. 1.1 и сравнение с известными из теории значениями активной и реактивной составляющих.
Таблица 1.1
Оценка точности получаемых результатов путем сравнения с известными
|
l = 0,25λ Результаты натурного эксперимента: R = Ом, X = Ом |
l = 0,5λ Результаты натруного эксперимента: R = Ом, X = Ом |
|||
|
Результаты |
Результаты |
|||
|
R |
X |
R |
X |
|
|
Аппроксимационная формула |
||||
|
Метод Стреттона-Чу |
||||
2. Исследование влияния параметров вибратора (длины плеча и толщины) на величину активной и реактивной составляющих величины собственного сопротивления вибратора.
Изменяя длину вибратора в интервале от l = 0,22λ до l = 0,25λ с шагом 0,001λ построить графики зависимости величины активной и реактивной составляющих собственного сопротивления для двух значений радиуса вибратора a = 3∙10–4 и a = 10–2. Сделать выводы по результатам полученных графиков. Графики привести в отчет.
3. С использованием программы ЛР1.xmcd построить графики зависимостей активной и реактивной составляющих взаимного сопротивления двух полуволновых вибраторов, разнесенных
– в осевом направлении в интервале от 0 до 1,5λ;
– в поперечном направлении от 0 до 1 λ.
В обоих случаях дискрет изменения значений расстояний составляет 0,25λ. Вычислить резонансную длину вибратора (длина, при которой реактивная составляющая собственного сопротивления обращается в нуль).
Сравнить полученные значения с данными натурных экспериментов из [5], которые приведены в приложении В к данному разделу.
4. С использованием метода зеркальных изображений вычислить собственное сопротивление горизонтального полуволнового вибратора при удалении h его от идеально проводящего экрана на расстояние:
– 0,125λ;
– 0,25λ;
– 0,5λ.
Нарисовать геометрию задачи и сравнить полученные значения с табличными.
Методические указания по вычислению:
– вычислить собственное сопротивление излучателя в свободном пространстве. Допустим R и X;
– с использованием метода зеркальных изображений влияние экрана заменяется на фиктивный излучатель, расположенный на удалении 2h от истинного излучателя, как показано на рис. 3. Влияние границы раздела сред (металлический экран) учитывается комплексной амплитудой тока (по вычисленному значению коэффициента отражения Френеля) [3].
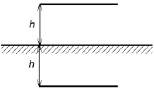
Рис. 1.3. Геометрия задачи нахождения собственного сопротивления излучателя вблизи металлического экрана методом зеркальных изображений
Вычисляется или находится из таблицы, приведенной в приложении В, величина взаимного сопротивления при смещении излучателя в направлении b/λ = 2h, т.е. значения R1 и X1;
– поскольку коэффициент отражения для горизонтального электрического вибратора вблизи металлического экрана равен RE = –1,
то величина собственного сопротивления вибратора будет определяться как суперпозиция двух составляющих по формуле:
Z = (R – R1) + j(X – X1). (1.8)
5. Анализ полученных результатов, оформление выводов и отчета по проведенной работе.
