Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

4.3. Фрактальные модели ингибирования термоокислительной деструкции для модифицированного ПЭВП

Общим положением, установленным авторами [33; 34] в рамках фрактального анализа, является то, что повышение стабильности структуры относительно воздействия температуры всегда оказывает положительное влияние на процесс структурной стабилизации термоокислительной деструкции. Аналогичный вывод сделан авторами [35] для полимерных расплавов.

Как отмечалось в главе 1, структура твердофазных полимеров и полимерных расплавов является фракталом в интервале линейных масштабов от нескольких ангстрем до нескольких десятков ангстрем. Именно в этот интервал попадают размеры полостей свободного объема, через которые реализуется диффузия оксидантов (особенно газообразных, например, кислорода) к реакционноспособным центрам полимерных макромолекул. Как показано в главе 2, законы, описывающие перенос на фрактальных объектах (аномальный или странный перенос), принципиально отличаются от соответствующих законов для евклидовых объектов. В связи с этим приведем два примера. Если траекторию молекулы газообразного диффузанта рассматривать как случайное блуждание со среднеквадратичным шагом x, то число таких шагов N_w определяется соотношением [36]:

,                                                           (4.8)

где d_w - размерность траектории случайного блуждания.

Для евклидовых пространств d_w = 2 независимо от их размерности, тогда как для фракталов эта размерность существенно больше 2 [36]. Таким образом, число шагов N_w при одинаковых x для фрактала будет гораздо больше, чем для евклидова объекта. Иначе говоря, на фрактальном объекте молекуле диффузанта (оксиданта) потребуется сделать гораздо больше шагов для достижения реакционноспособного центра полимерной макромолекулы, что должно привести к изменению кинетики термоокислительной деструкции.

Число посещенных случайным блужданием мест  определяется следующим образом [36]:

,                                                        (4.9)

где d_s - спектральная размерность, характеризующая связности объекта [37].

Для евклидовых объектов с размерностью 3 d_s = 3, тогда как для фрактальных объектов d_s < 2 [36]. Из соотношения (4.9) следует, что число посещенных случайным блужданием мест во фрактальном пространстве будет гораздо меньше, чем в евклидовом. Применительно к вопросу термоокислительной деструкции это означает, что в первом случае молекула оксиданта сможет контактировать с гораздо большим числом реакционноспособных центров полимерной макромолекулы, чем во втором. Поэтому мы ожидаем, что скорость термоокислительной деструкции для фрактальных твердофазных полимеров будет заметно ниже предполагаемой для евклидовых твердых тел [38].

В работах [39; 40] было показано, что структура твердофазных полимеров моделируется совокупностью большого числа кластеров Виттена-Сандера (кластеров WS, см. главу 1). Процессы переноса и реакции на таких кластерах подробно рассмотрены в работе [41]. Как отмечалось в предыдущем разделе, стабилизация ПЭВП высокодисперсной смесью Fe/FeO (Z) приводит к ослаблению термоокислительной деструкции при температурах как ниже, так и выше температуры плавления Т_пл полиэтиленов. По своей физической сущности частицы Z играют роль захватов для молекул оксиданта (кислорода) и, кроме того, Z является модификатором структуры ПЭВП, что особенно ярко выражено при содержании Z 0,05 вес. %. Теоретическая трактовка указанных эффектов на кластерах WS также дана в работе [41]. По отношению к механизму стабилизации полиэтиленов Z возникает ряд вопросов, которые можно сформулировать следующим образом. Во-первых, представляет интерес дополнительное исследование очень сильного стабилизирующего действия Z при его содержании ~ 0,05 вес. % Z (рис. 4.11). Во-вторых, возникает вопрос об очень различающихся скоростях термоокислительной деструкции в твердофазном полимере и его расплаве (на 2 ¸ 3 порядка) [38]. И наконец, существует проблема сохранения сильного стабилизирующего действия Z при содержании его ~ 0,05 вес. % в расплаве полиэтиленов [6]. Авторы [38] дали ответ на поставленные выше вопросы в рамках фрактального анализа (кластер WS является фракталом с размерностью ~ 2,5 [36]).

В работе [41] рассмотрена теоретическая трактовка захвата случайного блуждания (молекулы кислорода) ловушками (частицами Z) на фрактальном объекте. Средняя вероятность выживания случайного блуждания F(t) определяется следующим соотношением [41]:

F(t) ~ exp(-с₃р^bt^g),                                            (4.10)

где с₃ - константа; р - концентрация ловушек; t - время, а показатели b и g определены так [41]:

,                                                         (4.11)

b = 1 - g.                                                              (4.12)

Следуя модели нецепного ингибирования [2], авторы [38] предположили, что стабилизирующее действие Z сохраняется до тех пор, пока вероятность выживания F(t) молекул кислорода очень мала, т.е., пока практически весь кислород захватывается ловушками (частицами Z). Такая трактовка согласуется с экспериментальными данными, полученными при тепловом старении композиций ПЭВП + Z. Эти результаты показывают неизменность исследуемого свойства (например, А_р или ПТР, см. рис. 4.11) в течение некоторого промежутка времени старения t_ст, после чего начинается достаточно резкое изменение этого свойства [6; 20]. Таким образом, предположив для F(t) произвольную достаточно малую (близкую к нулю) величину, например,0,03, можно из соотношения (4.10) оценить величину t_ст, на протяжении которого сохраняется условие F(t) » 0,03.

Технически эта задача требует определения спектральной размерности d_s. После чего, используя уравнение (4.9), можно определить величину  в предположении, что эта величина обратно пропорциональна продолжительности участка старения , на котором Z сохраняет свойства нецепного ингибитора.

Рассмотрим вопрос оценки d_s. Такую оценку легко выполнить, зная фрактальную размерность структуры полимера d_f или принять ее постоянной, равной величине спектральной размерности для кластера WS [36]. Однако процессы теплового старения протекают при достаточно высоких температурах, близких или превышающих Т_пл полимера. Как показано в работах [42; 43], в таких условиях поведение полимера определяет эффективная спектральная размерность  , что соответствует теореме о субординации (уравнение (1.70)). Поскольку параметр b¢ в указанном уравнении трудно определить экспериментально [43], то авторы [38] определили  из экспериментальных данных по изменению какого-либо  из указанных выше свойств при старении. Если скорость изменения этого свойства k подчиняется временной зависимости, выражаемой уравнением (1.68), то это означает фракталоподобное поведение в процессе старения и величина  определяется из уравнения (1.69).

Как следует из графиков изменения свойств композиций ПЭВП + Z [6; 20], очень быстрый спад наблюдается для всех композиций ПЭВП + Z, за исключением композиции с содержанием Z 0,05 вес. %. Это означает, что величина  для последней из указанных композиций гораздо ниже, чем для остальных. Количественные оценки дали такие результаты:  = 1,20 для композиции ПЭВП + Z с содержанием Z 0,05 вес. % и  = 1,80 для остальных композиций ПЭВП+Z. Расчет величин согласно изложенной выше методике и сравнение их с экспериментальными значениями  (рис. 4.14) показало хорошее соответствие, что подтверждает корректность предложенной трактовки [38].

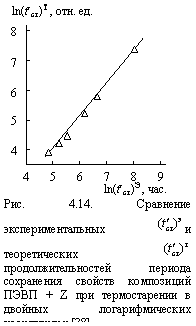
Как показало сравнение экспериментальных данных при тепловом старении ниже (353 К) и выше (463 К) температуры плавления, величины в первом случае имеют порядок 10³ час, а во втором - нескольких часов, т.е., наблюдается различие до трех порядков величины. Это различие легко объясняется в рамках предложенной модели, если учесть, что в первом случае процессы теплового старения протекают во фрактальном, а во втором - в евклидовом (или близком к евклидовому) пространствах [44]. Как известно [41], для евклидовых объектов d_s = d, т.е., в рассматриваемом случае d_s = 3. Сочетание уравнений (4.9) и (4.10) позволяет получить следующее соотношение для оценки [38]:

.                                                     (4.13)

При с₃ = const и указанных выше значениях  в случае композиции ПЭВП + Z с содержанием Z 1,0 вес. % получим » 10² во фрактальном и » 10⁵ - в евклидовом пространствах. Соответственно времена  составят ~ 10^-2 в первом и ~ 10^-5 - во втором случае. Легко видеть, что эта простая оценка дает то же различие в три порядка, что и экспериментальные данные [38].

Таким образом, применение модели Виттена-Сандера и фрактального анализа позволяет выяснить основные особенности поведения композиций ПЭВП + Z в процессе теплового старения и выполнить полуколичественную оценку этих эффектов. Особенно важно отметить очень большое различие скоростей термоокислительной деструкции на фрактальных и евклидовых объектах. По существу, трактовка [38] является фрактальным описанием структурной стабилизации полимеров [31].

Как отмечалось выше, в процессах термоокислительной деструкции аморфно-кристаллических полимеров большую роль играет пространственная неоднородность, т.е., как структурные особенности самого полимера, так и размеры и распределение частиц акцептора кислорода. Наличие пространственного беспорядка приводит к появлению временного, а часто и энергетического беспорядка [43; 45]. Появление временного беспорядка играет важную роль в процессах термоокислительной деструкции, поскольку эти процессы, как правило, имеют довольно большую продолжительность [20]. Такую сложную ситуацию невозможно исследовать аналитически и необходимо применение специальных моделей, каким является фрактальный анализ [45]. Авторы [46] выполнили более подробное исследование различия величин периодов индукции  при температурах выше и ниже Т_пл, используя как модель [41], так и фрактальную модель протекания химических реакций в неупорядоченных средах [45].

На рис. 4.15 и 4.16 приведены зависимости относительного тангенса угла диэлектрических потерь tgd/tgd₀ от продолжительности теплового старения t_ст при температурах старения Т_ст = 353 и 463 К, соответственно. В качестве tgd принят текущий тангенс угла диэлектрических потерь после определенных промежутков старения t_ст, а в качестве tgd₀ - cоответствующая величина для исходного образца при t_ст = 0. Обращает на себя внимание симбатность зависимостей tgd/tgd₀(t_ст) при обеих указанных температурах старения, где образцы по величине периода индукции  выстраиваются в следующем порядке (по возрастанию ): ПЭВП и композиции ПЭВП + Z с содержанием Z 1,0; 0,1 и 0,05 вес. %. По существу, единственным различием является порядок величины : при Т_ст = 353 К  = 10 ¸ 10³ час, при Т_ст = 463 К  = 1,0 ¸ 3,8 час. Такое соотношение позволяет предложить единый механизм термоокислительной деструкции, а различие абсолютных величин   отнести за счет радикальных структурных изменений при переходе от аморфно-кристаллического состояния (при 353 К) к вязкотеку4чему (при 463 К) [46].

Симбатность зависимостей tgd/tgd₀(t_ст) позволяет получить простую корреляцию величин  при 353 и 463 К (( )₃₅₃ и ( )₄₆₃, соответственно). На рис. 4.17 приведено соотношение этих периодов индукции для исследуемых полиэтиленов, которое имеет следующую аналитическую форму:

.                                            (4.14)

По существу, изменение скорости термоокислительной дестуркции, выражаемой величиной , можно рассматривать как изменение порядка реакции от первого (при 353 К) до пятого (при 463 К) [46].

Описать процесс ингибирования кислорода частицами акцептора Z можно исследованием следующего типа псевдомономолекулярной реакции (задача о мишени) [45]:

A + B → B,                                                         (4.15)

где реагент А подвижен (кислород), а подвижность реагента В(Z) равна нулю.

В этом случае спадание способности Z ингибировать термоокислительную деструкцию F^АВ подчиняется следующему уравнению [45]:

,      (4.16)

где С₄ - константа; g_в - показатель временного беспорядка.

Как и ранее, полагаем, что исчерпание ингибирующей способности Z означает окончание периода индукции и начало интенсивной термоокислительной деструкции, что отчетливо видно на рис. 4.15 и 4.16, где начало деструкции указано резким ростом tgd/tgd₀. Полагая, как и выше, в этом случае F^АВ = 0,03, t_ст = ( )₄₆₃ и d_s = 1, поскольку ПЭВП является линейным полимером [37], можно рассчитать константу С₄ в уравнении (4.16) с учетом следующего условия [46]:

g_в = n,                                                                   (4.17)

где n - порядок реакции, принимаемый для Т_ст = 463 К равным 5.

Таблица 4.4

Сравнение экспериментальных и теоретических параметров процесса теплового старения для композиций ПЭВП + Z [46]

Содержание Z, вес. %	, час.	, час.	Р, вес. %
0	8,0	2,5	-
0,05	890	790	0,053
0,10	90	80	0,106
1,0	120	144	0,916

Условие (4.17) было выбрано авторами [46] в качестве гипотезы и его доказательство будет приведено ниже. Затем из уравнения (4.16) можно рассчитать величину ( )₃₅₃ при тех же условиях и с оцененной ранее константой С₄, но (с учетом условия (4.17)) g_в = 1. Сравнение рассчитанных таким образом теоретических величин ) и полученных экспериментально из данных рис. 4.15  приведено в табл. 4.4, откуда следует их хорошее соответствие.

Теперь рассмотрим теоретическое подтверждение априорного условия (4.17). При условии одинакового числа посещаемых случайным блужданием с непрерывным временем (СБНВ), которым моделируется траектория молекулы кислорода, мест  (а это условие следует из одинаковой величины F^АВ = 0,03 при обеих температурах старения) получим [45]:

.                                             (4.18)

Произвольно полагая = const = 1000, получим величины g_в для обеих температур старения в случае трех исследуемых композиций ПЭВП + Z. Из приведенного на рис. 4.18 соотношения рассчитанных таким образом величин g_в можно видеть, что для них практически точно выполняется отношение 5 : 1, т.е., отношение порядков реакции. С практической точки зрения это предполагает, что выполнение испытаний на тепловое старение при Т_ст = 463 К, которое протекает очень быстро, позволяет заменить гораздо более длительные испытания при Т_ст = 353 К.

Далее рассмотрим эффективность Z при обеих указанных температурах, используя следующее соотношение [45]:

,              (4.19)

где С₅ - константа; р - концентрация ловушек.

Рассчитав величину С₅ при Т_ст = 353 К, можно рассчитать величину р при Т_ст = 463 К, используя эту же величину С₅. Сравнение концентрации Z и величин р также приведено в табл. 4.4, откуда следует их примерно равенство (расчет р проводится с учетом разных величин g_в для Т_ст = 353 К и 463 К). Это означает, что эффективность Z одинакова в аморфно-кристаллическом и вязкотекучем состояниях, а различие величин ( )₃₅₃ и ( )₄₅₃ обусловлено структурными особенностями указанных состояний, в частности, гораздо более высоким коэффициентом диффузии по кислороду для второго [47; 48].

Следовательно, применение методов фрактального анализ для описания процессов теплового старения композиций ПЭВП + Z позволило выяснить следующие аспекты этой проблемы. Порядок реакции ингибирования термоокислительной деструкции акцептором кислорода Z определяется уровнем временного (и, возможно, энергетического) беспорядка структуры. Это обстоятельство позволяет прогнозировать период индукции ( )₃₅₃ при Т_ст = 353 К по известным значениям аналогичного параметра при Т_ст = 463 К. Это означает также, что процесс ингибирования при Т_ст = 463 К подчиняется теореме о субординации, т.е., наблюдается мультипликативное поведение показателей, характеризующих пространственный и временной беспорядок. Эффективность Z в качестве акцептора кислорода одинакова при обеих использованных температурах старения [46].

Структурный аспект эффективности использования Z (S_t) в качестве акцептора кислорода рассмотрен в работе [49]. В настоящее время существует ряд количественных критериев для оценки величины S_t в случае нецепного ингибирования [1; 20]. Например, один из таких критериев имеет вид [1]:

,                                                                              (4.20)

где t и t¢ - время, в течение которого стабилизированный и нестабилизированный полимеры сохраняют необходимый эксплуатационный уровень конкретного физико-химического параметра.

Как отмечалось выше, теоретическую оценку величины t позволяет уравнение (4.7), в котором величины и [O₂]₀ связаны между собой следующим соотношением [50]:

,                                                     (4.21)

где  - проницаемость полимера по кислороду.

С учетом соотношения (4.21) уравнение (4.7) можно записать так [49]:

.                                              (4.22)

Однако приведенные выше результаты продемонстрировали, что уравнения (4.7) или (4.22) не всегда адекватны при описании экспериментальных значений t даже с учетом происходящих структурных изменений, учитываемых параметрами и [O₂)₀ или . Наиболее типичным в этом смысле является сравнение композиций ПЭВП + Z, содержащих 0,05 и 1,0 вес. % Z. Для первой из указанных композиций величина [Z] в 20 раз меньше, чем для второй, а величина примерно на порядок ниже (см. табл. 4.1) Тогда соотношение (4.22) предсказывает, что t для композиции ПЭВП + Z с содержанием Z 1,0 вес. % должно быть примерно в 2 раза больше соответствующего параметра для ПЭВП + Z, содержащей 0,05 вес. % Z. Однако экспериментальные данные показали противоположную тенденцию (см. рис. 4.11). Это предполагает наличие некоторых структурных факторов, не учитываемых уравнениями (4.7) или (4.22). Поэтому авторы [49] предприняли попытку выяснения этих факторов и уточнили уравнение (4.22) с целью устранения указанной выше неадекватности.

Рассмотрим теоретический расчет t по уравнению (4.22) для трех исследуемых композиций ПЭВП + Z . Некоторые экспериментально оцененные характеристики этих композиций приведены в табл. 4.5. Были приняты следующие значения постоянных величин: С₂ = 6,25 ´ 10^-3, t¢ = 200 час. Рассчитанные t^т и экспериментальные t^э (оцененные по изменению ударной вязкости А_р при температуре старения 353 К [6]) величины периода индукции приведены в табл. 4.5. Если для композиций с содержанием Z 0,05 и 0,10 вес. % получено достаточно хорошее соответствие теории и эксперимента, то при содержании Z 1,0 вес. % величина t^т примерно в 7 раз превышает t^э [49].

Таблица 4.5

Структурные характеристики и свойства композиций  ПЭВП + Z [49]

Содержание Z, вес. %	Rср, нм	´ 1017 [2],	tэ, час	tт, уравнение (4.22), час
0,05	37	0,16	1180	1230
0,10	55	0,80	480	493
1,0	55	1,70	390	2335

Авторы [49] рассмотрели возможные причины указанного несоответствия с учетом структуры частиц Z. На рис. 4.8 показана зависимость среднего радиуса частиц Z R_ср от содержания Z C_Z, из которой следует резкое изменение величины R_ср при С_Z » 0,10 вес. %, а на рис. 4.7 приведена электронная микрофотография скола образца композиции ПЭВП + Z, из которой видно, что частицы Z имеют разные размеры и структуру. При этом небольшие частицы с радиусом R_ср » 50 ¸ 100 нм имеют округленную форму и гладкую поверхность, тогда как поверхность больших частиц очень шероховата и предположительно имеет фрактальную структуру. Это позволяет предположить, что большие частицы представляют собой фрактальные агрегаты, формирующиеся из мелких частиц Z. Очевидно, что показанное на рис. 4.8 дискретное изменение R_ср при C_Z » 0,10 вес. % обусловлено этим процессом агрегации вследствие роста C_Z.

Полагая, что частицы Z имеют сферическую форму, можно рассчитать их объем по известным значениям R_ср (рис. 4.8) и затем получить число частиц N_Z на единицу объема композиций ПЭВП в относительных единицах, которое приведено в табл. 4.6. Расчет размерности d_п поверхности частиц Z можно выполнить следующим образом. Для гладких частиц d_п = 2, а для шероховатых (предположительно фрактальных) поверхностей величина d_п рассчитана по контуру проекции частицы на поверхности скола, показанной на рис. 4.7, хорошо известным методом ячеек [51; 52]. Увеличенная микрофотография границы частицы Z покрывалась сеткой квадратов с размером ячейки r_i, варьирующимся в пределах 4,5 ¸ 24 мм с постоянным отношением r_i/r_i+1 = 1,5, и затем подсчитывалось число квадратов N_i, через которые проходит или которых касается контур границы Z. Для каждого измерения выбиралось пять произвольных положений сетки относительно микрофотографии. Если граница частицы Z является фрактальной кривой, то должно выполняться соотношение [51; 52]:

.                                                           (4.23)

Таблица 4.6

Расчетные параметры фрактальной модели [49]

Содержание Z, вес. %	dп3	du	NZ, отн. ед.	М4, отн. ед.	М4 ´ NZ, отн. ед.	tт, уравнение (4. ), час.
0,05	2,0	2,0	2,89	1,37´103	3,96´104	945
0,10	2,0	2,0	2,79	3,03´103	8,45´104	518
1,0	2,64	1,764	15,70	1,09´103	17´104	500

На рис. 4.19 приведена зависимость N_i(r_i), соответствующая соотношению (4.23), в двойных логарифмических координатах для одной из частиц, показанных на рис. 4.7, чей контур границы показан в правом верхнем углу рис. 4.19. Как можно видеть, получена ожидаемая линейная корреляция, позволяющая определить по ее наклону величину d_п. После расчета по соотношению (4.23) была получена величина d_п = 1,26 для проекции на плоскость (двухмерное евклидово пространство). Для получения фрактальной размерности этой же границы в трехмерном евклидовом пространстве d_п3 производился перерасчет полученной рассмотренным выше способом величины d_п по формуле [53]:

,                               (4.24)

где d - размерность евклидова пространства, для которого ведется расчет (в нашем случае d = 3).

Рассчитанная по уравнению (4.24) величина d_п3 равна 2,64. В первом приближении была принята фрактальная размерность агрегата частиц Z D_Z, равная d_п3, т.е., D_Z = 2,64 [49].

Чтобы гарантировать корректность расчета фрактальной размерности объекта (в нашем случае - поверхности частицы Z), недостаточно условия d_п3>2, где d = 2 для поверхности частицы. Необходимо также подтвердить самоподобие объекта и определить интервал масштабов его фрактального поведения, поскольку частица Z является физическим (а не математическим) фракталом [54]. Для самоподобных фрактальных кривых, подобных описанной выше, должно выполняться условие (при r_i/r_i+1 = const) [55]:

.                                                (4.25)

На рис. 4.20 приведена зависимость, соответствующая соотношению (4.25), для указанной на рис. 4.19 частицы Z. Как можно видеть, эта зависимость линейна, проходит через начало координат и согласно соотношению (4.25) подтверждает самоподобие поверхности (и, следовательно, агрегата) частицы Z. Очевидно, что это самоподобие будет статистическим. Минимальный интервал самоподобия равен интервалу использованных r_i, т.е., 4,5 ¸ 24 мм или, с учетом увеличения микрофотографии рис. 4.7, ~ 0,6 ¸ 3,2 мкм.

Размерность неэкранированной, т.е., доступной для реакции, поверхности d_u можно определить согласно уравнению [56]:

d_u = (D_Z - 1) + (d - D_Z)/d_w,                               (4.26)

где d_w - размерность траектории случайного блуждания на фрактале, равная ~ 3,4 [36].

Для частицы небольшого размера с D_Z = d = 3 из уравнения (4.26) получим d_u = 2, т.е., вся поверхность доступна для реакции. Для фрактальных частиц с D_Z = 2,64 d_u = 1,764. Число неэкранированных мест поверхности M_u масштабируется с радиусом частицы R_ср так [56]:

                        (4.27)

Расчет по соотношению (4.27) дает величины M_u в относительных единицах, которые приведены в табл. 4.6. Данные этой таблицы показывают, что увеличение Rс_р при одинаковых d_u (композиции ПЭВП + Z с содержанием Z 0,05 и 0,10 вес. %) приводит к росту M_u, а уменьшение размерности d_u от 2 до 1,764 при одинаковых R_ср (композиции с содержанием Z 0,10 и 1,0 вес. %) приводит к резкому (более чем в 3 раза) снижению M_u. Умножив M_u на N_Z, получим произведение M_u ´ N_Z, характеризующее эффективность Z в качестве стабилизатора (табл. 4.6), тогда как изменение коэффициента газопроницаемости  (табл. 4.5) характеризует эффективность Z в качестве модификатора структуры. Совместное действие этих эффектов определяет итоговую эффективность Z, которую можно выразить следующим образом, используя те же параметры, что и в уравнениях (4.7), (4.20) и (4.22) [49].

.                                   (4.28)

Расчет t по уравнению (4.28) с С₆ = 1,875 и t¢ = 200 час дает теоретические значения t^т, гораздо лучше согласующиеся с экспериментом, чем расчет по исходному уравнению (4.22) табл. 4.6). Отметим, что во всех случаях расчет проводился для диффузионного режима термоокислительной деструкции, поскольку l = 4 мм, т.е., больше 1 мм [1]. Расхождение между величинами t, определенными экспериментально [6] и рассчитанными по уравнению (4.28), может достигать 20 % и его причины достаточно очевидны. К таковым следует отнести экспериментальную оценку t только по одному параметру А_р и дискретность оценки этой величины, использование d_п только для одной частицы и т.д. Поэтому максимальная погрешность 20 % может считаться хорошим соответствием теории и эксперимента. В качестве примера отметим, что оценка экспериментальных величин t по изменению тангенса угла диэлектрических потерь образцов после теплового старения (рис. 4.15 и 4.16) даст другие значения и t^э, и t^т за счет изменения t¢ в уравнениях (4.7) и (4.22) [49].

Следовательно, учет структуры частиц Z позволяет значительно улучшить соответствие экспериментальных и теоретических значений t, по крайней мере, для композиции ПЭВП + Z, содержащей 1,0 вес. % Z. Как следует из сравнения данных табл. 4.5 и 4.6, наибольшую интегральную эффективность Z проявляет при концентрации 0,05 вес. %, что в основном обусловлено его сильным модифицирующим действием (резким снижением ). Отметим, что резкое снижение эффективности действия Z при концентрации 1,0 вес. % обусловлено как разрыхлением структуры (относительно высокие значения ), так и сильным экранирующим эффектом фрактальной поверхности частиц Z [49].