Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

5.2. Структурная трактовка термоокислительной деструкции твердофазных аморфнокристаллических полимеров

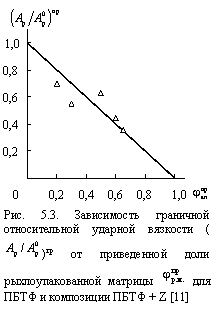
В работах [9; 10] было показано, что зависимости относительной ударной вязкости от продолжительности теплового старения t_ст для ПБТФ + Z распадаются на три участка (для исходного ПБТФ - на два участка), которые показаны для ПБТФ и двух композиций ПБТФ + Z на рис. 4.21 и 4.22, соответственно. Применение фрактального анализа позволило выяснить физические причины такого поведения функции  и дать химические механизмы термоокислительной деструкции для каждого из участков (см. раздел 4.4 предыдущей главы). Однако, из графиков рис. 4.21 и 4.22 следует, что для ПБТФ и композиций ПБТФ + Z с разным содержанием Z участок с наиболее быстрым спадом  по мере роста t_ст (и, следовательно, нежелательный в практических приложениях ПБТФ) прекращается при разных значениях  , после чего начинается гораздо более медленный спад , т.е., более предпочтительный с практической точки зрения. Авторы [11; 12] выяснили причины такого поведения зависимости  для ПБТФ и композиций ПБТФ + Z, а также получили рекомендации, позволяющие сокращение или подавление участка наиболее быстрого спада указанной функции.

Рассмотрим зависимости , приведенные на рис. 4.21 и 4.22, несколько подробнее. На первом участке этих зависимостей для композиций ПБТФ + Z, характеризуемом условием = const = 1,0, реализуется ингибированная термоокислительная деструкция, описываемая в рамках задачи о ловушках [13]. Отсутствие ингибитора термоокислительной деструкции в исходном ПБТФ приводит к отсутствию для него указанного участка. Как отмечалось в предыдущей главе, смесь Fe/FeO является также сильным модификатором структуры, приводящим к экстремальному росту относительной доли кластеров j_кл при содержании Z C_Z » 0,05 ¸ 0,10 вес. % и соответствующему росту протяженности первого участка (периода индукции)  . Кроме того, было установлено (см. раздел 4.4 предыдущей главы), что на втором участке зависимости реализуется псевдомономолекуляррная реакция (реакция промежуточных продуктов распада с макромолекулой полимера), а на третьем (втором для ПБТФ) - бимолекулярная реакция (реакция кислорода с макромолекулой) [9].

Из более внимательного рассмотрения графиков рис. 4.22 можно сделать вывод, что увеличение  сопровождается прекращением псевдомономолекулярной реакции при более высоких значениях , т.е., ослаблением эффекта данной реакции. Как отмечалось выше, увеличение   обусловлено экстремальным ростом j_кл в интервале С_Z = 0,05 ¸ 0,10 вес. % и соответствующим ослаблением диффузии кислорода в некристаллические области полимера. Поскольку модифицирующее действие Z сохраняется и после исчерпания его ингибирующего действия, то отмеченное выше соответствие между величиной  и значением , при котором происходит переход от псевдомоно- к бимолекулярной реакции, обусловлено теми же эффектами структурной стабилизации. Сокращение участка псевдомономолекулярной реакции по мере роста   позволяет сделать предположение, что указанная реакция протекает в наименее плотноупакованных областях полимера. В рамках кластерной модели показано [12], что структура аморфно-кристаллического полимера состоит из двух фаз - аморфной и кристаллической, а первая из указанных фаз состоит из кластеров и рыхлоупакованной матрицы. Относительную долю рыхлоупакованной матрицы j_р.м. можно определить из соотношения (2.33. В свою очередь, величина j_р.м. в расчете на весь полимер (приведенная величина ) определяется так [14]:

.                                                     (5.1)

На рис. 5.3 показана зависимость величин , соответствующих переходу от псевдомоно- к бимолекулярной реакции термоокислительной деструкции от . Как следует из данных этого рисунка, получен результат, подтверждающий сделанное выше предположение - увеличение  приводит к уменьшению граничной величины относительной ударной вязкости ( )^гр и увеличению протяженности участка действия псевдомономолекулярной реакции, которую можно записать как 1 - ( )^гр. При отсутствии рыхлоупакованных областей, т.е., j_кл + К = 1, ( )^гр = 1 и указанная реакция протекать не может - ее продолжительность равна нулю. При = 1,0 эта реакция является единственной в процессе термоокислительной деструкции и продолжается до реализации условия А_р = 0 [11].

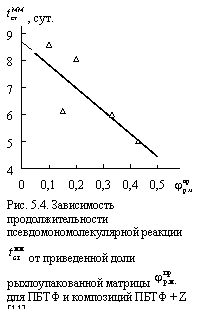
Из сказанного выше можно сделать еще одно предположение, а именно, что увеличение  должно снижать продолжительность действия псевдомономолекулярной реакции. Действительно, приведенная на рис. 5.4 зависимость продолжительности этой реакции  от  подтверждает это предположение. При = 0  » 8,7 сут., т.е., для исходного ПБТФ это время является периодом индукции, а затем происходит переход к бимолекулярной реакции. Экстраполяция графика ( ) к  = 1,0 дает, как и следовало ожидать = 0. Это означает, что в указанных условиях псевдомономолекулярная реакция протекает очень быстро. Подтверждение этого вывода можно получить из результатов теплового старения ПБТФ при температурах выше его температуры плавления, т.е., теплового старения его расплава, где К = 0 и j_кл = 0 и, следовательно, из уравнения (2.33) j_р.м. = = 1,0. В этом случае процесс термоокислительной деструкции полностью завершается (полимер практически теряет свою вязкость) за период менее одного часа, что во временном масштабе рис. 5.4 практически означает » 0.

Можно предположить следующую причину протекания псевдомономолекулярной реакции именно в рыхлоупакованных областях ПБТФ и композиций ПБТФ + Z. Грубо говоря, псевдомономолекулярная реакция предполагает взаимодействие двух полимерных макромолекул в процессе термодеструкции, а это означает необходимость определенной степени молекулярной подвижности, обеспечивающей указанное взаимодействие. Как известно [15], отличная от нуля молекулярная подвижность может быть реализована только в рыхлоупакованных областях аморфно-кристаллических полимеров.

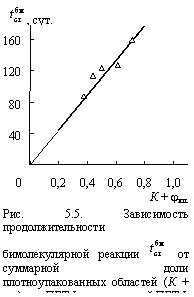
Логическим следствием рассмотренного выше структурного механизма псевдомономолекулярной реакции является предположение, что бимолекулярная реакция представляет собой термоокислительную деструкцию плотноупакованных областей полимера (кристаллитов и кластеров) и именно это обстоятельство определяет резкое снижение скорости ее протекания по сравнению со скоростью псевдомономолекулярной реакции. Чтобы подтвердить это положение, авторы [11] определили продолжительность бимолекулярной реакции экстраполяцией зависимости  к А_р = 0. Зависимость полученной таким образом величины  от суммарной относительной доли плотноупакованных областей (кристаллитов и кластеров) (К + j_кл) приведена на рис. 5.5. Как следует из данных этого рисунка, наблюдается линейный рост  по мере увеличения (К + j_кл) и при (К + j_кл) = 0 величина  также равна нулю. Это означает, что в отсутствие плотноупакованных областей бимолекулярная реакция не имеет места. Этот вывод подтверждается результатами теплового старения расплава ПБТФ, где термоокислительная деструкция полностью реализуется в рамках псевдомономолекулярной реакции.

Следовательно, изложенные выше результаты показали, что химические механизмы термоокислительной деструкции ПБТФ и композиций ПБТФ + Z определяются их структурными характеристиками. Псевдомономолекулярная реакция реализуется только в рыхлоупакованных областях этих аморфно-кристаллических полимеров, а бимолекулярная - только в плотноупакованных. Это указывает, что эффект структурной стабилизации важен на любом участке процесса термоокислительной деструкции. Для подавления наиболее нежелательной с практической точки зрения псевдомономолекулярной реакции существуют да способа. Первый из них (физический) требует создания полностью плотноупакованной структуры полимера, что является достаточно сложной задачей [16]. Второй (химический) требует разработки комплексного стабилизатора, который при его совместном со смесью Fe/FeO введении в ПБТФ был бы способен нейтрализовать действие псевдомономолекулярной реакции.

В главе 4 было продемонстрировано влияние пространственного (структурного) и временного (энергетического) типов беспорядка на процесс термоокислительной деструкции в случае композиций ПЭВП + Z. Ниже мы рассмотрим структурные аспекты этих эффектов.

На рис. 5.6 и 5.7 показаны зависимости концентрации карбонильных групп [> C = 0] C_карб от продолжительности теплового старения t_ст при температурах старения Т_ст = 353 и 463 К, соответственно, для ПЭВП и двух композиций ПЭВП + Z. Как можно видеть, качественно зависимости С_карб(t_ст) для обеих использованных Т_ст симбатны и различие по существу заключается в шкале t_ст или скорости термоокислительной деструкции (сравните с рис. 4.15 и 4.16).

Рассмотрим возможное описание процесса термоокислительной деструкции в рамках фрактальных моделей [19; 20]. Как и ранее, траектория молекулы О₂ в этих моделях рассматривается как траектория случайного блуждания, а количество прореагировавших с О₂ центров макромолекул - как число посещенных этими блужданиями мест . Очевидно, в такой трактовке следует принять [17; 18]:

= C_карб.                                                          (5.2)

Далее можно записать форму зависимости  от времени t_ст [21]:

,                                                          (5.3)

по аналогии с соотношением (4.9).

С учетом соотношений (5.2) и (5.3) можно построить зависимость С_карб от t_ст в двойных логарифмических координатах и по их наклону определить величину d_s. На рис. 5.8 приведены такие зависимости для ПЭВП и двух композиций ПЭВП + Z при Т_ст = 463 К. Как можно видеть, получены ожидаемые линейные корреляции, позволяющие определить величины d_s, которые оказались равны 4,79 ¸ 7,85. Как известно [22], собственно величина d_s может варьироваться только в пределах 1 ¸ 3 и тот факт, что полученные из наклонов графиков рис. 5.8 величины d_s > 3 означает, что они являются эффективными значениями, определяемыми согласно уравнению (4.18). Расчет d_s согласно уравнению (4.29) дал среднюю величину этой размерности для всех рассматриваемых полиэтиленов ~ 1,49 [18]. Затем можно рассчитать величину показателя g_в, характеризующего степень временного (энергетического) беспорядка, согласно уравнению (1.70). Величина g_в варьируется в пределах 3,65 ¸ 7,85. Физический смысл показателя g_в заключается в следующем. Вероятность y(t) того, что некоторое следующее событие случится через промежуток времени t после предыдущего, записывается так [20]:

,                                                       (5.4)

где с - некоторая константа.

Полагая в контексте настоящего изложения, что событием является реакция молекулы О₂ с реакционноспособным центром макромолекулы полиэтилена и принимая произвольно с = 10⁴, получим, что для g_в = 3,65 промежуток времени между двумя соседними событиями равен 7,25 относительных временных единиц, а для g_в = 7,85 - 2,83 таких же единиц. Таким образом, указанная вше вариация g_в приводит к уменьшению временных промежутков между образованием карбонильных групп примерно в 2,5 раза. При указанных выше оценках величина y(t) = 1, т.е., равна достоверности события. Соотношение (5.4) показывает наличие временного скейлинга для функции y(t), т.е., ее фрактальную во времени природу [20]. Это означает, что траектория О₂ на структуре полиэтиленов должна описываться не случайным блужданием (СБ), а случайным блужданием с непрерывным временем (СБНВ), модель которого основана на введении фрактального множества времен событий [20].

Рассмотрим структурные аспекты увеличения g_в или усиления временного (энергетического) беспорядка. Алгебраическое затухание F(t) в общем случае можно описать так [20]:

, g_в > 0, t > t,                            (5.5)

где t - продолжительность реакции, t - время релаксации.

Прологарифмировав соотношение (5.5), получим, что обратная величина g_в пропорциональная lnt. В свою очередь, уравнение Дулитла дает взаимосвязь lnt и свободного объема полимера f_c [23]:

,                                                            (5.6)

где В - константа.

Величина f_c для Т_ст = 353 К может быть оценена из уравнения [23]:

,                                           (5.7)

где n_р - коэффициент Пуассона.

Для расплава ПЭВП (Т_ст = 463 К) принята величина f_c = 0,113 [24], а для композиций ПЭВП + Z величина f_c для расплава рассчитана из уравнения [25]:

,                                                       (5.8)

где h - вязкость расплава, принимаемая равной обратной величине показателя текучести расплава (ПТР) [26], а константа А определена из известных данных f_c = 0,113 и ПТР для ПЭВП [17].

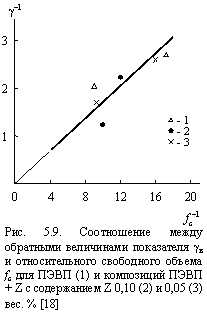
Таким образом, из сочетания уравнений (5.5) ¸ (5.8) следует линейная корреляция между g_в и f_c. Это положение подтверждается данными рис. 5.9, которые демонстрируют наличие указанной корреляции. Этот факт можно трактовать не только с позиций теории свободного объема, но и с позиций фрактального анализа. Повышение g_в по мере роста Т_ст означает усиление энергетического беспорядка структуры [27]. Как известно [28], степень энергетического возбуждения структуры полимера, а точнее - ее рыхлоупакованных областей, можно охарактеризовать с помощью размерности областей локализации избыточной энергии D_f, величина которой определяется согласно уравнению (1.25).

Сочетание уравнений (1.25) и (5.7) позволяет получить следующее соотношение между D_f и f_c [17]:

.                                     (5.9)

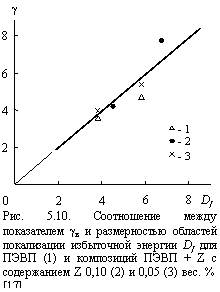
Таким образом, исходя из приведенного на рис. 5.9 соотношения между g_в и f_c, а также уравнения (5.9), следует ожидать взаимосвязи между g_в и D_f. Действительно, данные рис. 5.10 подтверждают это предположение, аналитически выражаемое так [17]:

g_в » D_f.                                                                  (5.10)

Тогда применительно к термоокислительной деструкции полиэтиленов уравнение (5.3) можно записать следующим образом [18]:

,                                   (5.11)

где C₆ - константа,  - продолжительность периода индукции.

На рис. 5.6 и 5.7 показано сравнение экспериментальных и рассчитанных по уравнению (5.11) (постоянный коэффициент в этом уравнении определен методом совмещения [17]) зависимостей с_карб(t_ст). Как можно видеть, для всех трех исследованных полиэтиленов получено хорошее соответствие теории и эксперимента, что позволяет применение рассмотренной фрактальной модели для описаний кинетики термоокислительной деструкции полиэтиленов [18].

Следовательно, изложенные выше результаты показали, что на кинетику термоокислительной деструкции в полиэтиленах оказывает влияние как пространственный (структурный), так и временной (энергетический) беспорядок. При этом выполняется теорема о субординации, т.е., наблюдается мультипликативное поведение d_s и g_в (или D_f), которые характеризуют эти типы беспорядка. Поскольку тепловое старение обычно выполняется при относительно высоких температурах, то это обстоятельство приводит к повышению роли временного (энергетического) беспорядка.

До сих пор мы рассматривали описание уровня временного (энергетического) беспорядка с помощью показателя g_в согласно уравнению (4.16) [20]. Однако, этот эффект может быть рассмотрен и в рамках модели [27; 29], где он учитывается с помощью эффективной спектральной размерности  или показателя неоднородности реакционной среды h (см. уравнения (1.68) ¸ (1.70)). По своему физическому содержанию указанные модели идентичны, что позволяет ожидать сходных зависимостей их основных параметров от структурных характеристик. Авторы [30] исследовали соотношение параметра b¢ в уравнении (1.70), характеризующего временной (энергетический) беспорядок [27], и структуры для ряда полимеров.

Поскольку процесс термоокислительной деструкции тесно связан с процессами диффузии кислорода на фрактальной структуре полимеров, а последние контролируются характеристиками свободного объема (см. главу 2), то можно ожидать взаимосвязи f_c и b¢ в уравнении (1.70). На рис. 5.11 приведена такая корреляция для пяти полимеров, из которой следует, что зависимость b¢(f_c) линейна и проходит через начало координат. Максимальная величина = 2, как следует из уравнения (1.69), и тогда максимальная величина b¢ при условии d_s = 1,33 (для разветвленного полимера [22]) равна ~ 1,50.Максимальное значение f_c при температурах выше температуры стеклования (плавления) варьируется в пределах 0,109 ¸ 0,159 для разных полимеров [31]. Соответствующие указанным предельным значениям b¢ и f_c линейные граничные зависимости b¢(f_c) показаны на рис. 5.11 штриховыми линиями. Как можно видеть, экспериментальная зависимость b¢(f_c) хорошо согласуется с указанными предельными случаями. Таким образом, данные рис. 5.11 позволяют получить следующую эмпирическую корреляцию [30]:

b¢» 10,3f_c.                                                            (5.12)

и соотношение (4.16) преобразуется к виду (вновь при условии d_s = const = 1,0) [30]:

.                                     (5.13)

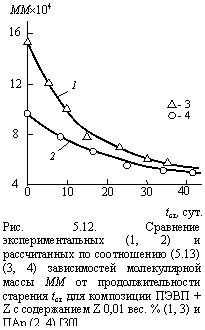
Сравнение экспериментальных и рассчитанных по уравнению (5.13) изменений ММ как функции t_ст для двух полимеров (ПАр и ПЭВП + Z с содержанием Z 0,01 вес. %) приведено на рис. 5.12, откуда следует хорошее соответствие теории и эксперимента.

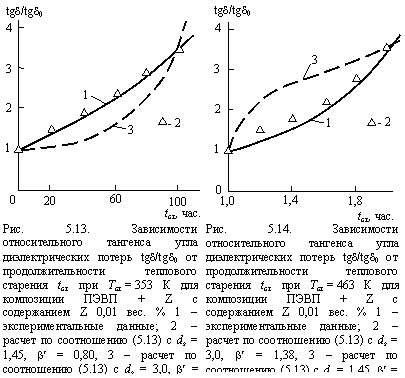
Предложенная трактовка позволяет объяснить большое (примерно на два порядка) различие интенсивностей старения полиэтилена при температурах ниже и выше его температуры плавления Т_пл (см. рис. 4.15 и 4.16, а также 5.6 и 5.7). Количественное соответствие может быть получено в рамках единой модели (соотношение (4.16) с заменой g_в d_s на ) соответствующим выбором величины . Так, при температуре старения Т_ст < Т_пл, равной 353 К, d_s = 1,45 и b¢ = 0,80 для композиции ПЭВП = Z, содержащей 0,01 вес. % Z. При Т_ст > Т_пл, равной 463 К, расплав представляет собой каучукоподобное состояние, чья структура является евклидовым (или близким к евклидовому) объектом и для ее d_s = 3 и b¢ = 1,38, как отмечалось выше. На рис. 5.13 и 5.14 приведено сравнение экспериментальных и рассчитанных по соотношению (5.13) зависимостей относительного тангенса угла диэлектрических потерь tgd/tgd₀ от продолжительности теплового старения t_ст для композиции ПЭВП + Z с содержанием Z 0,01 вес. % при Т_ст = 353 и 463 К, соответственно. Как можно видеть, несмотря на большое различие интервалов t_ст, в обоих случаях получено хорошее соответствие теории и эксперимента. Таким образом, резкое повышение интенсивности термоокислительной деструкции Т_ст > Т_пл обусловлено потерей структурой полимера фрактальных свойств [30]. Отметим, что константа с_u в соотношении (5.13) для графиков рис. 5.13 и 5.14 получена методом совмещения (как и для графиков рис. 5.12). При этом для условий Т_ст < Т_пл (рис. 513) и Т_ст > Т_пл (рис. 5.14) указанная константа имеет разные абсолютные величины. На первый взгляд может показаться, что полученное на рис. 5.13 и 5.14 хорошее соответствие теории и эксперимента может быть достигнуто только соответствующим выбором константы c_u. Для проверки этого предположения авторы [30] построили теоретические зависимости tgd/tgd₀(t_ст) с показателями соотношения (5.13) наоборот (т.е., для Т_ст < Т_пл d_s = 3, b¢ = 1,38 и для Т_ст > Т_пл d_s = 1,45, b¢ = 0,80) и соответствующими другими константами c_u. Эти зависимости показаны на рис. 5.13 и 5.14 штриховыми линиями. Как можно видеть, в таком варианте соответствия теории и эксперимента получить не удалось. Особенно это заметно для графиков рис. 5.14, где теоретическая и экспериментальные кривые tgd/tgd₀(t_ст) имеют выпуклости разного знака («вверх» и «вниз», соответственно). Следовательно, соответствие теории и эксперимента на графиках рис. 5.13 и 5.14 обусловлено корректным выбором параметром d_s и b¢ [30].

Как указано выше, в рамках фрактального анализа степень энергетического беспорядка может быть описана с помощью размерности D_f. Отметим, что именно эта размерность контролирует распределение размеров микрополостей флуктуационного свободного объема [32]. Уравнение (5.9) демонстрирует взаимосвязь параметров D_f и f_c, а сочетание уравнений (5.9) и (5.12) позволяет получить следующее соотношение между b¢ и D_f [30]:

b¢ = 0,0876 (3D_f - 4).                                        (5.14)

Уравнение (5.14) показывает увеличение b¢ по мере роста степени энергетического беспорядка, характеризуемой размерностью D_f.

Сочетание уравнений (5.10) и (5.14) также позволяет получить простое аналитическое соотношение параметров g_в и b¢, характеризующих уровень временного (энергетического) беспорядка системы:

g_в » 5,14b¢,                                                          (5.15)

что подтверждает постулированную выше аналогию моделей [20] и [27; 29]. Используя цитированный выше интервал величин g_в = 3,65 ¸ 7,85 [17; 18] и уравнение (5.15), можно оценить соответствующий интервал значений b¢ как 0,71 ¸ 1,53, что является разумной вариацией этого параметра.

Связь параметра b¢ с уровнем временного беспорядка можно продемонстрировать следующим образом. При определенном типе распределения плотности энергетических состояний показатель b¢ определяется так [20]:

,                                (5.16)

где Т₀ - характеристическая температура, описывающая спад плотности энергетических состояний.

Таблица 5.1

Сравнение температур переходов и характеристических температур для ПК и ПАр [30]

Полимер	Т0, К	Тс¢, К	Ткр, К	Tll, К
ПК	369	373	509	508
ПАр	411	423	567	568

Из данных рис. 5.11 следует, что для ПК и ПАр коэффициент в уравнении (5.12) несколько меньше средней величины 10,3 и равен ~ 9. Тогда из уравнения (5.12) для b¢ = 1 получим f_c » 0,111. На рис. 5.15 показаны зависимости f_c(T) для ПК и ПАр, из которых можно оценить температуру Т₀, соответствующую условию f_c = 0,111 (или b¢ = 1). Эти величины Т₀ приведены в табл. 5.1. Как известно [12], теория двухстадийного стеклования полимеров предполагает, что при некоторой температуре ( < T_c) происходит распад нестабильных кластеров, удерживающих рыхлоупакованную матрицу в стеклообразном состоянии, что определяет ее расстекловывание. Обычно принимается следующее приближенное соотношение между Т_с¢ и Т_с [33]:

Т_с¢ = Т_с - 50 К.                                                    (5.17)

Оцененные таким образом величины Т_с¢ приведены в табл. 5.1, откуда следует их близкое соответствие величина Т₀. Далее оценим температуру Т_кр, при которой величина b¢ достигает своего максимального значения 1,38, что также можно сделать согласно уравнению (5.16). Одним из важнейших переходов в неупорядоченной структуре полимеров следует считать так называемый переход «жидкость 1 - жидкость 2» или T_ll - переход, проявляющийся выше Т_с [34]. Это название дано Бойером и оно указывает на превращение «жидкости с фиксированной структурой» в истинно жидкое состояние. Переход T_ll по существу определяет физическую границу между высокоэластическим и вязкотекучим состояниями полимера. Величину T_ll можно оценить согласно уравнению (1.43). Сравнение рассчитанных указанным образом величин Т_кр и T_ll также приведено в табл. 5.1, из которого следует практическое равенство указанных температур. Данные табл. 5.1 дают возможность прогнозировать b¢ простейшим способом (по крайней мере, для аморфных полимеров, где определение температур и T_ll наиболее просто): по двум точкам (b = 1 при  и b = 1,38 при T_ll) строится калибровочная прямая и по ней определяется величина b¢ при произвольной температуре теплового старения Т_ст [30].

На рис. 5.16 показано сравнение величин b¢ (расчет по уравнению (5.12)) и Т/Т₀ для ПК и ПАр. Как можно видеть, получено приблизительное равенство этих параметров, что подтверждает сделанное выше предположение: величина b¢ определяется уровнем временного (энергетического) беспорядка системы [30].

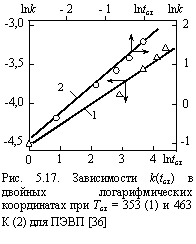
Авторы [36] использовали модель [27; 29] для количественной оценки степени влияния пространственного и временного беспорядка на скорость термоокислительной деструкции ПЭВП. Для экспериментального определения показателя неоднородности h согласно уравнению (1.68) была определена скорость изменения k относительного тангенса угла диэлектрических потерь tgd/tgd₀ (см. рис. 4.15 и 4.16) как функция k(t_ст). На рис. 5.17 приведены зависимости k(t_ст) в двойных логарифмических координатах, которые позволяют определить величину h из наклона линейных графиков согласно уравнению (1.69). Эти значения приведены в табл. 5.2, откуда следует их существенное различие: Т_ст = 353 и 463 К. Если для Т_ст = 353 К величина h относительно невелика и близка к соответствующей величине для евклидовых (гомогенных) сред, то при Т_ст = 463 К этот показатель близок к величине для полностью неупорядоченных сред. Далее можно рассчитать величину   согласно уравнению (1.69) для обеих Т_ст, которые также приведены в табл. 5.2. Переход от аморфно-кристаллического состояния (Т_ст = 353 К) к расплаву (Т_ст = 463 К) приводит к резкому снижению , обусловленному ростом степени гетерогенности последнего. Расчет спектральной размерности d_s, характеризующей связность объекта, для твердофазного полимера можно выполнить согласно уравнению (4.29) и тогда d_s = 1,46, т.е., практически точно совпадает с величиной . Это указывает, что при Т_ст = 353 К, т.е., при Т_ст < Т_пл, процесс термоокислительной деструкции контролируется только пространственным (структурным) беспорядком. Для расплава d_s можно принять равной соответствующей размерности для линейной макромолекулы, т.е., d_s = 1,0 [22], а структурную величину  ( )можно оценить из уравнения (1.72). Тогда  = 0,96 и близка к принятой выше d_s (табл. 5.2). Определить величину h, соответствующую пространственному беспорядку в расплаве, можно из уравнения (1.69) при условии  = (h = 0,520).

Таблица 5.2

Сравнение характеристик термооокислительной деструкции ПЭВП ниже (353 К) и выше (463 К)

температуры плавления [36]

Тст, К	h		ds		nпр	nвр	n
353	0,263	1,47	1,46	1,46	2,36	1,0	2,36
463	0,905	0,19	1,0	0,96	3,08	3,47	11,49

Как показано в работе [37], порядок реакции n связан с показателем h следующим уравнением:

.                                                        (5.18)

Расчет порядка реакции n_пр, обусловленного пространственным беспорядком, согласно уравнению (5.18) при h = 0,293 Т_ст = 353 К и h = 0,520 согласно уравнению (1.69) и условию  =   для Т_ст = 463 К показал, что эти значения n_пр равны 2,36 и 3,08, соответственно. Иначе говоря, повышение степени пространственного беспорядка, характеризуемое увеличением h от 0,263 до 0,520, приводит к росту n_пр от 2,36 при Т_ст = 353 К до 3,08 при Т_ст = 463 К. Поскольку при Т_ст = 353 К  = d_s, т.е., временной беспорядок отсутствует, то общий порядок реакции n равен пространственному: n = n_пр. Для второй из указанных температур теплового старения d_s = 1 и = 0,19, т.е., d_s ≠ , и величина n, рассчитанная согласно уравнению (5.18), равна 11,49. Отметим, что отношение величин n для Т_ст = 353 и 463 К равно 4,88, т.е., примерно 5, что соответствует приведенным выше данным [38] (см. главу 4). Очевидно, что при Т_ст > Т_пл порядок реакции n контролируется как пространственным (n_пр), так и временным (n_вр) беспорядком, что соответствует известным данным [27] и определяется теоремой о субординации [20]:

N = n_прn_вр.                                                            (5.19)

Из уравнения (5.19) следует n_вр = 3,73, т.е., временной беспорядок оказывает даже большее влияние на величину n при Т_ст = 463 К, чем пространственный [36].