
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.3. Понятие о простой поверхности
Интуитивно простую поверхность можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям).
Более строго, простой поверхностью называется образ гомеоморфного[2] отображения (то есть взаимно однозначного и взаимно непрерывного отображения) внутренности единичного квадрата. Этому определению можно дать аналитическое выражение. Пример простой поверхности приведён на рис. 7.2.
Пусть на плоскости с прямоугольной системой координат u и v задан квадрат, координаты внутренних точек которого удовлетворяют следующим неравенствам 0< u < 1, 0 < v < 1.
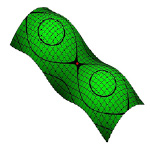
Рис. 7.2. Простая поверхность
Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул
х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u’, v’) были различными соответствующие точки (x, у, z) и (x’, у’, z’).
Примером простой поверхности является полусфера. Вся же сфера не является простой поверхностью. Это вызывает необходимость дальнейшего обобщения понятия поверхности.
Подмножество пространства, у каждой точки которого есть окрестность, являющаяся простой поверхностью, называется правильной поверхностью.
Поверхности могут быть кривыми и иметь параметр кривизны.
Для разных направлений в заданной точке поверхности получается разная кривизна нормального сечения, которая называется нормальной кривизной.
Нормальной кривизне приписывается знак плюс, если главная нормаль кривой идёт в том же направлении, что и нормаль к поверхности, или минус, если направления нормалей противоположны (рис. 7.3).
Вообще говоря, в каждой точке поверхности существуют два перпендикулярных направления e1 и e2, в которых нормальная кривизна принимает минимальное и максимальное значения; эти направления называются главными.
Исключение составляет случай, когда нормальная кривизна по всем направлениям одинакова (например, у сферы или на торце эллипсоида вращения), тогда все направления в точке – главные.
Нормальные кривизны в главных направлениях называются главными кривизнами; обозначим их k1 и k2.
Величина: K = k1 k2 называется гауссовой кривизной[3], полной кривизной или просто кривизной поверхности.
Встречается также термин скаляр кривизны, который подразумевает результат свёртки тензора[4] кривизны; при этом скаляр кривизны вдвое больше, чем гауссова кривизна.
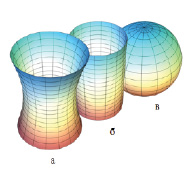
Рис.7.3. Поверхности с кривизной:
а – отрицательной; б – нулевой; в – положительной
Гауссова кривизна может быть вычислена через метрику, и поэтому она является объектом внутренней геометрии поверхностей (отметим, что главные кривизны к внутренней геометрии не относятся).
По знаку кривизны можно классифицировать точки поверхности (см. рисунок).
Кривизна плоскости равна нулю.
Кривизна сферы радиуса R всюду равна К=1/R2 .
Существует поверхность постоянной отрицательной кривизны – псевдосфера.
