
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
9.3. Построение развертки пирамиды способом триангуляции
Боковые грани любой пирамиды являются треугольниками. Для построения развертки пирамиды (рис. 9.3) необходимо предварительно определить натуральные величины боковых ребер и сторон основания.
У изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П1в истинную величину. Истинные величины боковых ребер определены способом прямоугольных треугольников S2M0C0, S2M0B0 и S2M0А0, у которых одним катетом является высота пирамиды (S2М0 – разность высот точки S и точек А, В, С), а другим – горизонтальная проекция соответствующего ребра.
(/M0C0/ = /S1C1/; /M0B0/ = /S1B1/; /M0A0/ = /S1A1/; /M0K0/ = /S1K1/).
Натуральные величины ребер пирамиды могут быть определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П1.
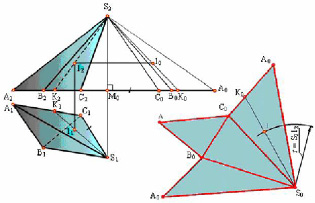
Рис. 9.3. Построение развертки пирамиды
Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание (ΔАВС), получим полную развертку пирамиды. Построение на развертке точки 1, принадлежащей поверхности пирамиды, понятно из чертежа. Такой способ построения развертки поверхности называется способом триангуляций.
