Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

5.3. Фрактальная кинетика термоокислительной деструкции полимеров

Структура твердофазных полимеров представляет собой фрактальный объект в интервале линейных масштабов от нескольких ангстрем до нескольких десятков ангстрем и может моделироваться как совокупность большого числа кластеров Виттена-Сандера (кластеров WS) [39; 40]. Авторы [41] использовали эту структурную модель для описания термоокислительной деструкции ПАр ниже Т_с и влияния указанного процесса на конечные свойства полимера.

На рис. 5.18 показана зависимость характеристической вязкости [h] от продолжительности теплового старения t_ст для образцов ПАр. Авторы [41] предположили, что основным результатом термоокислительной деструкции является снижение молекулярной массы или [h] ПАр в процессе старения и это снижение определяет изменение свойств полимера. Обращает на себя внимание нелинейность зависимости [h](t_ст), которая означает уменьшение скорости термоокислительной деструкции k по мере роста t_ст, что является, как отмечалось выше, типичным фрактальным поведением. В этом случае величину k можно определить следующим образом [41]:

,                                                  (5.20)

где [h]₀ - характеристическая вязкость исходного образца ПАр; [h]_i - характеристическая вязкость образца ПАр после i-го промежутка старения, t_стi - время старения, соответствующее окончанию i-го промежутка.

На рис. 5.19 показана зависимость k(t_ст) в двойных логарифмических координатах, соответствующая соотношению (1.68). Как следует из этого графика, указанная зависимость хорошо аппроксимируется прямой, что позволяет рассчитать величину k по мере роста t_ст однозначно указывает на фрактальную кинетику термоокислительной деструкции в твердофазном состоянии ПАр. Такое поведение ожидалось в силу фрактальности структуры ПАр. Расчет эффективной спектральной размерности   согласно уравнению (1.69) дает величину   = 1,578, что близко к величине d_s для аморфных стеклообразных полимеров [42; 43]. В свою очередь, это предполагает близкую к единице величину b¢. Указанное обстоятельство, а также относительно небольшая величина h, означает, что в процессе старения при относительно высоких (близких к температуре стеклования) температурах фракталоподобные эффекты связаны с пространственным (структурным) беспорядком [27].

В рамках рассмотренной модели можно проследить изменение свойств ПАр в процессе теплового старения в предположении, что единственным механизмом теплового старения является термоокислительная деструкция, приводящая к снижению молекулярной массы полимера [41]. В этом случае следует предположить, что критическая скорость освобождения энергии деформации G_Ic, которая служит показателем пластичности полимера [44], изменяется симбатно [h] [45]. Тогда по аналогии с уравнением (5.20) можно записать [41]:

,                                                    (5.21)

где  - пластичность исходного образца ПАр; - пластичность образцов ПАр после i-го промежутка старения t_стi.

На рис. 5.20 приведено сравнение экспериментального изменения G_Ic со временем старения t_ст и теоретических зависимостей G_Ic(t_ст), соответствующих классическому (кривая 1) и фрактальному (кривая 2) поведению. Из этого сравнения видно, что экспериментальная зависимость G_Ic(t_ст) согласуется с фрактальным поведением, а в случае классического поведения (h = 0,  = 2,0) старение протекает гораздо быстрее. Кроме того, на рис. 5.20 приведена зависимость G_Ic(t_ст), для случая h = 0,4 или  = 1,20. Как можно видеть, уменьшение от 1,578 до 1,20 повышает стойкость ПАр к воздействию теплового старения, что особенно наглядно в области больших t_ст. Далее авторы [41] рассчитали величину t_ст, при которой значение G_ic = 0. Эта ситуация соответствует такому уровню термоокислительной деструкции, при котором молекулярная масса полимера снижается настолько, что в нем уже не образуется сетка макромолекулярных зацеплений и полимер становится предельно хрупким [46]. Это значение t_ст равно ~ 720 час. в случае классическое поведения, ~ 1100 час. в случае фрактального поведения при  = 1,578 и ~ 1900 час. при  = 1,20 [41]. Таким образом, фрактальность структуры полимера приводит к ослаблению эффектов термоокислительной деструкции по сравнению с гипотетическим полимером, чья структура является евклидовым объектом. Предложенный в работе [41] подход позволяет прогнозирование вариации пластичности (или других свойств) полимера в процессе теплового старения, основным механизмом которого является термоокислительная деструкция.

В работе [13] рассмотрена теоретическая трактовка процессов переноса и реакций на кластерах WS. В рамках этой трактовки получено соотношение для средней вероятности выживания случайного блуждания F(t) после времени t (соотношение (4.16)), которое использовано авторами [47; 48] для g_в = 1. Рассмотрим применение этой модели, физический смысл и определение входящих в него параметров применительно к реакции термоокислительной деструкции в твердофазных полимерах. Авторы [47; 48] рассматривали структуру аморфного полимера (или структуру аморфной фазы аморфно-кристаллического полимера) как совокупность кластеров WS [39; 40], а молекулы кислорода - как частицы, совершающие случайное блуждание на этом фрактальном объекте. В такой трактовке «выживание» частицы (молекулы О₂) означает ее неучастие в процессе термоокислительной деструкции и, следовательно, чем меньше F(t), тем больше частиц (молекул кислорода) приняло участие в процессе деструкции и тем ниже конечная молекулярная масса (ММ) полимера, подвергнутого тепловому старению. Иначе говоря, авторы [47; 48] предположили, что единственным механизмом теплового старения является термоокислительная деструкция, а единственным ее результатом - снижение ММ полимера. Тогда экспериментальные значения вероятности выживания F(t)^э можно оценить так [47]:

,                                                   (5.22)

где MM_i - молекулярная масса образца после i-го промежутка старения t_стi, ММ₀ - молекулярная масса исходного образца при t_ст = 0.

Для кластера WS фрактальная размерность структуры d_f » 2,5 [49], для структуры различных полимеров d_f » 2,6 ¸ 2,7 [28]. Это дает интервал величин d_s для ПАр и композиции ПЭВП + Z с содержанием Z 0,01 вес. %, использованных в работах [47; 48], ~ 1,43 ¸ 1,46 согласно уравнению (4.29), что хорошо согласуется с результатами компьютерного моделирования [49] и экспериментальными оценками [42; 43; 50]. Однако, поскольку тепловое старение протекает при относительно высоких температурах (близких к температуре стеклования или плавления полимеров), то это обстоятельство может изменить величину d_s вследствие наличия временного беспорядка [27]. Как отмечалось выше, для ПАр = 1,578, а для ПЭВП + Z согласно уравнению (1.69) получена величина  = 1,07. Таким образом, если для ПАр, наблюдается примерное равенство d_s и , то для ПЭВП + Z расхождение этих параметров довольно велико. Это соответствует теореме о субординации [27] или уравнению (1.70), из которого для ПЭВП + Z b¢ = 0,74. Таким образом, введение Z в ПЭВП приводит к уменьшению временного беспорядка или величины b¢. В рамках задачи о ловушках [13] это означает, что частицы Z, поглощая молекулы кислорода, прерывают их траектории, снижая тем самым эффективную степень связности структуры, характеризуемую размерностью . Следовательно, приведенный пример вновь показывает, что использование размерности d_s, не учитывающей температурных и/или структурных изменений b¢, может привести к существенным погрешностям.

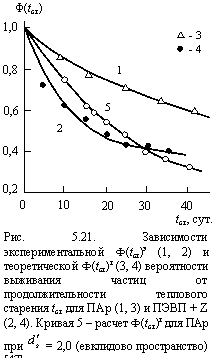
Теперь, используя соотношение (4.16) при g_в = 1, в котором константа с_u определялась по принципу наилучшего совмещения, и указанные выше значения , можно рассчитать теоретические значения F(t_ст)^т и сравнить их с оценкой F(t_ст)^э согласно уравнению (5.22). Такое сравнение для ПАр и ПЭВП + Z приведено на рис. 5.21, из которого следует хорошее соответствие теории и эксперимента.

Далее рассмотрим влияние типа пространства (фрактальное или евклидово), в котором протекает термоокислительная деструкция. Для евклидова пространства = 2,0, как отмечалось выше. Оценка F(t_ст)^т для этого случая также приведена для ПАр на рис. 5.21 (кривая 5) и сравнение кривых F(t_ст)^т при  = 1,578 (фрактальное пространство) и =2,0 (евклидово пространство) показывает, что в последнем случае снижение F(t_ст)^т или снижение ММ протекает примерно в два раза быстрее, чем в первом, что и ожидалось из самых общих соображений [19; 20; 29].

В главах 4 и 5 были рассмотрены химические механизмы и структурные аспекты термоокислительной деструкции ПБТФ. Дополнительную информацию об этих процессах можно получить исследованием их кинетики [51; 52].

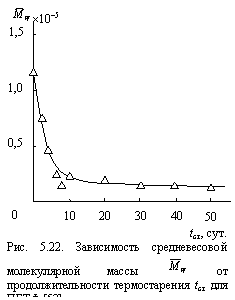
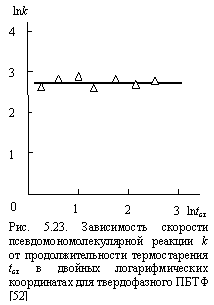
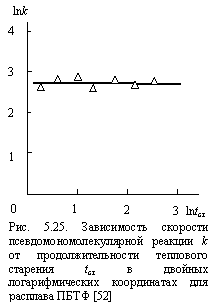
На рис. 5.22 приведена зависимость средневесовой молекулярной массы  от продолжительности теплового старения t_ст при Т_ст = 393 К для ПБТФ, из которой следует быстрый спад  в течение примерно первых десяти суток, а затем этот спад резко замедляется. Как и ранее, скорость термоокислительной деструкции k может быть описана соотношением (1.68). Зависимость k(t_ст) в двойных логарифмических координатах согласно соотношению (1.68) позволяет определить величину показателя неоднородности h. На рис. 5.23 и 5.24 приведены такие зависимости для участков псевдомоно- и бимолекулярной реакций термоокислительной деструкции ПБТФ, соответственно. В первом случае (рис. 5.23) скорость реакции k не зависит от t_ст, т.е., в этом случае получено классическое поведение (протекание реакции в евклидовом пространстве), где k = const и h = 0. Поскольку в случае полимеров евклидовым объектом может быть только расстеклованный (каучукоподобный) полимер [28], то полученные результаты подтверждают вывод работ [9; 10] о протекании псевдомономолекулярной реакции в процессе термоокислительной деструкции ПБТФ в расстеклованных областях аморфной фазы. Для сравнения на рис. 5.25 приведена зависимость k(t_ст) для теплового старения ПБТФ выше температуры его плавления, т.е., для его расплава. В этом случае весь образец представляет собой евклидов объект [28] и, как и следовало ожидать, для него также получено k = const, h = 0 (классическое поведение). Таким образом, принципиальных различий протекания псевдомономолекулярной реакции для расстеклованных областей аморфной фазы твердофазного ПБТФ (при Т_с < Т_ст < Т_пл) и полностью расстеклованного ПБТФ (расплава) нет, поскольку указанные структурные области являются евклидовыми объектами. Однако. Скорость псевдомономолекулярной реакции в расплаве примерно в 20 раз выше, чем для твердофазного полимера. Это различие будет рассмотрено ниже.

На рис. 5.24 приведена зависимость k(t_ст) в двойных логарифмических координатах для участка реализации бимолекулярной реакции термоокислительной деструкции ПБТФ (второй участок зависимости (t_ст) на рис. 5.22). Как можно видеть, в этом случае наблюдается спад k по мере роста t_ст, что является доказательством протекания бимолекулярной реакции во фрактальном пространстве [27; 29]. Линейность этой зависимости позволяет определить показатель неоднородности h из ее наклона согласно соотношению (1.68), который равен ~ 1,0. Как показано в работах [27; 29], в этом случае = 0, т.е., бимолекулярная реакция протекает в нуль-мерном пространстве или, по определению авторов [29], в миникластерах. Такими миникластерами для аморфно-кристаллических полимеров являются плотноупакованные области (кластеры и кристаллиты) [12],что также подтверждает вывод работ [9; 10] о протекании бимолекулярной реакции в плотноупакованных областях ПБТФ. Можно видеть, что псевдомоно- и бимолекулярные реакции представляют собой предельные случаи кинетики термоокислительной деструкции, соответствующие граничным значениям h = 0 и h = 1,0 [27; 29]. Исходя из этого, следует предположить, что полученные для указанных реакций значения k дают предельные (максимальную и минимальную, соответственно) скорости термоокислительной деструкции [51; 52].

Как отмечалось выше, для ПАр получено значение h = 0,211. Это означает, что термоокислительная деструкция ПАр протекает во фрактальном пространстве, что и следовало ожидать, поскольку тепловое старение ПАр было выполнено при Т_ст < T_c [41]. Величина h для ПАр является промежуточной в интервале возможных значений 0 £ h £ 1, и это обстоятельство предполагает одновременное протекание термоокислительной деструкции как в рыхлоупакованных, так и плотноупакованных (кластерах) областях структуры ПАр. Относительно небольшие значения h для ПАр позволяют предположить, что основные деструктивные процессы реализуются в рыхлоупакованных областях структуры этого полимера [51; 52].

Таким образом, изложенные выше результаты показали, что исследование кинетики термоокислительной деструкции ПБТФ в рамках модели [27; 29] позволяет точную идентификацию структурных областей, в которых реализуются псевдомоно- и бимолекулярная реакции. Основным показателем для реализации указанных реакций является тип пространства: в евклидовом пространстве протекает псевдомономолекулярная реакция, а во фрактальном - бимолекулярная реакция [51].